G 3.2 Приклад розв’язку індивідуального завдання 4
Застосовуючи метод представлення розв’язку у вигляді ряду за власними функціями, у півсмузі , вирішити наступну крайову задачу:
;
(3.2.1)
;
(3.2.2)
.
(3.2.3)
Розв’язок.
Оскільки рівняння (3.2.1) неоднорідне, а граничні умови (3.2.2) однорідні, використовуємо метод представлення розв’язку у вигляді:
,
(3.2.4)
де — власна функція відповідної однорідної задачі:
рішення якої
визначається методом Фур'є:
(див. п.2.4), і для функції
одержуємо таку наведену задачу
Штурма-Ліувілля:
(3.2.5)
Розв’язком задачі (3.2.5) є функція:
.
(3.2.6)
Розкладемо функцію
,
що входить у диференціальне рівняння
(3.2.1), у ряд:
.
(3.2.7)
Підставляючи в
(3.2.7) аналітичні вирази для
,
,
отримуємо:
;
(3.2.8)
Підставивши розклад (3.2.4), (3.2.7) у диференціальне рівняння (3.2.1) одержуємо, відповідно до (3.1.8), диференціальне рівняння для визначення функцій :
.
(3.2.9)
Функції
визначаються відповідно до (3.2.8), тому
для
одержуємо однорідне рівняння:
,
що має очевидний тривіальний розв’язок
:
(3.2.10)
Для випадку
одержуємо відповідно до (3.2.8), (3.2.9)
диференціальне рівняння:
. (3.2.11)
Розв'язок рівняння (3.2.11) може бути поданий у вигляді:
,
(3.2.12)
де
—
загальний розв’язок відповідного
однорідного рівняння;
— частинний розв’язок рівняння
(3.2.12), обумовлений виглядом правої
частини:
.
Отже, відповідно до (3.2.12), знаходимо
. (3.2.13)
Підставляючи отримані вирази для функцій , відповідно до (3.2.13), (3.2.10), у розкладання (3.2.4), отримуємо розв’язок задачі (3.2.1) — (3.2.3) у вигляді:
. (3.2.14)
Визначимо невизначену
сталу
,
використовуючи початкову умову (3.2.3):
,
отже
.
Підставляючи знайдене значення у вираз (3.2.14) одержуємо остаточний розв’язок вихідної задачі (3.2.1)-(3.2.3):
.
? 3.3 Варіанти індивідуального завдання 4
Застосовуючи метод представлення розв’язку у вигляді ряду за власними функціями, у півсмузі , вирішити крайову задачу для рівняння теплопровідності:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
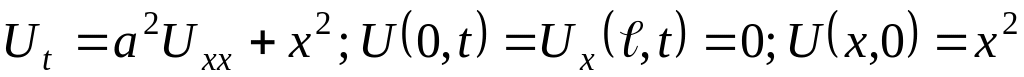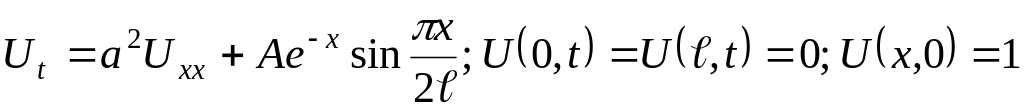3.4 Метод Дюамеля щодо розв’язку неоднорідних крайових задач математичної фізики
Для розв’язку неоднорідної крайової задачі з неоднорідним рівнянням (будь — якого типу) та однорідними граничними й початковими умовами, окрім наведеного методу представлення розв’язку у вигляді ряду за власними функціями, застосовують також метод Дюамеля, який дозволяє звести неоднорідну крайову задачу до відповідної однорідної.
Теорема.
Якщо функція
є розв’язком однорідної крайової задачі
то функція
є розв’язком такої неоднорідної крайової задачі:
