
1-14_Статистика (По дисциплине "Статистика". Контрольная работа №1,вариант №14
.).docФедеральное агентство образования.
Томский государственный университет систем управления и радиотехники.
ТУСУР
Кафедра: Экономика и управление.
Контрольная работа №1.
По дисциплине «Статистика».
Вариант №14.
Задание 1.
На основе данных о проценте ставок по межбанковским кредитам, изменяющимся по торговым дням, приведенных ниже, определить:
-
Простую среднюю арифметическую, медиану, дисперсию, размах вариации.
-
Средний уровень ряда, средний абсолютный прирост, средний темп роста, средний темп прироста.
-
Представить ряд графически в виде линейной диаграммы, определить основную тенденцию развития динамического ряда.
Значения процента ставок по межбанковским кредитам по торговым дням, представлены в виде таблицы:
|
Торговый день |
||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
28,00 |
30,57 |
30,80 |
31,33 |
31,43 |
32,33 |
32,71 |
33,00 |
33,67 |
Решение:
1.
Простая средняя арифметическая
определяется:
![]() ;
;
![]() .
.
Для определения медианы необходимо представить ряд в виде упорядоченной последовательности значений:
|
28,00 |
30,57 |
30,80 |
31,33 |
31,43 |
32,33 |
32,71 |
33,00 |
33,67 |
Медиана- величина признака, которая делит упорядоченную последовательность значений на две равные по численности части. Следовательно, Ме =31,43.
Дисперсию
определяем по формуле:
![]() ;
;
![]()
![]()
Размах вариации - это разница между максимальным и минимальным значениями. Следовательно:
H=33,67-28,00=5,67
2. Средний уровень ряда равен средней арифметической:
![]()
Определяем средний абсолютный прирост:
![]()
![]()
Средний темп роста определяется:
![]()
![]() ;
;
![]()
Средний
темп прироста
![]() ;
;
![]()
3. Построим линейную диаграмму

Проверим ряд на наличие тренда при помощи метода средних. Для этого разобьем ряд на 3 интервала, для каждого из которых определим среднее значение:

Средние, рассчитанные для каждого из интервалов, увеличиваются, следовательно, можно сделать предположение о том, что тренд является прибывающим, что и подтверждается линейной диаграммой.
Задание 2.
В таблице, приведенной ниже, представлены два ряда данных. Требуется:
-
Построить корреляционное поле
-
Определить линейный коэффициент корреляции
-
Определить уравнение теоретической линии регрессии и построить.
|
X |
27 |
35 |
29 |
25 |
27 |
31 |
29 |
21 |
23 |
|
Y |
32,56 |
30,57 |
30,80 |
31,33 |
31,43 |
32,33 |
32,71 |
33,00 |
33,67 |
Решение:
Корреляционное поле для исходных данных выглядит следующим образом:
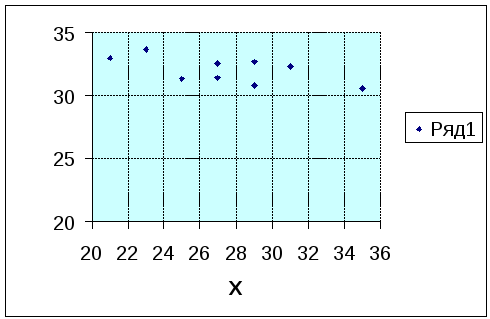
Определим линейный коэффициент корреляции:
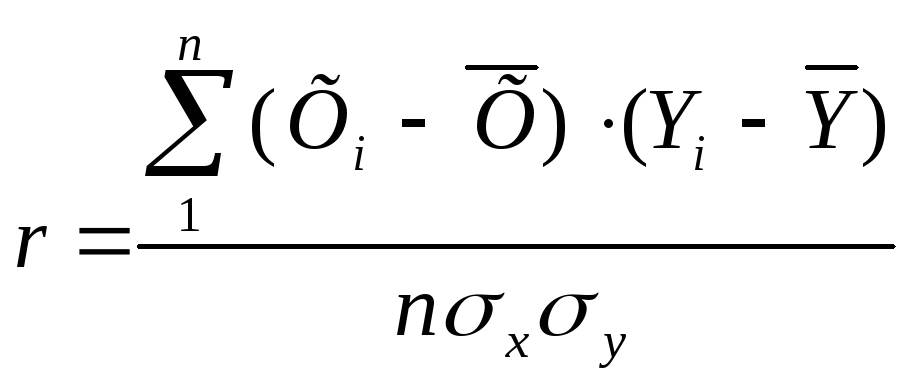

Определим теоретическую линию регрессии
![]()
методом наименьших квадратов.
![]()
Это требование выполняется при:

Подставляя данные получаем:
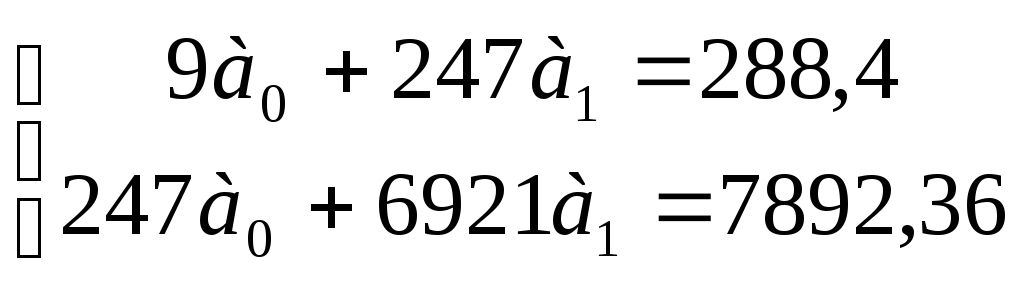
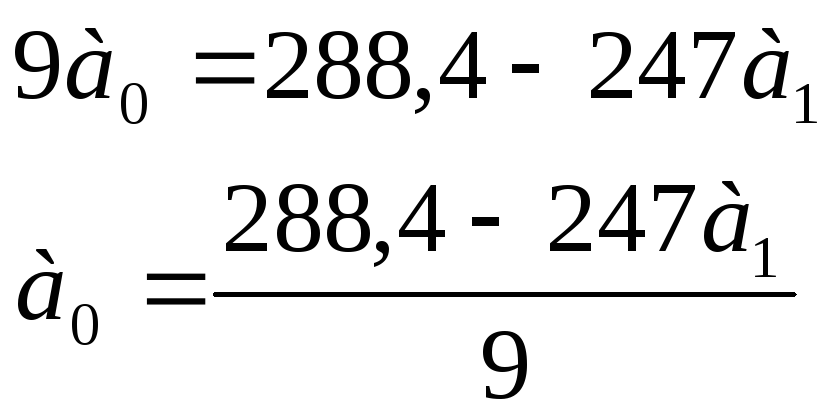
Подставляем эти данные во второе уравнение:

Теперь
подставим а1
в![]() , получим: а0=27,68.
, получим: а0=27,68.
Отсюда:
![]()
Представляем графически корреляционное поле и теоретическую линию регрессии.
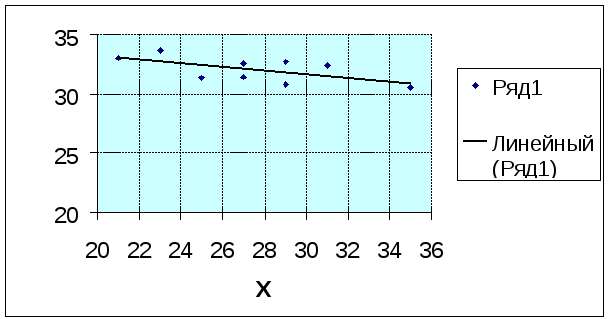
Задание 3.
По данным варианта рассчитать:
-
Индивидуальные и общий индекс цен;
-
Индивидуальные и общий индексы физического объема товарооборота;
-
Индивидуальные и общие индексы товарооборота.
|
№ Предприятия |
Базисный год |
Отчетный год |
||
|
|
Цена |
Количество |
Цена |
Количество |
|
6 |
59 |
120 |
4,6 |
169 |
|
8 |
5,7 |
130 |
6,9 |
103 |
|
9 |
6,7 |
92 |
5,2 |
136 |
Решение:
Индекс – это показатель сравнения двух состояний одного и того же явления (простого или сложного, состоящего из соизмеримых или несоизмеримых элементов); включает 2 вида:
Отчетные, оцениваемые данные ("1")
Базисные, используемые в качестве базы сравнения ("0")
Найдем индивидуальные индексы по формулам:
-
индивидуальные индексы:
![]() ;
; ![]() ;
; ![]()
-
для величины p (цены) по каждому предприятию:
![]()
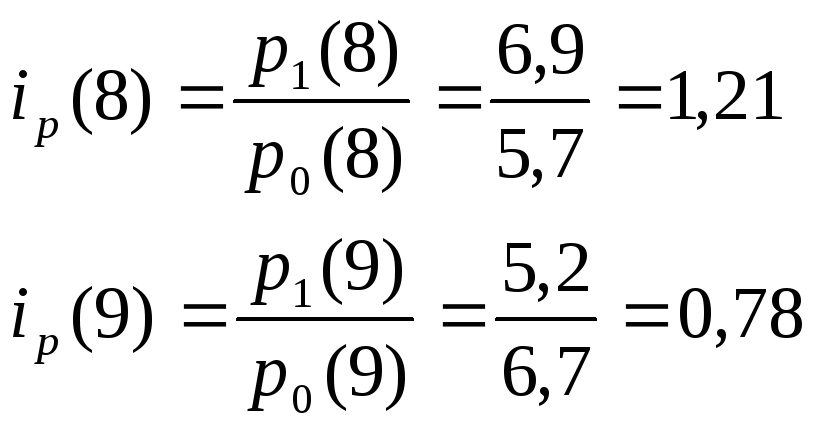
-
для величины q (объема) по каждому виду товаров:
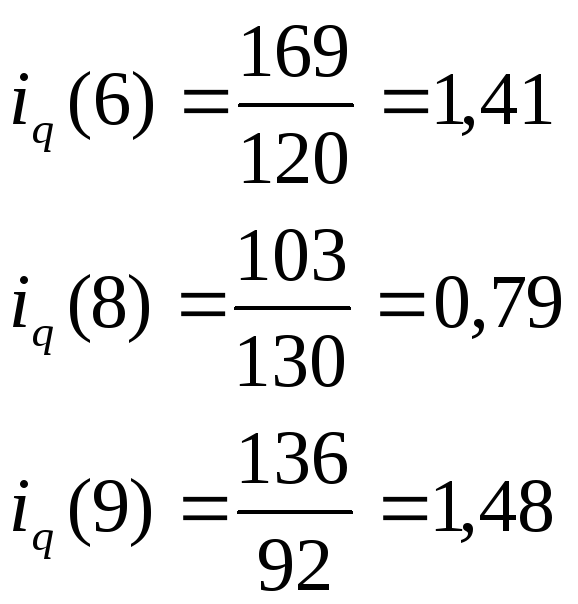
-
для общего объема товарооборота Q:
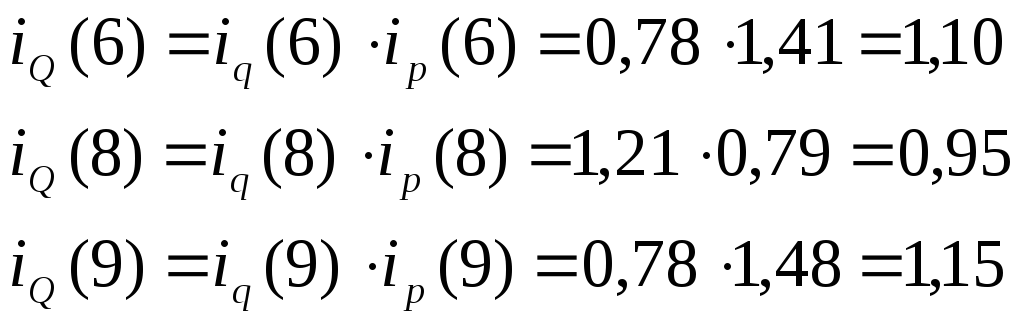
-
Найдем общие индексы (в агрегатной форме):
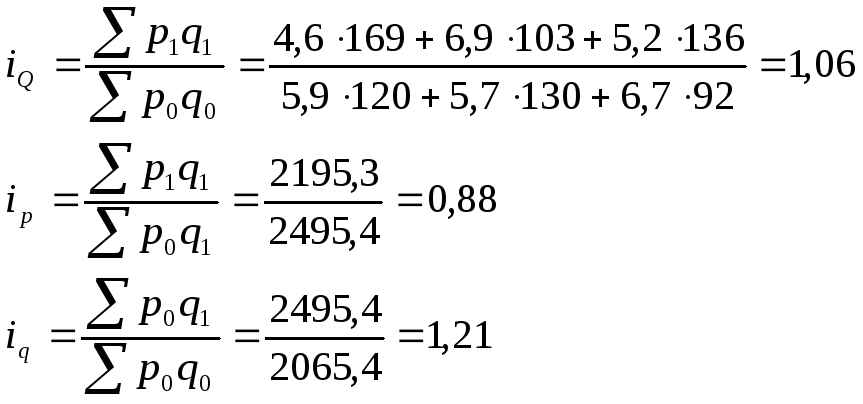
Можно сделать вывод, что увеличение общего объема товарооборота произошло из-за уменьшения цены и увеличения количества продаж (физический объем товарооборота). Оба этих фактора повлияли на прирост товарооборота.
Задание 4.
По данным рассчитать индексы сезонности, построить график сезонности и сделать выводы.
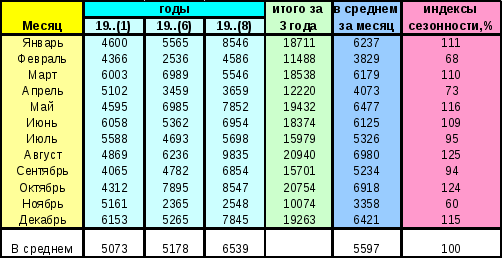
Сезонными колебаниями называют устойчивые внутригодовые колебания в ряду динамики. Они характеризуются индексами сезонности, совокупность которых на графике образует сезонную волну.
Воспользуемся следующей формулой расчета индексов сезонности:
![]()
Теперь на основании полученных индексов сезонности построим график сезонности:
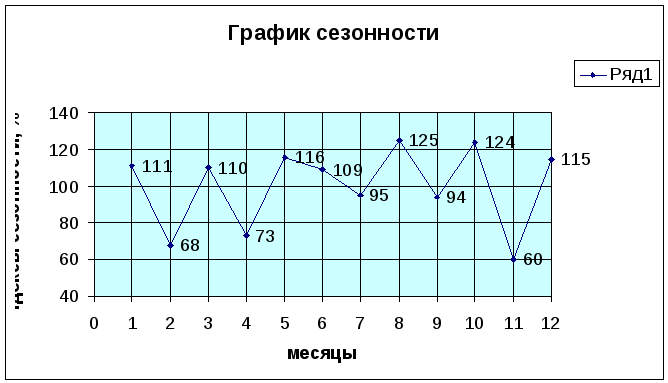
Вывод:
Сезонность в течении года имела несколько подъемов:
-
Главный – в августе (125%)
-
Второй (слабее) – в октябре (124%)
-
Наименьшие – в январе (111%); в марте (110%); в мае (116%); в декабре (115%)
Значительные уменьшения наблюдается:
-
В первом квартале – в феврале (68%)
-
Во втором квартале – в апреле (73%)
-
В третьем квартале – в июле (95%) и в сентябре (94%)
-
В четвертом квартале – в ноябре (60%)
Задание 5.
Рассчитать эффект от внедрения новой техники по данным, приведенным в таблице:
Исходные данные:
|
Капитальные вложения, тыс. руб. |
Виды продукции |
До внедрения новой техники |
После внедрения новой техники |
||||
|
Себесто-имость, руб. |
Цена, руб. |
Количество, шт. |
Себесто-имость, руб. |
Цена, руб. |
Количество, шт. |
||
|
200 |
1 |
125 |
135 |
5100 |
120 |
140 |
5000 |
|
|
2 |
450 |
455 |
630 |
440 |
455 |
650 |
Решение:
-
Определим прирост прибыли от выпуска и использования новой техники:
![]()
Для продукции 1:
![]()
Для продукции 2:
![]()
Этот прирост произошел из – за снижения себестоимости и увеличения выпуска продукции. Снижение цены на продукцию 2, однако, привело к некоторому уменьшению прибыли.
-
Снижение себестоимости от использования новой техники:
![]()
Для продукции 1:
![]()
Для продукции 2:
![]()
-
Сводный эффект от выпуска и использования новой техники:
![]()
Э = (49+6,6) – 0,15 • 200 = 25 тыс. 600 руб.
