5. Скалярное, векторное, смешанное произведения векторов

5.1. Скалярное произведение векторов

Скалярным произведением двух векторов a и b называется число, равное произведению длин этих векторов на косинус угла между ними. Обозначается (a,b) или a b. Итак, по определению:

(a,b)=abcos(a ^b) (5.1)

Если известны координаты векторов a=(x₁,y₁,z₁) и b=(x₂,y₂,z₂), то

(a,b)=x₁x₂+y₁y₂+z₁z₂ (5.2)

С помощью скалярного произведения можно вычислить угол между векторами:

cos (a ^b) = = (5.3)

Условие ортогональности двух ненулевых векторов  =(x₁,y₁,z₁) и  =(x₂,y₂,z₂) имеет вид

   x₁x₂+y₁y₂+z₁z₂=0 (5.4)

5.2. Векторное произведение векторов

Т ройка векторов a,b,c с общим началом в точке О называется правой, если кратчайший поворот оси вектораa к векторуb можно видеть с конца вектораc осуществляющимся против часовой стрелки. В противном случае тройка векторов называется левой.

c c

b

a

Рис.5.1 a b

a,b,c - правая тройка векторов a,b,c - левая тройка векторов

В екторным произведением векторов a иb называется вектор c, обозначаемыйc =a b илиc = a,b , который удовлетворяет трем условиям:

1. c = a   b  sin (a ^b )

2.c a, c b

3 .A,b,c - правая тройка векторов

Из определения векторного произведения следует, что

1.a a = 0

2 .a b = -b a

Если известны координаты векторов a=(x₁,y₁,z₁) и b=(x₂,y₂,z₂), то координаты вектораc =a b вычисляются по формуле:

c =a b = (5.5)

Геометрический смысл векторного произведения:

д лина вектора c =a b равна площади параллелограмма, построенного на векторах a иb:

S =c =a b  = a   b  sin (a ^b )

Или

c

S

b S =

a

Рис.5.2

5.3. Смешанное произведение векторов

С мешанным произведением трех векторов a,b,c называется число, которое получается, если векторыa иb умножить векторно, а затем результат умножить на векторc скалярно. Обозначается смешанное произведение 

a b c. Итак, по определению:

a b c = a,b  c

Если известны координаты векторов a=(x₁,y₁,z₁), b=(x₂,y₂,z₂) и c =(x₃,y₃,z₃), то

a b c = (5.6)

Условие компланарности трех векторов a,b,c имеет вид:

a,b,c – компланарны  a b c = 0  = 0

Г еометрический смысл смешанного произведения: смешанное произведение трех векторов a,b,c равно объему V параллелепипеда, построенного на этих векторах, если a,b,c - правая тройка. Если a,b,c - левая, то смешанное произведение a b c - отрицательно и равно объему с противоположным знаком:

a b c =

Пример 1. Даны векторы a = 4i + 4k, b = -i + 3j + 2k, c = 3i + 5j.

а) вычислить смешанное произведение векторов a,b, 5c;

б) найти модуль векторного произведения 3c иb;

в) вычислить скалярное произведение векторовa и 3b;

г) проверить, будут ли коллинеарны или ортогональны векторыa иb;

д) проверить, будут ли компланарны векторыa,b,c.

►

а) Векторыa,b,c имеют координаты:

a = (4,0,4), b = (-1,3,2), c = (3,5,0) в базисеi,j,k.

По формуле (5.6):

a b  5c = 5 = 5  (-20 - 35 - 40) = -480

б) По формуле (5.5):

c b = = (10, -6, 4)

3c b= 3 = 3  2 = 6

в) По формуле (5.2):

a  3b = 3 a b = 3 (4(-1) + 0  3 + 4  2) = 3  4 = 12

г) Проверим, выполняется ли какое-либо из условий:

a b  x₁ x₂ + y₁ y₂ + z₁z₂ = 0

или a b  = =

Используя координаты данных векторов a = (4,0,4) иb = (-1,3,2), убеждаемся, что ни одно из условий не выполняется:

4  (-1) + 0  3 + 4  2  0  a,b - не ортогональны;

   a,b - не коллинеарны.

д) По формуле (5.3):

a b c = = -20 - 36 - 40 = -96  0  a,b,c - не компланарны.◄

Пример 2. Вершины пирамиды находятся в точках А(2,3,4), В(4,7,3), С(1,2,2), Д(-2,0,-1). Вычислить:

а) площадь грани АВС,

б) объем пирамиды АВСД.

► а) S_АВС = S , , построенного на векторах и . Найдем координаты векторов и :

= (4-2, 7-3, 3-4) = (2,4,-1); = (1-2, 2-3, 2-4) = (-1,-1,-2).

Вычислим векторное произведение  по формуле (5.5):

 = =(-9,5,2).

Используем геометрический смысл векторного произведения :

S = = , откуда получим S_АВС = S = .

б) найдем координаты вектора : = (-4,-3,-5) и смешанное произведение векторов , , по формуле (5.3):

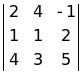  = = = 11.

Объем пирамиды АВСД составляет часть объема параллелепипеда, построенного на векторах , , поэтому, используя геометрический смысл векторного произведения (5.3.4), получим:

V_АВСД = V_{параллелепипеда} = 11 = ◄