5. Исследование линейной корреляционной зависимости между случайными величинами по выборочным данным

Известно, что между случайными величинами и может существовать связь, отличная от функциональной – статистическая. Она появляется обычно тогда, когда имеются общие случайные факторы, влияющие как на одну, так и на другую величину. В частности, корреляционная связь между случайными величинами выражается в том, что на изменение одной случайной величины другая реагирует изменением своего математического ожидания. Функциональная зависимость математического ожидания от значения величины называется регрессией на , а уравнение – уравнением регрессии. Если – линейная функция, имеет место случай линейной корреляционной связи, часто встречающийся в инженерной практике.

Для изучения корреляционной связи между и производят наблюдений, причем измеряют каждую пару значений . По данным полученной выборки исследуют, как при изменении меняется среднее значение . Если зависимость (эмпирическая регрессия) близка к линейной, то выводится формула , наилучшим образом в смысле метода наименьших квадратов, описывающая эмпирическую регрессию . Уравнение называют выборочной прямой линией регрессии на . Это уравнение и служит инструментом для суждения о поведении математического ожидания в зависимости от .

Если нужно получить значение числового критерия , оценивающего степень близости корреляционной линейной зависимости к функциональной, то точечной оценкой коэффициента корреляции по выборочным данным является выборочный коэффициент корреляции .

Исследование линейной корреляционной связи между и с необходимыми пояснениями проведем на примере задачи 14.

Типовые задачи

Задача 14

Рассмотрим зависимость между прочностью (кг/мм²) и выносливостью стали (кг/мм²) по данным 55 наблюдений (табл. 6).

Таблица 6

	50-80	80-110	110-140	140-170	170-200	200-230
25-35	5						5
35-45	4	12					16
45-55		8	5	4			17
55-65		1	5	7	2		15
65-75					1	1	2
	9	21	10	11	3	1	=55

Здесь, например, число 8 означает, что для , лежащих в интервале 80-100 ( – середина этого интервала) раз были получены значения в интервале 45-55. В последней строке табл. 6 приведены суммы (при неизменном значении ), а в последнем столбце – суммы (при неизменном значении ). Очевидно, что .

Корреляционная табл. 6 наглядно показывает выборочное распределение значений для каждого интервала значений , и наоборот. Например, для распределение имеет вид:

Интервал	25-35	35-45	45-55	55-65	65-75
Частота	5	4	0	0	0

а для распределение уже иное:

Интервал	25-35	35-45	45-55	55-65	65-75
Частота	0	12	8	1	0

Выборочное распределение можно изобразить графически в виде поля корреляции (рис. 9); из рисунка видно, что с возрастанием величина имеет тенденцию к возрастанию.

Рис. 9. Графическое изображение распределения

в виде поля корреляции

Характер возрастания оценим, вычислив условное выборочное среднее значение для каждого значения (по серединам интервалов):

– среднее значение при .

Для имеем ,

для будет и т.д.

Аналогичные выкладки одновременно произведем и для . Вычисление оформим в виде вспомогательной табл. 7. Для упрощения расчетов, как и прежде, воспользуемся следующими условными величинами:

и , приняв , , , .

Тогда , .

Порядок заполнения табл. 7: число получено умножением на ; число получено умножением на и на и т.д. Число получено умножением на и на ; далее

и т.д.

Строки и дают условные средние значения величины в зависимости от , столбцы и – условные средние значения в зависимости от .

Таблица 7					65,0	87,5	117,8	145,1	200,0
					-2,00	-1,25	-0,24	0,67	2,50
					-10	-20	-4	10	5
					5	16	17	15	2
									1	1	2	2,00	70,0
								2	1	3	4	1,33	63,3
							4	7		11	7	0,64	56,4
							5	5		10	5	0,50	55,0
						12	8	1		21	-11	-0,52	44,8
					5	4				9	-14	-1,56	34,4

Графики функций и называют эмпирическими линиями регрессии на и на (линии 1 и 2 рис. 10). Эмпирические линии регрессии показывают, как (по данным выборки) изменяется среднее значение одной величины в зависимости от значения, которое приняла другая.

Рис. 10. Эмпирические линии регрессии

Из рис. 10 видно, что по данным выборки (табл. 6) зависимость между и близка к линейной (эмпирические линии регрессии – почти прямые). Сделав такое предположение, найдем уравнение выборочной регрессии на : , где неизвестные параметры и надо определить так, чтобы сумма имела наименьшее значение. Геометрически это сводится к минимизации суммы квадратов отклонений по вертикали точек корреляционного графика (см. рис. 9) прямой . Приравняв к нулю частные производные и , после упрощения получим два условия для определения и (лекции или [1]):

откуда

; ;

;

.

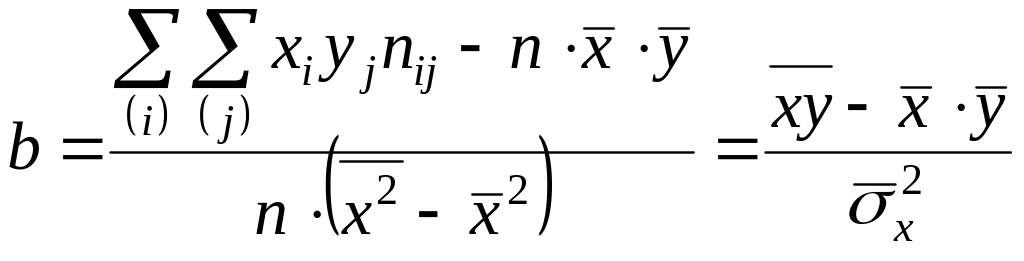Таким образом,

.

Из этого уравнения видно, что выборочная прямая регрессии проходит через среднюю точку корреляционного графика и имеет угловой коэффициент ( называют также выборочным коэффициентом регрессии на ).

Аналогичным образом можно найти уравнение выборочной прямой регрессии на :

выборочный коэффициент регрессии на – .

Для упрощения вычислений снова введем условные переменные

,

и построим условные прямые линии

, .

Результаты вычислений приведены в табл. 8 и 9.

Таблица 8

-2 -1 0 1 2 3	9 21 10 11 3 1	-18 -21 0 11 6 3	4 1 0 1 4 9	36 21 0 11 12 9	-14 -11 5 7 4 2	28 11 0 7 8 9
	55	-19	-	89	-	60

Таблица 9

-2 -1 0 1 2	5 16 17 15 2	-10 -16 0 15 4	4 1 0 1 4	20 16 0 15 8	-10 -20 -4 10 5	20 20 0 10 10
	55	-7	-	59	-	60

Здесь для контроля вычислений сумма сосчитана дважды.

Найдем необходимые величины:

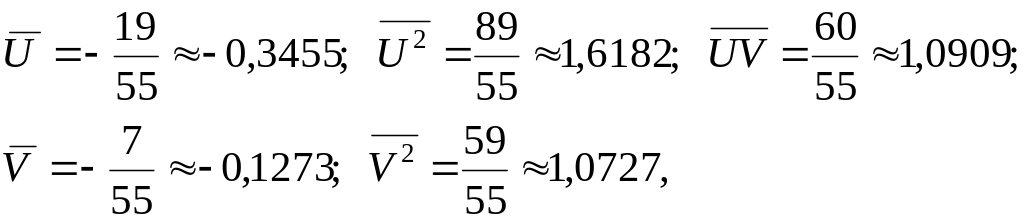
тогда

; .

Вспомогательные линии регрессии имеют вид:

или, что то же самое,

Сделав подстановку

и ,

найдем выборочные прямые регрессии на и на :

С учетом погрешностей вычислений и округлений эти прямые проходят через точку с координатами ; и являющуюся центром распределения данной выборки.

Здесь , – угловые коэффициенты выборочных прямых регрессии.

На рис. 11 изображены выборочная (1) и эмпирическая (2) линии регрессии на . Аналогично можно изобразить линии регрессии на .

“Тесноту” линейной корреляционной зависимости от измеряют отношением меры разброса ординат выборочной прямой относительно к мере общего разброса значений , т.е. числом , где , , так что . Это число называют выборочным коэффициентом корреляции и вычисляют по формуле . Произведение коэффициентов регрессии равно квадрату коэффициента корреляции: .

Рис. 11. Выборочная (1) и эмпирическая (2) линии регрессии на

При функциональной связи между и в выборке прямые регрессии совпадают: и . При линейная связь и отсутствует, хотя нелинейная корреляционная связь может и существовать. Близость к единице говорит о наличии корреляционной связи, достаточно близкой к линейной.

При построении выборочных прямых регрессии , , поэтому и .

Для оценки действительного значения коэффициента корреляции между и по выборочному коэффициенту при можно построить доверительный интервал , отвечающий надежности . Из условия найдем , используя таблицу нормального распределения (прил. 1):

, где .

В разбираемом примере . Пусть . По таблице прил. 1 найдем , отсюда . Поэтому с вероятностью получается в генеральной совокупности, из которой взята рассматриваемая выборка, значение коэффициента корреляции в пределах 0,81-0,841.

При доверительной вероятности 0,997 и можно считать, что действительное значение коэффициента корреляции лежит в пределах

( ) – правило “трех сигм”.

Если по данным выборки окажется мал (близок к нулю), у нас не будет по данному материалу оснований считать, что и связаны линейной корреляционной связью. В этом случае при выполнении условия считаем, что лишь случайно и связь наблюдениями не доказывается. При считают линейную корреляционную связь и реальной. В нашем примере .

Таким образом, данные выборки говорят о достаточно тесной линейной корреляционной связи между прочностью и выносливостью стали. Выборочные прямые регрессии могут служить достаточно надежно для суждения о том, какое значение примет одна величина при фиксированном значении другой.