Условие задачи:

Q=60-P

TC₁=3q₁²+2

TC₂=15q₂+18

Модель	q1	q2	Доля1	Доля2	Q	P	π1	Доляπ 1	π2	Доляπ 2	π
Курно	5	20	20	80	25	35	98	20,4	382	79,6	480
Штакельберг	4,8	21,4	18,3	81,7	26,2	33,8	91,12	19,2	384,32	80,8	475,44
Картельное соглашение	2,5	20	11,1	88,9	22,5	37,5	71	14	432	86	503
1 фирма нарушает картел. соглашение	5	20	20	80	25	35	98	20,4	382	79,6	480
2 фирма нарушает картел. соглашение	2,5	21,25	10,5	89,5	23,75	36,25	69,9	13,9	433,6	86,1	503,5

Решение задачи: а) м. Курно.

Фирмы не взаимодействуют друг с другом.

Найдем прибыль обеих фирм:

Общие издержки фирм (TС) даны в условии задачи, найдем выручку (TR):

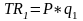
Таким образом, формула прибыли примет вид:

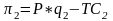
Определим, чему равна цена (Р), выведем её из формулы объема продаж рынка (дана в условии задачи):

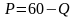
С учетом того, что на рынке присутствуют две фирмы, объем рынка будет иметь вид:

Таим образом, формула цены будет иметь вид:

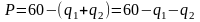
Учитывая, что цена товара для обеих фирм будет одинакова, подставляем цену (Р) и функции издержек (ТС) в формулу прибыли:

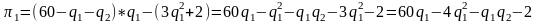
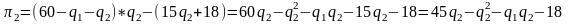
Обе фирмы максимизируют прибыль. Условие максимизации:

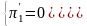
Найдем производные прибыли обеих фирм:

Решим систему способом вычитания, для этого умножим первое уравнение на 2:

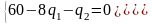получим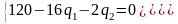

Вычтем из первого уравнения второе

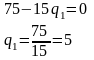
По мере нахождения параметров заносим их значения в таблицу.

Выразим из первого уравнения системы

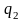
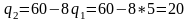
Далее находим все необходимые значения:

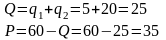
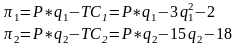
Найдем доли рынка каждой фирмы:

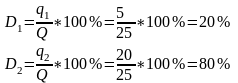
Найдем доли прибыли каждой фирмы в общей прибыли:

Б) м. Штакельберга

В модели Штакельбергаолигополисты выбирают две линии поведения: лидера и последователя. Последователь будет реагировать на действия лидера, приспосабливая свой выпуск в соответствии с выпуском лидера. В свою очередь последователь предполагает, что на его действия не реагируют.

Объем производства фирмы-лидера будет зависеть только от ее объема производства.

Определим, кто из фирм будет лидером, а кто последователем. Для этого найдем и сравним функции предельных издержек двух фирм.

MC₁=TC₁`

MC₂=TC₂`

MC₁=6q₁

MC₂=15

Лидером будет являться та фирма, у которой предельные издержки будут меньше. В нашем случае это 2 фирма, соответственно, 1 фирма – последователь.

Определив линии поведения, начинаем решать модели с ПОСЛЕДОВАТЕЛЯ!

1 ФИРМА ПОСЛЕДОВАТЕЛЬ

Найдем прибыль фирмы:

Общие издержки фирмы (TС) даны в условии задачи, найдем выручку (TR):

Таким образом, формула прибыли примет вид:

Определим, чему равна цена (Р), выведем её из формулы объема продаж рынка (дана в условии задачи):

С учетом того, что на рынке присутствуют две фирмы, объем рынка будет иметь вид:

Таим образом, формула цены будет иметь вид:

Учитывая, что цена товара для обеих фирм будет одинакова, подставляем цену (Р) и функции издержек (ТС) в формулу прибыли:

Первая фирма максимизирует свою прибыль. Условие максимизации:

Найдем производную прибыли фирмы:

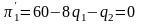
Выведем из уравнения объем производной первой фирмы, который будет зависеть от объема производства второй фирмы:

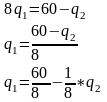
2 ФИРМА ЛИДЕР

Найдем прибыль 2 фирмы

Общие издержки фирмы (TС) даны в условии задачи, найдем выручку (TR):

Таким образом, формула прибыли примет вид:

Определим, чему равна цена (Р), выведем её из формулы объема продаж рынка (дана в условии задачи):

С учетом того, что на рынке присутствуют две фирмы, объем рынка будет иметь вид:

Таим образом, формула цены будет иметь вид:

Учитывая, что цена товара для обеих фирм будет одинакова, подставляем цену (Р) и функции издержек (ТС) в формулу прибыли:

Таким образом, согласно формуле прибыль фирмы-лидера (2) будет зависеть не только от ее объема производства (q₂), но и от объема производства первой фирмы (q₁), что противоречит модели Штакельберга. Для того, чтобы избавится от этого противоречия подставим в формулу прибыли:

Приведем подобные к общему знаменателю:

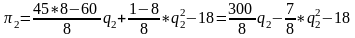
Фирма максимизируют прибыль. Условие максимизации:

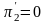
Найдем производную прибыли 2 фирмы:

Подставим в уравнение значение q₂

Далее находим все необходимые значения:

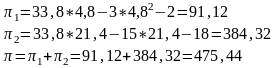
Найдем доли рынка каждой фирмы:

Найдем доли прибыли каждой фирмы в общей прибыли: