
- •Тема Основы финансовых вычислений
- •Таким образом, можно сформулировать ряд выводов:
- •Временная ценность денег — одно из фундаментальных понятий финансов.
- •Процесс накопления (наращивания)капитала прослеживается следующим образом:
- •Тема Финансовый анализ
- •Основные показатели финансового анализа деятельности предприятия
- •Типы финансирования деятельности организации
- •Тема Структура активов и капитала. Финансовая устойчивость
- •Тема Ликвидность и платежеспособность
- •Расчет интегральной оценки финансовой устойчивости
- •Тема Прибыльность и рентабельность
- •Тема Операционная активность
- •Тема Деловая активность
- •Тема Факторный анализ использования активов и капитала
- •Тема Анализ рентабельности собственного капитала
- •Тема Анализ эффективности денежного потока
- •Интегральная оценка финансового состояния
Практические занятия «Финансовый менеджмент»
Управление финансами является составной частью общей системы управления социально-экономическими процессами. Оно направлено на совершенствование системы отношений, призванных нормализовать финансовые ресурсы, необходимые для социально-экономического развития общества.
Цель управления финансами – финансовая устойчивость и финансовая независимость, проявляющиеся в макроэкономической сбалансированности, профиците бюджета, снижении государственного долга, твердости национальной валюты, в сочетании экономических интересов государства, бизнеса и общества в целом.
Управление финансами осуществляется на всех уровнях финансовой системы. Оно бывает общегосударственным, которое устанавливает общие принципы, правила и нормы, а также обеспечивает проведение единой финансово-бюджетной политики, налоговой, валютной и денежно-кредитной политики в Российской Федерации; и управление финансами отдельных субъектов управления.
Методами и формами управления финансами служат финансовое планирование, прогнозирование, финансовое регулирование, финансовый контроль, оперативное управление, система методов мобилизации финансовых ресурсов и др. В новых условиях хозяйствования и становлении рыночных отношений в России особое значение имеет финансовый менеджмент, призванный обеспечить эффективное управление ресурсами предприятий различных форм собственности.
Финансовая система – это совокупность различных сфер финансовых отношений (звенья финансовой системы), в процессе которых образуются и используются фонды денежных средств. Это совокупность централизованных и децентрализованных денежных фондов.
Заполнить в таблице содержание и сущность основных концепции и привести пример (указать основоположников)
Название концепции |
Сущность и содержание |
Основоположники указанной концепции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема Основы финансовых вычислений
Цена капитала на финансовом рынке определяется процентной ставкой. Она зависит от ряда факторов, основными из которых являются спрос и предложение денежных ресурсов на финансовом рынке.
Процентная ставка используется для определения стоимости денег с учетом временного фактора. Могут применяться простые, сложные и непрерывно начисляемые процентные ставки.
Таким образом, можно сформулировать ряд выводов:
стоимость — это расчетный показатель; цена — декларированный, т. е. объявленный, который можно видеть в прейскурантах, ценниках, котировках; цена открыта, общеизвестна, тогда как стоимость в известном смысле конфиденциальна;
в любой момент времени на данном рынке цена однозначна, тогда как стоимость многозначна, при этом число оценок стоимости зависит от числа профессиональных участников рынка;
с известной долей условности можно утверждать, что стоимость первична, а цена вторична, поскольку в условиях равновесного рынка цена, во-первых, количественно выражает внутренне присущую активу стоимость; во-вторых, стихийно устанавливается как среднее из оценок стоимости, рассчитываемых участниками рынка.
Основные теоретические положения концепции временной ценности денег (Time Value of Money, TVM) были сформулированы в 1930 г. Ирвином Фишером в работе "Теория процента: как определить реальный доход в процессе инвестиционных решений".
Сущность временной ценности денег состоит в том, что одна и та же сумма денег в разное время имеет различную ценность; эта ценность в настоящее время всегда выше, чем в любом будущем периоде
С экономической точки зрения процент представляет собой плату за использование денежных средств одного лица (кредитора) другим лицом (заемщиком, дебитором), выраженную в сотых долях от исходной суммы.
Процентная ставка (англ. interest rate) — сумма, указанная в процентном выражении к сумме кредита, которую платит получатель кредита за пользование им в расчёте на определённый период (месяц, квартал, год). С позиции теории денег, процентная ставка — это цена денег как средства сбережения.
Денежный поток, кэш-фло, кэш-флоу (от англ. Cash Flow) или поток наличных денег — одно из важнейших понятий современного финансового анализа, финансового планирования и управления финансами.
Временная ценность денег — одно из фундаментальных понятий финансов.
Шесть (финансовых) функций сложного процента позволяют устанавливать количественную взаимосвязь стоимости денег в разные периоды времени и получать количественную оценку временной стоимости денег как капитала, способного приносить доход.
Процесс накопления (наращивания)капитала прослеживается следующим образом:
Год |
Накопленная сумма при начислении простого процента, тыс. ден. ед. |
Накопленная сумма при начислении сложного процента, тыс. ден. ед. |
|
FV=PV (l + i*n)
|
FV=PV (l + i)n |
1-й |
400 + 400 х 0,10 = 440 |
400 + 400x0,10 = 440 |
2-й |
440 + 400x0,10 = 480 |
440 + 440x0,10 = 484 |
3-й |
480 + 400x0,10 = 520 |
484 + 484x0,10 = 532,4 |
Временная оценка денежных потоков основана на использовании шести функций сложного процента существует в следующей последовательности:
Базовые финансовые функции сложного процента
Номер функции сложного процента |
Прямая функция, коэффициент |
Характеристика функции |
1.Будущая стоимость денежной единицы (накопленная сумма единицы) |
FV=PV (l + i)n
|
(1+r)n — множители наращения |
Будущая стоимость денежной единицы при более частом, чем 1 раз в год, начислении процентов |
|
|
2. Будущая стоимость обычного аннуитета (PMT - регулярный платеж в начале каждого периода) |
|
|
3 Фактор фонда возмещения капитала - периодический взнос в фонд накопления
|
|
|
4.Дисконтирование - текущая стоимость денежной единицы при начислении процентов 1 раз в год
|
|
|
5.Текущая стоимость обычного аннуитета при платежах в конце каждого периода
|
|
|
6. Взнос на амортизацию единицы |
|
|
Обозначения в приведенных выше формулах:
PV — текущая стоимость денежной единицы;
i — годовая процентная ставка;
n — количество лет (периодов);
k — количество платежей в течение одного года (периода);
FV – будущая стоимость денежной единицы;
РМТ – единовременный платеж n-ого периода.
Рассчитайте по условиям задач значения базовых функций сложного процента.
Функция сложного процента
|
Значение коэффициентов |
Итоговое значение |
Инвестору за 5 лет необходимо накопить капитал для реализации инвестиционного проекта в сумме 2,5 млн. рублей, определить периодически депонируемый поток платежей (ежемесячно) от дохода, по ставке 14% годовых.
|
|
|
Рассчитать будущую стоимость потока арендных платежей, возникающих в конце года, если годовой арендный платеж первые четыре года составляет 400 тыс. руб., затем он уменьшится на 150 тыс. руб. и сохранится в течение трех лет. Ставка дисконта — 12%.
|
|
|
Сбербанк выдал кредит на сумму 2 млн руб. сроком на 10 лет под 12% годовых. Погашение кредита должно производиться равными ежемесячными выплатами в конце каждого года, включающими погашение основного долга и процентные платежи. |
|
|
Достаточно ли положить на счет 600 тыс. рублей на депозитный счет с ежемесячным начислением сложных процентов по ставке 10% годовых для приобретения через 5 лет дома стоимостью 900 тыс. руб. |
|
|
Определите современную (текущую) величину вложенных средств, которые должны быть выплачены через 4 года в сумме 300 тыс. рублей. В течение этого периода на первоначальную сумму начисляются сложные проценты по ставке 14 % годовых?
|
|
|
Какую сумму необходимо вложить родителям в банк, начисляющий 14 % годовых, чтобы хватило перечислять за обучение по 60 тыс. рублей в год (период обучения 4 года). |
|
|
Дополнительные вопросы
Как изменится значение приведенной стоимости 1 тыс. руб., получаемых через год, если ставка дисконтирования уменьшится?
Как изменится значение будущей стоимости 1 тыс. руб., если процентная ставка возрастет с10до11%в год?
Существует ли связь между приведенной величиной будущих денежных потоков, полученных за счет инвестированного капитала, и ставкой доходности инвестиций? Объясните ответ.
Предположим, что сегодня вы вложили на накопительный счет 50 тыс. руб. сроком на 5 лет под 10% в год, а в последующие 4 года вы ежегодно вкладывали 10 тыс. руб. под 8% в год. Определите сумму денег, которую вы будете иметь на своем накопительном счете через 5 лет, если проценты на ваши вклады начислялись в конце каждого года.
Вы занимаете сумму денег Р и обязуетесь через год (или менее одного года)выплатить большую сумму F в виде разового платежа. В этом случае процентная ставка определяется на основе формулы:
F=P(1 + r).
Откуда значение r будет равно:
r=F/P-1
Пример Петров взял ссуду 100 тыс. руб. с условием возврата через год ссуды и процентов по ней в виде разового платежа 112 тыс. руб. Определить процентную ставку по займу.
r = 112 000/100 000 - 1 = 0,12, или 12% в год.
Если заем выдается на срок более 1 года (п лет), то процентная ставка определяется из выражения:
r =(F/P)1/n -1;
Пример . Семенов получил в Сбербанке банке ссуду 120 тыс. руб. с условием возврата через 4 года 180 тыс. руб. Определить процентную ставку по ссуде.
Примем F= 180 000 руб., Р - 120 000 руб. и п = 4 года. Подставим эти значения в формулу:
r = (180 000/120 ООО)1/4 - 1 = 0,107, или 10,7% в год.

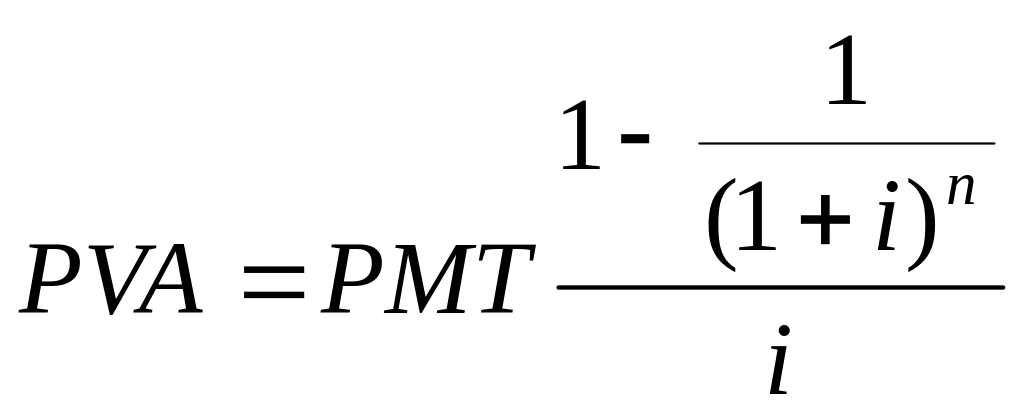
 коэффициент
приведения ренты
коэффициент
приведения ренты