
- •Федеральное агентство по образованию
- •Содержание
- •Введение
- •1. Цели и задачи дисциплины
- •2. Требования к уровню освоения содержания дисциплины
- •2.1. Инновационные технологии, используемые в учебном процессе
- •3. Объем дисциплины
- •Экономика и управление на предприятии (по отраслям)
- •3.2. Распределение часов по темам и видам учебной работы
- •4. Содержание курса Раздел 1. Дифференциальное исчисление Тема 1. Предел и непрерывность функции
- •Тема 2. Дифференциальное исчисление функций одной переменной
- •Тема 3. Дифференциальное исчисление функций нескольких переменных
- •Раздел 2. Интегральное исчисление дифференциальные уравнения. Ряды Тема 4. Интегралы
- •Тема 5. Дифференциальные уравнения
- •Тема 6. Ряды
- •Раздел 3. Линейная алгебра с элементами аналитической геометрии Тема 7. Векторная алгебра
- •Тема 8. Элементы аналитической геометрии
- •Тема 13. Случайные величины и их числовые характеристики
- •Раздел 6. Марковские цепи в экономике
- •Тема 2. Дифференциальное исчисление функций одной переменной
- •Тема 3. Дифференциальное исчисление функций нескольких переменных
- •Раздел II. Интегральное исчисление. Дифференциальные уравнения. Ряды
- •Тема 4. Интегралы
- •Тема 5. Дифференциальные уравнения
- •Раздел 3. Линейная алгебра с элементами аналитической геометрии
- •Тема 7. Векторная алгебра
- •Тема 8. Элементы аналитической геометрии
- •Тема 9. Матрицы и определители
- •Тема 10. Системы линейных уравнений (слу)
- •Раздел 4. Теория вероятностей
- •Тема 12. Основные понятия теории вероятностей. Случайные события
- •Тема 13. Случайные величины и их числовые характеристики
- •Тема 14. Основные распределения случайных величин
- •Тема 15. Функция случайной величины
- •Раздел 5. Линейное программирование
- •Тема 18. Задача линейного программирования (лп)
- •П.1.2. Графическое решение задачи лп
- •Тема 19. Симплексный метод линейного программирования Это практическое занятие можно провести в форме деловой игры и дискуссии.
- •Решите следующие задачи симплекс-методом:
- •Тема 3. Двойственность в линейном программировании
- •Тема 20. Транспортная задача Это занятие можно провести в форме деловой игры и дискуссии.
- •П.2.1. Замкнутая модель тз
- •Тема 22. Матричные игры Это занятие можно провести в форме деловой игры и дискуссии. П.3.1. Матричные игры с седловой точкой
- •П.3.3. Решение игры симплекс-методом
- •Раздел 6. Марковские цепи в экономике
- •Тема 23. Потоки событий
- •1.1. Простейший поток событий
- •1.2. Системы массового обслуживания с отказами
- •Тема 24. Уравнения Колмогорова
- •1.3. Системы массового обслуживания с ограниченной очередью.
- •Тема 25. Системы массового обслуживания
- •Раздел 7. Нелинейные задачи и оптимизация на графах
- •Тема 26. Задача динамического программирования
- •Тема 27. Основы теории графов
- •3.1. Основные понятия
- •Тема 28. Задача о коммивояжере
- •Тема 29. Задача об оптимальном потоке
- •Тема 30. Задача о назначениях
- •3.3. Задача о назначении
- •Тема 31. Задача сетевого планирования
- •3.4. Сетевой график
- •Раздел 8. Исследование функций и экономическое моделирование
- •7. Темы контрольных работ и методические указания по их выполнению
- •Вариант 1
- •2. Решите систему линейных уравнений
- •Вариант 2
- •2. Решите систему линейных уравнений
- •Вариант 3
- •2. Решите систему линейных уравнений
- •Вариант 4
- •Вариант 6
- •А) 150 мальчиков; б) от 150 до 200 мальчиков? Вариант 7
- •Вариант 8
- •6. Известно, что вероятность опоздания ежедневного поезда на станцию равна 0,2. Какова вероятность того, что в течение 200 дней поезд опоздает на станцию а) 50 раз; б) от 100 до 150 раз? Вариант 9
- •Методические рекомендации к выполнению контрольной работы
- •Элементы теории вероятности и математической статистики
- •7.2.3. Контрольные задания для студентов заочной формы обучения всех специальностей по прикладной математике (III семестр) представлены в методическом пособии [7]
- •7.2.4. Контрольные задания для студентов заочной формы обучения всех специальностей (направлений) Прикладная математика (IV семестр)
- •Методические указания к выполнению задач (к/р IV семестр)
- •Тема 1. Модели оптимального планирования
- •Тема 2. Системы и модели массового обслуживания
- •Модели смо с ожиданием для решения задач № 26-30
- •Тема 3. Игровые методы и модели в торговле
- •3. Критерий пессимизма – оптимизма Гурвица.
- •Тема 4. Методы и модели сетевого планирования и управления
- •8. Вопросы для подготовки к экзамену 1-ый семестр
- •3 Семестр
- •4 Семестр
- •9. Учебно-методическое обеспечение дисциплины
- •9.1. Литература основная
- •Дополнительная Разделы 1, 2 и 3
- •Раздел 4
- •9.2 Методическое обеспечение
- •9.3 Материально-техническое и информационное обеспечение дисциплины
- •Математика
Методические рекомендации к выполнению контрольной работы
Векторная алгебра и элементы аналитической геометрии
Для решения задачи 1 и задачи 2 необходимо изучить следующую литературу:
Глава 3, стр. 63-74,
Глава 4, стр. 95-101
Глава 9, § 1-13, стр. 222-251
Теперь рассмотрим применение изученных формул на примерах.
ЗАДАЧА 1
В декартовой прямоугольной системе координат даны вершины пирамиды А1 В1 С1 D1. Найдите:
а) длину ребра А1 В1;
б)
косинус угла между векторами![]() ;
;
в) уравнение ребра А1 В1;
г) уравнение грани А1 В1 С1;
д) уравнение высоты, опущенной из вершины D1 на грань А1 В1 С1;
е)
координаты векторов
![]() ,
,![]() ,
,![]() ,
и докажите, что они образуют линейно
независимую систему;
,
и докажите, что они образуют линейно
независимую систему;
ж)
координаты вектора
![]() ,
где
,
где![]() –
середины ребер А1
D1 и
В1
С1
соответственно;
–
середины ребер А1
D1 и
В1
С1
соответственно;
з)
разложение вектора
![]() по базису
по базису![]() если А1(-2,2,2),
В1(1,-3,0),
С1(6,2,4),
D1(5,7,-1).
если А1(-2,2,2),
В1(1,-3,0),
С1(6,2,4),
D1(5,7,-1).
Решение
а)
Найдем координаты вектора
![]() по
формуле
по
формуле
![]() =
=
![]() XВ
XВ![]() -
XА
-
XА![]() ;
YВ
;
YВ![]() -
YА
-
YА![]() ;
ZВ
;
ZВ![]() -
ZА
-
ZА![]()
![]() ,
где (ХА
,
где (ХА![]() ,
YА
,
YА![]() ,
ZА
,
ZА![]() )
– координаты точки А1,
(ХВ
)
– координаты точки А1,
(ХВ![]() ,
YВ
,
YВ![]() ,
ZВ
,
ZВ![]() )
– координаты точки В1.
)
– координаты точки В1.
Итак,
![]() =
=![]() Тогда
Тогда![]() =
=![]() .
.
Итак,
длина отрезка
![]() (или длина вектора
(или длина вектора![]() )
равна
)
равна![]() .
Это и есть искомая длина ребра.
.
Это и есть искомая длина ребра.
б)
Координаты вектора
![]() =
=![]() уже
известны, осталось определить координаты
вектора
уже
известны, осталось определить координаты
вектора![]() :
:![]() =
=![]() .
.
Угол
между векторами![]() и
и![]() вычислим
по формулеcos
вычислим
по формулеcos![]() =
=![]() ,
,
где
скалярое произведение векторов
![]() и
и![]() равно
(
равно
(![]() ,
,![]() )=
3
8 + (-5)
0 + (-2)
2
= 24 + 0 -
4=20,
)=
3
8 + (-5)
0 + (-2)
2
= 24 + 0 -
4=20,
![]() =
=![]() ,
,![]() =
=![]()
Итак,
cos![]() =
=![]() =
=![]() .
.
в)
Координаты точки А1(-2,2,2)
обозначим соответственно Х0
= -2,
У0
= 2, Z0=2,
а координаты точки В1
(1,-3,0)
через Х1=1,
У1
= -3,
Z1=0
и воспользуемся уравнением прямой в
пространстве, проходящей через две
точки:
![]() .
.
Следовательно,
уравнение ребра А1В1
имеет вид
![]() или
или![]()
г)
Обозначим координаты векторов
![]() и
и![]() через
Х1=3,
У1=
-5,
через
Х1=3,
У1=
-5,
![]() 1=
-2
и Х2=8,
У2=
0,
1=
-2
и Х2=8,
У2=
0,
![]() 2=2
соответственно. Векторное произведение
данных векторов определяется формулой
2=2
соответственно. Векторное произведение
данных векторов определяется формулой
![]()
Так
как данный вектор перпендикулярен грани
А1
В1
С1
то можно воспользоваться уравнением
плоскости, проходящей через точку (Х0,
У0,
![]() 0)
перпендикулярно вектору
0)
перпендикулярно вектору
![]() ,
которое имеет вид
,
которое имеет вид
А
![]() .
.
Подставим
координаты точки А1
(Х0=-2,
У0=2,
![]() 0=2)
и координаты перпендикулярного вектора
А=-10,
В=-22,
С=40 в это уравнение:
0=2)
и координаты перпендикулярного вектора
А=-10,
В=-22,
С=40 в это уравнение:
– 10
( Х + 2 ) -
22 (У -
2) + 40 (![]() -
2) = 0. Раскроем скобки и приведем подобные
члены – 10 х – 22 у + 40z + (-
20 + 44-80)=0.
Итак, уравнение грани А1
В1
С1
имеет вид: -10х
-
22у + 40 z-56=0
или
-
2) = 0. Раскроем скобки и приведем подобные
члены – 10 х – 22 у + 40z + (-
20 + 44-80)=0.
Итак, уравнение грани А1
В1
С1
имеет вид: -10х
-
22у + 40 z-56=0
или
-5х - 11у + 20 z - 28=0.
д)
Вектор
![]() является
направляющим вектором высоты, опущенной
из вершиныD1
на грань
А1В1С1.
Воспользуемся уравнением прямой в
пространстве, проходящей через точку
является
направляющим вектором высоты, опущенной
из вершиныD1
на грань
А1В1С1.
Воспользуемся уравнением прямой в
пространстве, проходящей через точку
 с заданным направляющим вектором:
с заданным направляющим вектором: ,
где
,
где![]() –
координаты
точки D1.
Отсюда искомое уравнение:
–
координаты
точки D1.
Отсюда искомое уравнение:
![]() или
или![]()
е)
Координаты вектора
![]() =
=![]() =
=![]() .
.
Обозначим
![]()
![]() =
=![]() ,
,![]()
![]() =
=![]() ,
,![]() .
.
Чтобы
доказать, что векторы
![]() образуют линейно независимую систему
векторов необходимо убедиться, что
определитель третьего порядка,
составленный из координат этих векторов,
образуют линейно независимую систему
векторов необходимо убедиться, что
определитель третьего порядка,
составленный из координат этих векторов,
 отличен
от 0. Определитель третьего порядка
равен
отличен
от 0. Определитель третьего порядка
равен
 =
= -
-
 +
+ =
=
=![]()
Вычислим определитель
 =3
=3![]() –
(–5)
–
(–5)![]() +(–2)
+(–2)![]() = 3
= 3![]() (0
(0![]() (–3)
–
5
(–3)
–
5![]() 2)+5
2)+5![]() (8
(8![]() (–3)
– 7
(–3)
– 7![]() 2)–
2)–
-
2![]() (8
(8![]() 5– 7
5– 7![]() 0)
=3
0)
=3![]() (–10)+5
(–10)+5![]() (–24
– 14)
–
2
(–24
– 14)
–
2![]() 40=–30
– 190
– 80
= –300.
40=–30
– 190
– 80
= –300.
Так
как данный определитель отличен от 0,
то вектора
![]() образуют линейно независимую систему.
образуют линейно независимую систему.
ж) Сначала найдем координаты точек М и N соответственно. Координаты точки
М
=![]() =
=![]() =
=![]()
N
=![]() =
=![]() =
=![]() .
.
Получаем
вектор
![]() =
=![]() .
.
з)
Обозначим через
![]() координаты
вектора
координаты
вектора![]() в
базе
в
базе![]() .
.
Тогда
![]() =
=![]() =
=![]() .
.
Так как
![]() =
=![]() +
+![]() +
+![]() ;
;![]()
=![]() +
+![]() +
+![]() =
=![]() ,
,
то приравнивая соответствующие координаты, получим систему трех линейных уравнений с тремя неизвестными.
(1) 
Решим
данную систему уравнений с помощью
формул Крамера (см.
![]() глава 10, стр. 268). Рассмотрим произвольную
систему трех линейных уравнений с тремя
неизвестными:
глава 10, стр. 268). Рассмотрим произвольную
систему трех линейных уравнений с тремя
неизвестными:
Тогда
![]() =
=![]() z
z![]() ,
где
,
где

Для системы (1) определитель
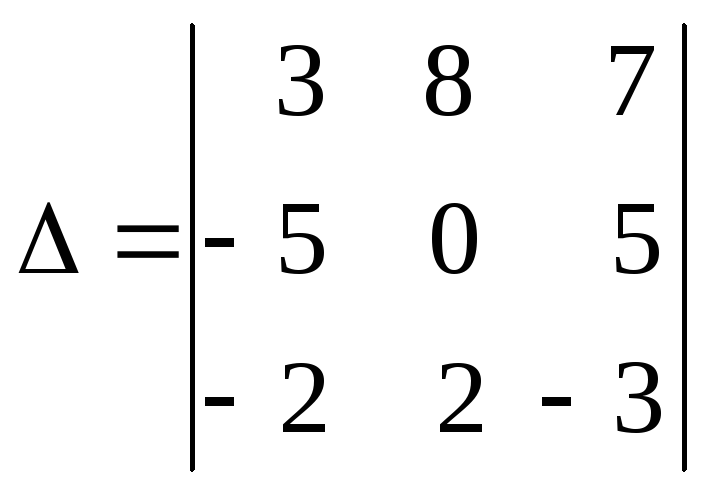 =3
=3 –8
–8 +7
+7 =
=
=
3 ( –10)
–
8![]() (
15 + 10 ) + 7 (–10)
= –30
–
200 –
70 = –300;
(
15 + 10 ) + 7 (–10)
= –30
–
200 –
70 = –300;
 = 2
= 2![]() –8
–8
 +7
+7 =
=
![]()
 =3
=3 –2
–2 +7
+7 =
=
=3![]()
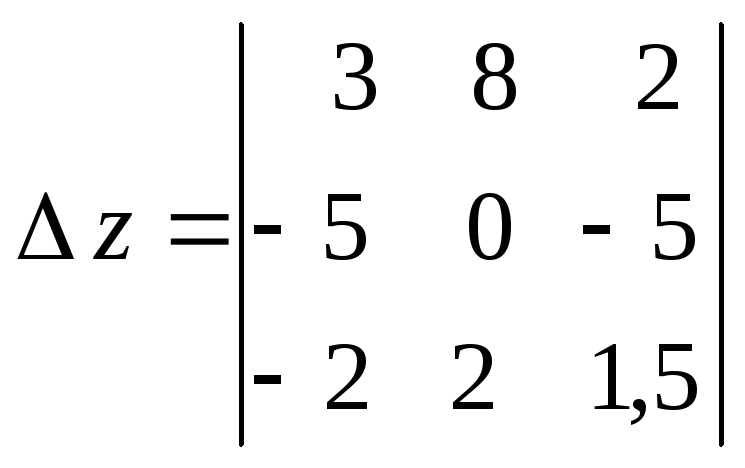 =3
=3 –8
–8 +2
+2 =
=
=![]()
По формулам Крамера
![]()
![]()
Итак,
разложение вектора![]() по базису (
по базису (![]() )
имеет вид
)
имеет вид
![]() =
=
![]()
ЗАДАЧА 2
Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) с помощью обратной матрицы.

Решение
а)
Метод Крамера состоит в решении системы
линейных уравнений по формулам Крамера
![]() ,
,
где
![]() (Подробности
смотрите в пунктез)
задачи 1.
(Подробности
смотрите в пунктез)
задачи 1.
Так
как
![]()
![]()
![]()
![]() ;
то
;
то![]()
б) решим данную систему уравнений методом Гаусса. Метод Гаусса состоит в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида из которой последовательно, начиная с последнего уравнения легко находят все неизвестные системы.
Составим расширенную матрицу данной системы.
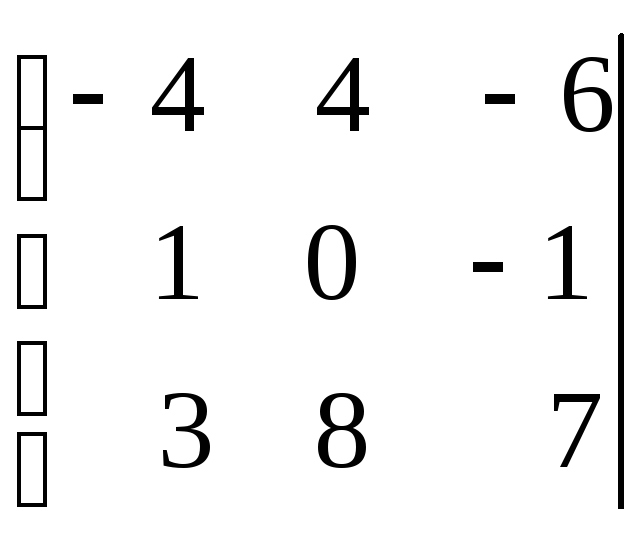
![]()
Поменяем местами первую и вторую строки матрицы чтобы в ее левом верхнем углу была единица. Получим матрицу,

![]()
Умножим каждый элемент первой строки матрицы на 4 и прибавим полученные числа к соответствующим элементам второй строки. Матрица примет вид,

 =
=
![]()
Умножим каждый элемент первой строки матрицы на –3, и прибавим полученные числа к соответствующим элементам третьей строки. Получим:

 =
=
![]() .
.
Разделим каждый элемент второй строки матрицы на 4, чтобы второй элемент, стоящий на главной диагонали матрицы, стал равным 1.

![]() .
.
Умножим каждый элемент второй строки матрицы на –8 и прибавим полученные числа к соответствующим элементам третьей строки:


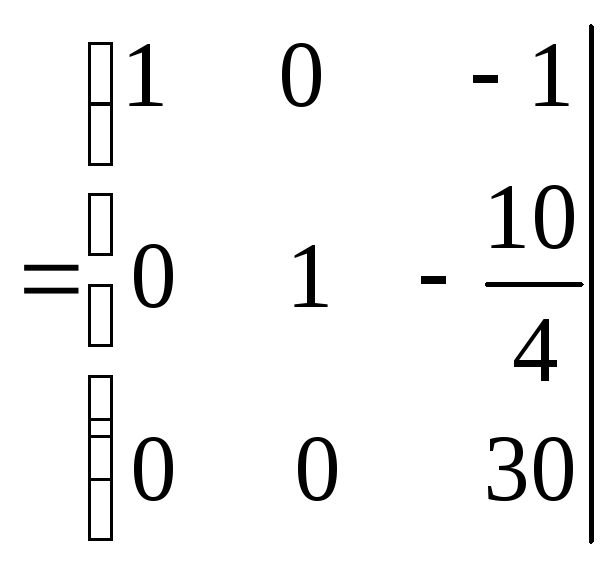
 .
.
Данная
матрица соответствует системе уравнений
 ,
решение которой совпадает с решением
исходной системы. Начиная с последнего
уравнения, несложно найти все неизвестные.
,
решение которой совпадает с решением
исходной системы. Начиная с последнего
уравнения, несложно найти все неизвестные.
Действительно,
так как
![]() и
и![]() ,
то
,
то![]()
Отсюда,
![]() Из
Из![]() имеем
имеем![]()
Ответ:
![]() .
.
в)
Решение системы в этом случае равно
![]() =
=![]()
![]() ,
где
,
где
![]() =
=
 – обратная матрица для матрицы
– обратная матрица для матрицы
![]() =
=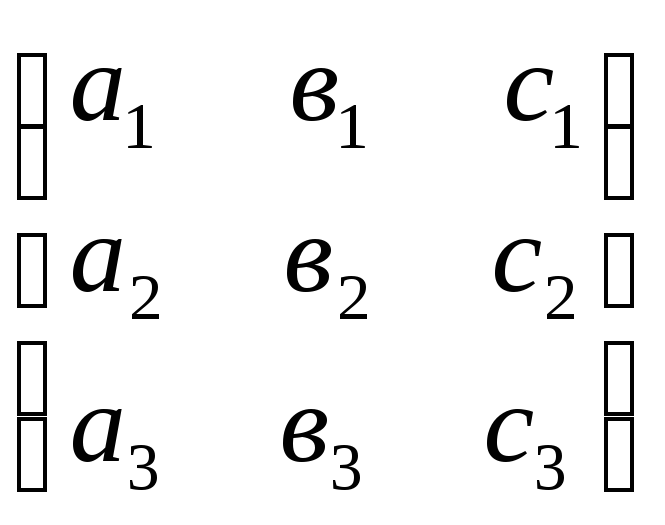 ,
,![]() –столбец
свободных членов,
–столбец
свободных членов,
![]() –
определитель этой матрицы. (Общую запись
системы трех линейных уравнений с тремя
неизвестными смотрите в задаче 1, пункт
з, система 2).
–
определитель этой матрицы. (Общую запись
системы трех линейных уравнений с тремя
неизвестными смотрите в задаче 1, пункт
з, система 2).
Составим матрицу состоящую из коэффициентов при неизвестных данной системы:
А
=
 .
.
Вычислим
ее определитель
 =–4
=–4 –4
–4 –6
–6![]() =
=
=![]() .
.
Вычислим алгебраические дополнения для всех элементов матрицы А:

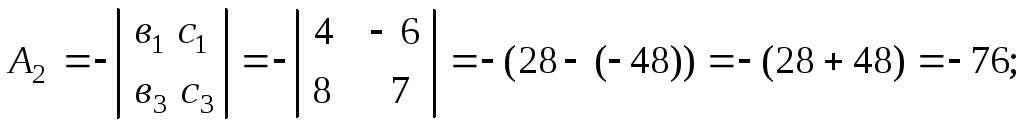



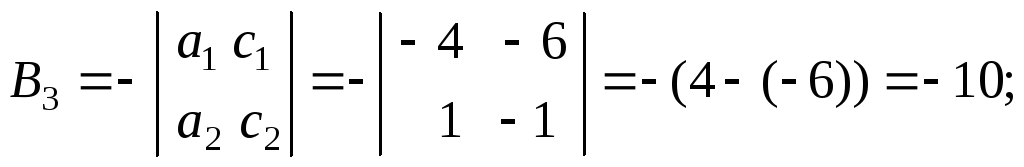



Тогда![]()
![]() =
=
 =
= и
и
![]() =
=
![]()
![]() =
=
= =
= =
=![]() =
=![]() .
.
Отметим, что ответы, полученные при решениями разными методами совпадают между собой.
Ответ:
![]()

