
- •Тема 1. Эконометрика как научная дисциплина
- •Вопросы для изучения:
- •Тема 2. Основные понятия теории вероятностей и статистики, применяемые в эконометрике
- •I. Схема проверки гипотезы о математическом ожидании нормальной св при известной дисперсии
- •II. Схема проверки гипотезы о математическом ожидании нормальной св при неизвестной дисперсии
- •III. Схема проверки гипотезы о величине дисперсии нормальной св
- •IV. Схема проверки гипотезы о равенстве двух нормальных св при известных дисперсиях
- •V. Схема проверки гипотезы о равенстве математических ожиданий двух нормальных св при неизвестных дисперсиях
- •VI. Схема проверки гипотезы о равенстве дисперсий двух нормальных св
- •VII. Схема проверки гипотезы о значимости коэффициента корреляции
- •Тема 3. Линейная модель парной регрессии и метод наименьших квадратов
- •Вопросы для изучения:
- •Тема 4. Экономическая и статистическая интерпретация линейной модели парной регрессии
- •Вопросы для изучения:
- •Тема 5. Линейная модель множественной регрессии и оценка ее параметров
- •Вопросы для изучения:
- •Тема 6. Оценка качества модели множественной регрессии
- •Вопросы для изучения:
- •Тема 7. Мультиколлинеарность
- •Тема 8. Гетероскедастичность.
- •Вопросы для изучения:
- •Тема 9. Автокорреляция
- •Тема 10. Фиктивные переменные
- •Тема 11. Нелинейные регрессии и их линеаризация
- •Тема 12. Модели с дискретной зависимой переменной
- •Тема 13. Модели панельных данных
- •Тема 14. Ошибки спецификации
- •Тема 15. Модели одномерных временных рядов
- •Вопросы для изучения:
- •Тема 16. Адаптивные модели временных рядов
- •Тема 17. Модели стационарных и нестационарных временных рядов
- •Вопросы для изучения:
- •Тема 18. Модели с лаговыми переменными
- •Тема 19. Понятие о системах эконометрических уравнений
- •Вопросы для изучения:
- •Тема 20. Методы оценки систем одновременных уравнений
- •Вопросы для изучения:
Тема 3. Линейная модель парной регрессии и метод наименьших квадратов
Аннотация. Данная тема раскрывает суть регрессионного анализа в эконометрике.
Ключевые слова. Модель регрессии, метод наименьших квадратов, остатки регрессии.
Методические рекомендации по изучению темы
Тема содержит лекционную часть, где даются общие представления по теме.
В качестве самостоятельной работы предлагается ознакомиться с решениями типовых задач, выполнить практические задания и ответить на вопросы для самоконтроля.
Для проверки усвоения темы имеется тест для самоконтроля.
Для подготовки к экзамену имеются контрольный тест.
Рекомендуемые информационные ресурсы:
1. http://tulpar.kpfu.ru/mod/resource/view.php?id=382
2. Эконометрика: [Электронный ресурс] Учеб.пособие / А.И. Новиков. - 2-e изд., испр. и доп. - М.: ИНФРА-М, 2011. - 144 с.: с. (http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=1#none) С. 28-46.
3.Уткин, В. Б. Эконометрика [Электронный ресурс] : Учебник / В. Б. Уткин; Под ред. проф. В. Б. Уткина. - 2-е изд. - М.: Издательско-торговая корпорация «Дашков и К°», 2012. - 564 с.
(http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=4#none) С. 323-338.
4. Валентинов, В. А. Эконометрика [Электронный ресурс]: Практикум / В. А. Валентинов. - 3-е изд. - М.: Дашков и К, 2010. - 436 с.
(http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=3#none) С. 38-99.
5.Эконометрика. Практикум: [Электронный ресурс] Учебное пособие / С.А. Бородич. - М.: НИЦ ИНФРА-М; Мн.: Нов.знание, 2014. - 329 с. (http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=4#none) С. 82-99.
6. Электронныйкурс “Econometrics and Public Policy (Advanced)”, Princeton University, URL: https://blackboard.princeton.edu/webapps /portal/frameset.jsp?tab_group=courses&url=%2Fwebapps%2Fblackboard%2Fexecute%2FcourseMain%3Fcourse_id%3D_214206_1
Глоссарий
Множественная регрессия представляет собой модель, где теоретическое (среднее) значение зависимой переменной Y рассматривается как функция нескольких независимых переменных X1, X2,...Xm.
Параметризация модели – выражение в математической форме взаимосвязи между переменными модели, формулирование исходных предпосылок и ограничений модели.
Парная регрессия представляет собой модель, где теоретическое (среднее) значение зависимой переменной Y рассматривается как функция одной независимой переменной X.
Спецификация модели - формулирование вида модели, исходя из соответствующей теории связи между переменными.
Цель регрессионного анализа – оценка функциональной зависимости между независимыми переменными X и условным математическим ожиданием зависимой переменной Y.
Вопросы для изучения:
Спецификация линейной модели парной регрессии.
Метод наименьших квадратов (МНК) – идентификация линейной модели парной регрессии.
Предпосылки МНК и свойства МНК-оценок.
Спецификация
линейной модели парной регрессии.
Основная
цель регрессионного анализа – оценка
функциональной зависимости между
независимыми переменными X и условным
математическим ожиданием зависимой
переменной Y.Простая (парная) регрессия
представляет собой модель, где
теоретическое (среднее) значение
зависимой переменной Y рассматривается
как функция одной независимой переменной
X:
 Множественная
регрессия представляет собой модель,
где теоретическое (среднее) значение
зависимой переменной Y рассматривается
как функция нескольких независимых
переменных X1, X2,...Xm:
Множественная
регрессия представляет собой модель,
где теоретическое (среднее) значение
зависимой переменной Y рассматривается
как функция нескольких независимых
переменных X1, X2,...Xm:
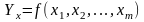
Спецификация модели - формулирование вида модели, исходя из соответствующей теории связи между переменными.Определяется состав переменных и математическая функция для отражения связи между ними.
Спецификация
линейной модели (уравнения) парной
регрессии: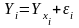
где Yi - фактическое значение зависимой переменной Y;
Yxi - теоретическое (среднее) значение зависимой переменной Y;
εi - случайная величина (остаток регрессии).
Теоретическое
уравнение регрессии (гипотетически для
генеральной совокупности):
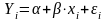
где α – свободный коэффициент;
β - коэффициент регрессии;
εi – случайное отклонение (возмущение).
Случайное отклонение включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Источники его присутствия в модели: спецификация модели, выборочный характер исходных данных, особенности измерения переменных.
Эмпирическое уравнение регрессии (для выборки наблюдений):
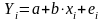
где а – эмпирическая (выборочная) оценка свободного коэффициента;
b - эмпирическая (выборочная) оценка коэффициента регрессии;
ei – эмпирическая (выборочная) оценка теоретического случайного отклонения ε (остаток регрессии).
Метод наименьших квадратов (МНК). Суть метода наименьших квадратов (МНК) - оценки параметров таковы, что сумма квадратов отклонений фактических значений зависимой переменной Yiот расчетных (теоретических) Yx минимальна:
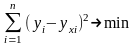
Оценкапараметров регрессии:
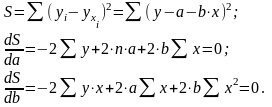
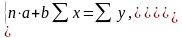
Предпосылки МНК и свойства МНК-оценок. Предпосылки МНК:
Математическое ожидание случайного отклонения εi равно нулю для всех наблюдений:
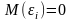
Дисперсия случайных отклонений εi постоянна. Выполнение предпосылки называется гомоскедатичностью, нарушение – гетероскедастичностью:
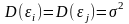
3.Случайные
отклонения εi
и εj
являются независимыми друг от друга
для i
≠ j.
Выполнение данной предпосылки говорит
об отсутствии автокорреляции, нарушение
– о присутствии автокорреляции:
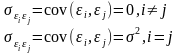
4.Случайное
отклонение должно быть независимо от
объясняющих переменных:
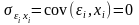
5.Модель линейна относительно параметров.
Если предпосылки МНК выполнены, то МНК-оценки регрессии обладают следующими свойствами:
1.Оценки являются
несмещенными:
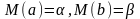
2. Оценки состоятельны,
так как их дисперсия при увеличении
выборки стремится к нулю: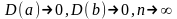
3.Оценки
эффективны, имеют наименьшую дисперсию
по сравнению с другими оценками, линейными
относительно зависимой переменной:
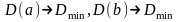
Вопросы и задания для самоконтроля
Что такое функция регрессии?
Чем регрессионная модель отличается от функции регрессии?
Каковы основные причины наличия в регрессионной модели случайного отклонения?
Как осуществляется спецификация модели?
В чем состоит различие между теоретическим и эмпирическим уравнениями регрессии?
В чем суть метода наименьших квадратов?
Каковы формулы расчета коэффициентов эмпирического парного линейного уравнения регрессии по МНК?
Каковы предпосылки МНК? Каковы последствия их выполнимости или невыполнимости?
Действительно ли оценки коэффициентов регрессии будут иметь нормальное распределение, если случайные отклонения распределены нормально?
Действительно ли в любой линейной регрессионной модели, построенной по МНК, сумма случайных отклонений равна нулю?
Задача 1.
При исследовании корреляционной
зависимости между ценой на нефть X
и индексом нефтяных компаний Y
получены следующие данные:
16,2;
4000;
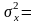 4;
4;
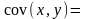 40.
40.
Задание: построить линейное уравнение регрессии Y на X.
Задача 2.
По выборке объема
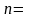 10
получены следующие данные:
10
получены следующие данные:
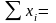 100;
100;
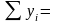 200;
200;
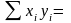 21000;
21000;
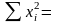 12000;
12000;
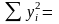 45000.
45000.
Задание: оценить с помощью МНК параметры линейного уравнения регрессии, найти выборочный коэффициент корреляции .
Лекция 4,5
