
- •Тема 1. Эконометрика как научная дисциплина
- •Вопросы для изучения:
- •Тема 2. Основные понятия теории вероятностей и статистики, применяемые в эконометрике
- •I. Схема проверки гипотезы о математическом ожидании нормальной св при известной дисперсии
- •II. Схема проверки гипотезы о математическом ожидании нормальной св при неизвестной дисперсии
- •III. Схема проверки гипотезы о величине дисперсии нормальной св
- •IV. Схема проверки гипотезы о равенстве двух нормальных св при известных дисперсиях
- •V. Схема проверки гипотезы о равенстве математических ожиданий двух нормальных св при неизвестных дисперсиях
- •VI. Схема проверки гипотезы о равенстве дисперсий двух нормальных св
- •VII. Схема проверки гипотезы о значимости коэффициента корреляции
- •Тема 3. Линейная модель парной регрессии и метод наименьших квадратов
- •Вопросы для изучения:
- •Тема 4. Экономическая и статистическая интерпретация линейной модели парной регрессии
- •Вопросы для изучения:
- •Тема 5. Линейная модель множественной регрессии и оценка ее параметров
- •Вопросы для изучения:
- •Тема 6. Оценка качества модели множественной регрессии
- •Вопросы для изучения:
- •Тема 7. Мультиколлинеарность
- •Тема 8. Гетероскедастичность.
- •Вопросы для изучения:
- •Тема 9. Автокорреляция
- •Тема 10. Фиктивные переменные
- •Тема 11. Нелинейные регрессии и их линеаризация
- •Тема 12. Модели с дискретной зависимой переменной
- •Тема 13. Модели панельных данных
- •Тема 14. Ошибки спецификации
- •Тема 15. Модели одномерных временных рядов
- •Вопросы для изучения:
- •Тема 16. Адаптивные модели временных рядов
- •Тема 17. Модели стационарных и нестационарных временных рядов
- •Вопросы для изучения:
- •Тема 18. Модели с лаговыми переменными
- •Тема 19. Понятие о системах эконометрических уравнений
- •Вопросы для изучения:
- •Тема 20. Методы оценки систем одновременных уравнений
- •Вопросы для изучения:
V. Схема проверки гипотезы о равенстве математических ожиданий двух нормальных св при неизвестных дисперсиях
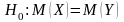
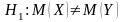
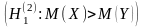 ;
;
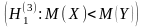 .
.
При этих условиях
в качестве критерия проверки
принимают СВ
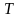 :
:
где
 - объемы выборок
- объемы выборок
 и
и
 соответственно
соответственно

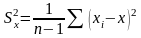 ,
,
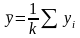 ;
; 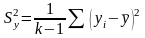 .
.
1. При
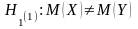 с помощью таблицы критических точек
распределения Стьюдента по заданному
уровню значимости α и числу степеней
свободы
с помощью таблицы критических точек
распределения Стьюдента по заданному
уровню значимости α и числу степеней
свободы
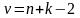 определяются критические точки
определяются критические точки
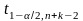 и
и
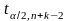 (
=
(
=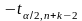 )
двусторонней критической области.
)
двусторонней критической области.
Если
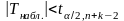 - нет оснований для отклонения Н0.
- нет оснований для отклонения Н0.
Если
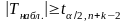 - Н0
отклоняется в пользу Н1(1).
- Н0
отклоняется в пользу Н1(1).
2. При
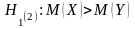 находят критическую точку
находят критическую точку
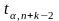 правосторонней критической области.
правосторонней критической области.
Если
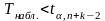 - нет оснований для отклонения Н0.
- нет оснований для отклонения Н0.
Если
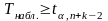 - Н0
отклоняется в пользу Н1(2).
- Н0
отклоняется в пользу Н1(2).
3.
При
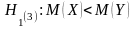 находят критическую точку левосторонней
критической области
находят критическую точку левосторонней
критической области
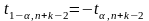 .
.
Если
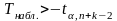 - нет оснований для отклонения Н0.
- нет оснований для отклонения Н0.
Если
 - Н0
отклоняется в пользу Н1(3).
- Н0
отклоняется в пользу Н1(3).
VI. Схема проверки гипотезы о равенстве дисперсий двух нормальных св
При сравнении двух экономических показателей иногда, в первую очередь, проводят анализ разброса значений рассматриваемых СВ. Например, при решении инвестирования в одну из отраслей остро стоит проблема риска вложений. При сравнивании уровня жизни двух стран среднедушевые доходы могут быть примерно одинаковы. Необходимо сопоставить разброс в доходах.
Анализ проводится путем сравнения дисперсий исследуемых СВ.
Пусть
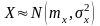 и
и
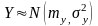 ,
причем их дисперсии
,
причем их дисперсии
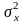 и
и
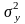 неизвестны. Выдвигается гипотеза о
равенстве дисперсий
и
.
неизвестны. Выдвигается гипотеза о
равенстве дисперсий
и
.
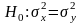
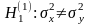
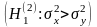 .
.
По независимым
выборкам
и
объемов
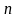 и
и
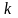 соответственно определяется:
соответственно определяется:
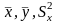 и
и
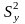 (для определенности пусть
(для определенности пусть
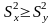 ,
в противном случае эти величины можно
переобозначить).
,
в противном случае эти величины можно
переобозначить).
В качестве критерия
проверки
принимают СВ
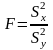 ,
,
определяемую
отношением большей исправленной
выборочной дисперсии к меньшей. Если
верна, то данная статистика
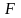 имеет
-
распределение Фишера с
имеет
-
распределение Фишера с
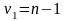 и
и
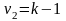 степенями свободы.
степенями свободы.
1. При
по таблицам критических точек распределения
Фишера по уровню значимости
и числам степеней свободы
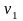 и
и
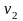 определяется критическая точка
определяется критическая точка
 .
.
Если
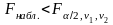 - нет оснований для отклонения
.
- нет оснований для отклонения
.
Если
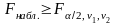 -
отклоняется
в пользу
.
-
отклоняется
в пользу
.
2. При
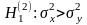 определяется критическая точка
определяется критическая точка
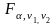 .
.
Если
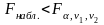 - нет оснований для отклонения
.
- нет оснований для отклонения
.
Если
 -
отклоняется
в пользу
.
-
отклоняется
в пользу
.
В основном, при проверке гипотезы о равенстве дисперсий в качестве альтернативной гипотезы в большинстве случаев используется гипотеза .
VII. Схема проверки гипотезы о значимости коэффициента корреляции
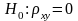
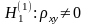 .
.
Для проверки
по выборке
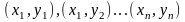 объема
строится статистика:
объема
строится статистика:
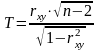
где
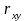 - выборочный коэффициент корреляции.
- выборочный коэффициент корреляции.
При справедливости
статистика
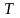 имеет распределение Стьюдента с
имеет распределение Стьюдента с
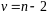 степенями свободы.
степенями свободы.
По таблице
критических точек распределения
Стьюдента по заданному уровню значимости
и числу степеней свободы
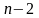 определяем критическую точку
определяем критическую точку
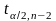 .
.
Если
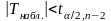 -
то нет оснований для отклонения
.
-
то нет оснований для отклонения
.
Если
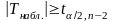 -
то
отклоняется
в пользу альтернативной гипотезы
.
-
то
отклоняется
в пользу альтернативной гипотезы
.
Если
отклоняется, то фактически это означает,
что коэффициент корреляции статистически
значим (существенно отличен от нуля).
Следовательно,
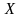 и
и
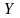 -
коррелированны, т.е. между ними существует
линейная связь.
-
коррелированны, т.е. между ними существует
линейная связь.
Вопросы и задания для самоконтроля
1. Как связаны между собой случайные величины, имеющие стандартизованное нормальное распределение, распределение Стьюдента, 2 и Фишера?
2. В чем заключаются несмещенность, эффективность и состоятельность статистических оценок?
3. Что такое точечная и интервальная оценка?
4. Что такое нулевая и альтернативная гипотезы?
5. Что такое статистический критерий, уровень значимости?
6. Какая случайная величина применяется в качестве критерия проверки гипотезы о величине дисперсии нормальной случайной величины?
7. Какая случайная величина применяется в качестве критерия проверки гипотезы о равенстве дисперсий двух нормальных случайных величин?
8. К проверке каких гипотез сводятся исследования среднего дохода населения и анализ разброса в уровне дохода?
Задача 1.
В
университете проведен анализ успеваемости
среди студентов и студенток за последние
25 лет. Случайные величины
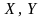 ,
представляющие их суммарный балл за
время учебы соответственно, имеют
нормальный закон распределения. Получены
следующие данные:
,
представляющие их суммарный балл за
время учебы соответственно, имеют
нормальный закон распределения. Получены
следующие данные:
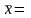 400,
400,
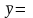 420,
Sx2=300,
Sy2=150.
420,
Sx2=300,
Sy2=150.
Задание: проверить,
можно ли на уровне значимости
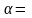 0,05
утверждать, что девушки в среднем учатся
лучше ребят.
0,05
утверждать, что девушки в среднем учатся
лучше ребят.
Задача 2. Точность работы станка-автомата, заполняющего пакеты со стиральным порошком, определяется совпадением веса пакетов. Дисперсия веса не должна превышать 25. По выборке из 20 пакетов определена исправленная дисперсия S2=30.
Задание: определить на уровне значимости 0,05 требуется ли переналадка станка.
Задача 3.
По двум независимым выборкам, объемы
которых
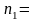 9
и
9
и
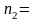 6,
найдены выборочные дисперсии Sx2=14,4
и Sy2=20,5
годовых дивидендов от вложений в отрасли
А и В соответственно.
6,
найдены выборочные дисперсии Sx2=14,4
и Sy2=20,5
годовых дивидендов от вложений в отрасли
А и В соответственно.
Задание: проверить при уровне значимости 0,05 гипотезу о равенстве рисков при вложении денег в обе отрасли.
Лекция 3
