
- •Тема 1. Эконометрика как научная дисциплина
- •Вопросы для изучения:
- •Тема 2. Основные понятия теории вероятностей и статистики, применяемые в эконометрике
- •I. Схема проверки гипотезы о математическом ожидании нормальной св при известной дисперсии
- •II. Схема проверки гипотезы о математическом ожидании нормальной св при неизвестной дисперсии
- •III. Схема проверки гипотезы о величине дисперсии нормальной св
- •IV. Схема проверки гипотезы о равенстве двух нормальных св при известных дисперсиях
- •V. Схема проверки гипотезы о равенстве математических ожиданий двух нормальных св при неизвестных дисперсиях
- •VI. Схема проверки гипотезы о равенстве дисперсий двух нормальных св
- •VII. Схема проверки гипотезы о значимости коэффициента корреляции
- •Тема 3. Линейная модель парной регрессии и метод наименьших квадратов
- •Вопросы для изучения:
- •Тема 4. Экономическая и статистическая интерпретация линейной модели парной регрессии
- •Вопросы для изучения:
- •Тема 5. Линейная модель множественной регрессии и оценка ее параметров
- •Вопросы для изучения:
- •Тема 6. Оценка качества модели множественной регрессии
- •Вопросы для изучения:
- •Тема 7. Мультиколлинеарность
- •Тема 8. Гетероскедастичность.
- •Вопросы для изучения:
- •Тема 9. Автокорреляция
- •Тема 10. Фиктивные переменные
- •Тема 11. Нелинейные регрессии и их линеаризация
- •Тема 12. Модели с дискретной зависимой переменной
- •Тема 13. Модели панельных данных
- •Тема 14. Ошибки спецификации
- •Тема 15. Модели одномерных временных рядов
- •Вопросы для изучения:
- •Тема 16. Адаптивные модели временных рядов
- •Тема 17. Модели стационарных и нестационарных временных рядов
- •Вопросы для изучения:
- •Тема 18. Модели с лаговыми переменными
- •Тема 19. Понятие о системах эконометрических уравнений
- •Вопросы для изучения:
- •Тема 20. Методы оценки систем одновременных уравнений
- •Вопросы для изучения:
I. Схема проверки гипотезы о математическом ожидании нормальной св при известной дисперсии
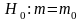
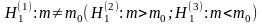
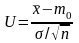 ,
где
,
где
 ,
,
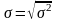 .
.
Пусть в качестве альтернативной рассматривается гипотеза:
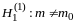 .
Тогда критические точки
.
Тогда критические точки
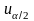 и
и
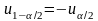 будут определяться по таблице значений
функции Лапласа из условия
будут определяться по таблице значений
функции Лапласа из условия
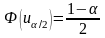
Если
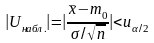 - нет оснований для отклонения
- нет оснований для отклонения
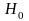 .
.
Если
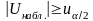 - гипотеза
отклоняется в пользу альтернативной
гипотезы
- гипотеза
отклоняется в пользу альтернативной
гипотезы
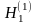 .
.
2. При
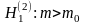 критическую точку
критическую точку
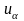 правосторонней критической области
находят из равенства
правосторонней критической области
находят из равенства
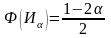
Если
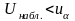 - нет оснований для отклонения
.
- нет оснований для отклонения
.
Если
 -
отклоняют в пользу
-
отклоняют в пользу
 .
.
3. При
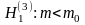 критическая точка
критическая точка
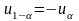 .
.
Если
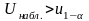 - нет оснований для отклонения
.
- нет оснований для отклонения
.
Если
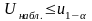 -
отклоняют в пользу
-
отклоняют в пользу
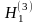 .
.
II. Схема проверки гипотезы о математическом ожидании нормальной св при неизвестной дисперсии
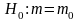
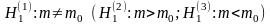 .
.
;
исправленная выборочная дисперсия
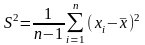 ;
;
стандартное
отклонение
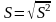 .
.
Далее строится
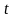 -
статистика:
-
статистика:
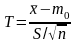 ,
имеющая при справедливости
распределение
Стьюдента с
,
имеющая при справедливости
распределение
Стьюдента с
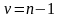 степенями свободы. Критическая область
строится в зависимости от вида
альтернативной гипотезы так же, как и
в предыдущем разделе.
степенями свободы. Критическая область
строится в зависимости от вида
альтернативной гипотезы так же, как и
в предыдущем разделе.
1. При
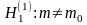 по таблице критических точек распределения
значимости
по таблице критических точек распределения
значимости
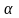 и числу степеней свободы
находятся критические точки:
и числу степеней свободы
находятся критические точки:
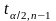 и
и
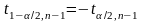 .
.
Если
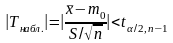 - нет оснований для отклонения
.
Если
- нет оснований для отклонения
.
Если
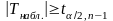 -
отклоняют в пользу
.
-
отклоняют в пользу
.
2. При
определяют критическую точку
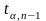 правосторонней критической области.
правосторонней критической области.
Если
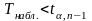 - нет оснований для отклонения
.
- нет оснований для отклонения
.
Если
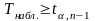 -
отклоняется в пользу
.
-
отклоняется в пользу
.
3. При
определяют критическую точку
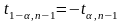 левосторонней критической области.
левосторонней критической области.
Если
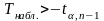 - нет оснований для отклонения
.
- нет оснований для отклонения
.
Если
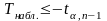 -
отклоняется в пользу
.
-
отклоняется в пользу
.
III. Схема проверки гипотезы о величине дисперсии нормальной св
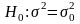
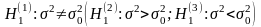 .
.
Для проверки
извлекается выборка объема
 вычисляются выборочное среднее
,
исправленная выборочная дисперсия
вычисляются выборочное среднее
,
исправленная выборочная дисперсия
 .
.
Тогда критерий
проверки
имеет вид:
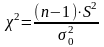 При справедливости
построенная статистика
При справедливости
построенная статистика
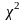 имеет
-
распределение с
степенями свободы.
имеет
-
распределение с
степенями свободы.
1. При
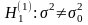 по таблице критических точек
по таблице критических точек
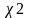 -
распределения по заданному уровню
значимости
и числу степеней свободы
находят критические точки
-
распределения по заданному уровню
значимости
и числу степеней свободы
находят критические точки
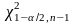 и
и
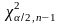 двусторонней критической области.
двусторонней критической области.
Если
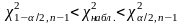 - нет оснований для отклонения
.
- нет оснований для отклонения
.
Если
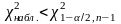 или
или
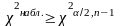 -
отклоняется в пользу
.
-
отклоняется в пользу
.
2.
При
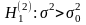 определяют критическую точку
определяют критическую точку
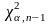 правосторонней критической области.
правосторонней критической области.
Если
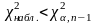 -
нет оснований для отклонения
.
-
нет оснований для отклонения
.
Если
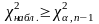 -
отклоняется в пользу
.
-
отклоняется в пользу
.
3. При
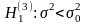 находят критическую точку
находят критическую точку
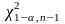 левосторонней критической области.
левосторонней критической области.
Если
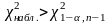 -
нет оснований для отклонения
.
-
нет оснований для отклонения
.
Если
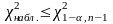 -
отклоняется в пользу
.
-
отклоняется в пользу
.
IV. Схема проверки гипотезы о равенстве двух нормальных св при известных дисперсиях
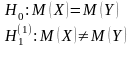
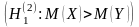
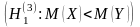 .
.
В качестве критерия проверки принимается СВ U:
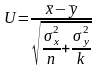
При справедливости СВ U ~ N (0, 1).
1. При
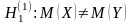 по таблице функции Лапласа определяют
2 критические точки
по таблице функции Лапласа определяют
2 критические точки
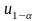 и
из условий:
и
из условий:
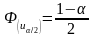 ,
,
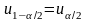 .
.
Если
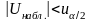 -
нет оснований для отклонения
-
нет оснований для отклонения
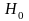 .
.
Если
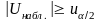 -
отклоняется в пользу
.
-
отклоняется в пользу
.
2. При
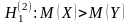 критическую точку
правосторонней критической области
находят их равенства:
критическую точку
правосторонней критической области
находят их равенства:
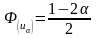 .
.
Если
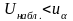 -
нет оснований для отклонения
.
-
нет оснований для отклонения
.
Если
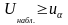 -
отклоняется в пользу
.
-
отклоняется в пользу
.
3. При
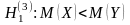 критическая точка
левосторонней критической области
определяется из соотношения
.
критическая точка
левосторонней критической области
определяется из соотношения
.
Если
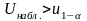 -
нет оснований для отклонения
.
-
нет оснований для отклонения
.
Если
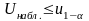 -
отклоняется в пользу
.
-
отклоняется в пользу
.
