Тема 18. Модели с лаговыми переменными

Аннотация. Данная тема раскрывает особенности моделей с лаговыми переменными и методы их оценивания.

Ключевые слова. Модель с распределенным лагом, метод Алмон, метод Койка, модель частичной корректировки, модель адаптивных ожиданий.

Методические рекомендации по изучению темы

Тема содержит лекционную часть, где даются общие представления по теме.
В качестве самостоятельной работы предлагается выполнить практические задания и ответить на вопросы для самоконтроля.
Для проверки усвоения темы имеется тест для самоконтроля.
Для подготовки к экзамену имеется контрольный тест.

Рекомендуемые информационные ресурсы:

1. http://tulpar.kpfu.ru/mod/resource/view.php?id=11766

2. Эконометрика: [Электронный ресурс] Учеб. пособие / А.И. Новиков. - 3-e изд., испр. и доп. - М.: ИНФРА-М, 2014. - 272 с.: (http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=1#none) С. 138-146.

3. Эконометрика. Практикум: [Электронный ресурс] Учебное пособие / С.А. Бородич. - М.: НИЦ ИНФРА-М; Мн.: Нов. знание, 2014. - 329 с. (http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=4#none) С.273-276.

4. Электронный курс “Time Series Econometrics”, Princeton University, URL: http://sims.princeton.edu/yftp/Times05/;https://blackboard.princeton.edu/webapps/portal/frameset.jsp?tab_group=courses&url=%2Fwebapps%2Fblackboard%2Fexecute%2FcourseMain%3Fcourse_id%3D_52968_1.

Глоссарий

Статическая эконометрическая модель – это модель, построенная по данным временного ряда, которая не содержит лаговые значения экзогенных и (или) эндогенных переменных.

Динамическая эконометрическая модель – это модель, которая в данный момент времени t учитывает значения входящих в нее переменных, относящиеся как к текущему, так и к предыдущим моментам времени.

Лаговые переменные - это переменные, влияние которых характеризуется определенным запаздыванием во времени.

Модель с распределенным лагом - это эконометрическая модель, которая содержит в качестве лаговых переменных лишь независимые (объясняющие) переменные.

Модель адаптивных ожиданий - это эконометрическая модель, в которой применяется процедура корректировки ожиданий, когда в каждый момент времени реальное значение переменной х сравнивается с её ожидаемым значением.

Модель частичной корректировки – это эконометрическая модель, в которой поведенческое уравнение определяет не фактическое значение y_t, а её желаемый (целевой) уровень .

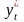Вопросы для изучения

1. Статические и динамические модели.

2. Модели с распределенным лагом.

3. Модель частичной корректировки и модель адаптивных ожиданий.

Статические и динамические модели. Эконометрическая модель, построенная по данным временного ряда, является статической, если она не содержит лаговые значения экзогенных и (или) эндогенных переменных.

Эконометрическая модель является динамической, если в данный момент времени t она учитывает значения входящих в нее переменных, относящиеся как к текущему, так и к предыдущим моментам времени, то есть отражает динамику переменных в каждый момент времени. Различают два типа динамических моделей.

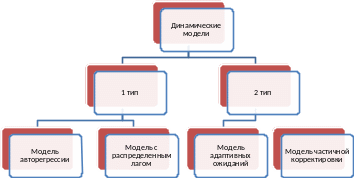
Рис. 18.1. Типы динамических моделей.

Модели с распределенным лагом. Переменные, влияние которых характеризуется определенным запаздыванием, называются лаговыми переменными. Модели с распределенным лагом содержат в качестве лаговых переменных лишь независимые (объясняющие) переменные: 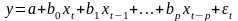. Модель говорит о том, что, если в некоторый момент времени t происходит изменение х, это изменение будет влиять на значение Y в течение р последующих моментов времени. Коэффициент b₀ называется краткосрочным мультипликатором, т.к. он характеризует изменение среднего значения Y при единичном изменении х в тот же самый момент времени. Сумма 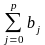называется долгосрочным мультипликатором; он характеризует изменение Y под воздействием единичного изменения х в каждом из моментов времени. Любая сумма 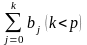называется промежуточным мультипликатором.

Достоинства метода Алмон: универсальность, применимость для моделирования процессов с разнообразными структурами лагов. При малых k (2 или 3) можно построить модели с распределенным лагом любой длины. Ограничения метода Алмон: величина р должна быть известна заранее. При этом приходится задавать максимально возможную величину лага. Выбор меньшего лага, чем его реальное значение, приведет к неверной спецификации модели, невозможности обеспечить случайность остатков, поскольку влияние значимых факторов будет выражено в остатках. Оценки параметров при этом окажутся неэффективными и смещенными. Включение в модель большей величины лага, чем его реальное значение, снижает эффективность оценок из-за наличия статистически незначимых факторов. Метод Койка применяется в модели с бесконечным лагом, по модели авторегрессии ,

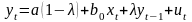определив её параметры, находим λ, а, b₀исходной модели, а затем и параметры .

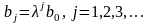Модель частичной корректировки и модель адаптивных ожиданий. Модель адаптивных ожиданий заключается в простой процедуре корректировки ожиданий, когда в каждый момент времени реальное значение переменной х сравнивается с её ожидаемым значением. Если реальное значение оказывается больше, то ожидаемое в следующий момент значение корректируется в сторону его увеличения, если меньше – то в сторону уменьшения. Предполагается, что размер корректировки пропорционален разности между реальным и ожидаемым значениями переменной. Таким образом, основную идею можно записать формулой: .

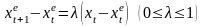В модели частичной корректировки поведенческое уравнение определяет не фактическое значение y_t, а её желаемый (целевой) уровень :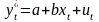 . В модели предполагается, что фактическое приращение зависимой переменной пропорционально разнице между её желаемым уровнем и значением в предыдущий период. Модель частичной корректировки: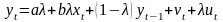 также является моделью авторегрессии.