Вхимии почв: уравнения сорбции
•Степенная функция
Q mCn |
Уравнение Фрейндлиха |
• Логистическая
A A |
|
KС |
|
|
л |
Уравнение Ленгмюра |
|
|
KС |
||
1 |
Аналогичные уравнения Моно, |
||
|
|
л |
Михаэлиса-Ментен и др. |
|
|
|
|
•Гауссиада (агрохимия, биология почв, статистика и др.)
В биологии почв, экологии: физический смысл параметров гауссиады
• В уравнении гауссиады
|
|
|
|
x b2 2 |
|
|
|
b1 |
exp |
|
|
|
|
|
|
b3 |
|||||||
|
|
|
|
|
|
||
|
|
|
|
|
b1 – обилие вида
b2 – биологический оптимум
b3 – толерантность (мера экологической амплитуды)
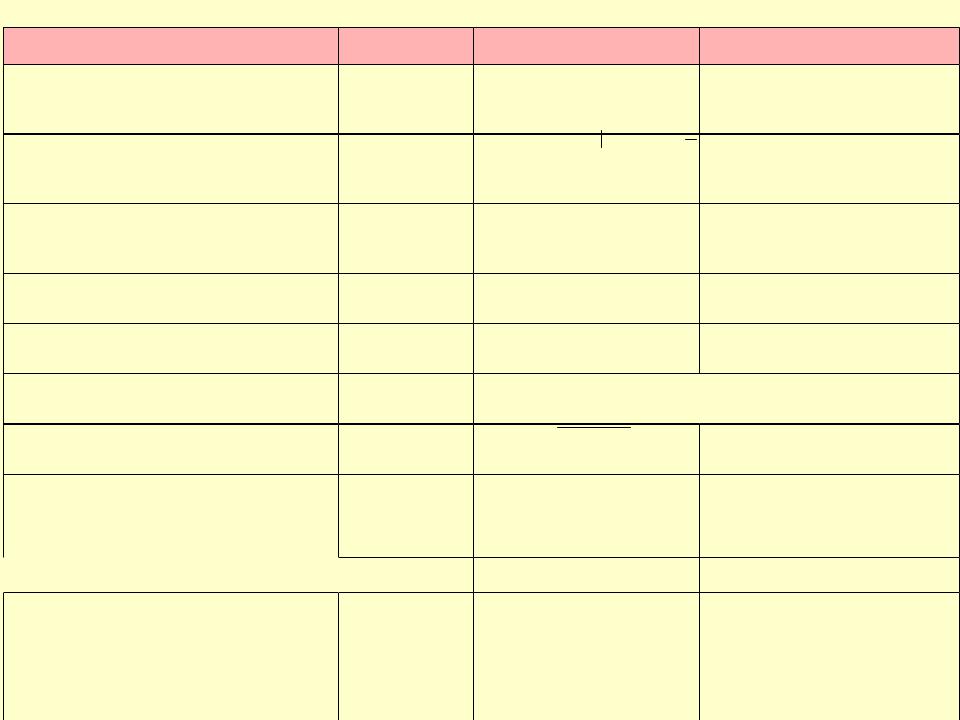
Раздел почвоведения, использвание
Накопление почвенного органического вещества.
Почвоведение Основная гидрофизическая
характеристика.
Почвенная гидрология Основная гидрофизическая
характеристика.
Почвенная гидрология Моментальная адсорбция
Химия почв Моментальная адсорбция
Химия почв Поглощение веществ растением.
Агрохимия Кинетика 1-го порядка.
Химия, физика почв Кинетика 2-го порядка.
Кинетика нулевого порядка
Логарифмическая зависимость урожая от химических веществ (удобрений)
Функции в почвоведении |
|||||||||||||||||||||
Функция |
Вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Автор |
|
Название |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение Костычева-Иенни по |
||
Показательная |
|
|
y t |
y0 |
1 |
|
e |
kt |
|||||||||||||
|
|
|
|
|
накоплению органического |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
вещества почв |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
||||
Степенная |
|
i r |
|
|
PдляР |
|
|
|
|
|
|
Brooks and Corey, 1964 |
|||||||||
|
|
|
|
к c |
|
|
|
|
|
|
|
|
к с |
|
|||||||
|
Se |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s r |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||
|
|
|
1дляР |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
к с |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Логистическая |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
m |
|
|
ван Генухтеном (van Genuchten, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дляPк c 1980 |
|||||
|
|
i |
r |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
n |
||||||||||
|
Se |
|
|
|
|
1 |
( P |
|
|
) |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
s |
r |
|
|
|
|
|
к с |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|||||||
|
|
|
|
|
|
дляР |
|
|
|
|
|
||||||||||
Степенная |
|
|
|
|
|
sк с |
|
|
|
|
|
|
|
|
|
Уравнение Фрейндлиха |
|||||
Логит функция
Логит функция
Экспоненциальн
ая Логит функция
Линейная
Q mCn
A A KС
л
1 KС
л
Jr Jmax Kmc cmin
1 Kmc
Ci C0 exp( k1t)
Ci |
|
|
C0 |
|
|
|
1 |
k2 C0 |
t |
||||
|
||||||
Уравнение Ленгмюра.
Уравнение Михаэлиса-Ментен
Логарифмичес
кая
Ci C0 k0t
гдеlgА –Aмаксимальныйy lg A b(урожай,x c) у
– урожай при внесении того или иного химического вещества в почву в количестве х, и b – фактор действия этого вещества,
Уравнение Макса Айдхарда Альфреда Мичерлиха
А если мы не знаем вида? Или функция очень сложная? С несколькими экстремумами?
•Например, кривая сорбции паров воды.
•Это S-образная функция. У нас не было функций такого вида. Что делать в этом случае?
•Надо использовать принцип пошаговой регрессии, начиная с полинома.
Общие правила подбора функций для экспериментальных данных
• Определите вид функции (выбор из VШ типов:
возрастающие, убывающие, с одним максимумом, минимумом….).
•Задайте функцию с наименьшим числом параметров по правилу: n=b+3, где n -число параметров, b – число пар «функция- аргумент».
•Испытайте другой тип функции и по критерию Вильямса-Клюта докажите различия и выберите лучшую.
•Попытайтесь выяснить и оценить физическое значение параметров.
Новая тема
«Использование физически обоснованных моделей
•Балансовые и имитационные (с сеточной схемой расчета) модели;
•Препроцессор и постпроцессор;
•Формулировка задачи; пространственные и временные границы моделируемого процесса;
•Задание почвенных свойств и характеристик. Графический редактор;
•Постпроцессор. Выдачи модели.
Работа с физически обоснованными моделями Модель водо- и солеобмена почв HYDRUS
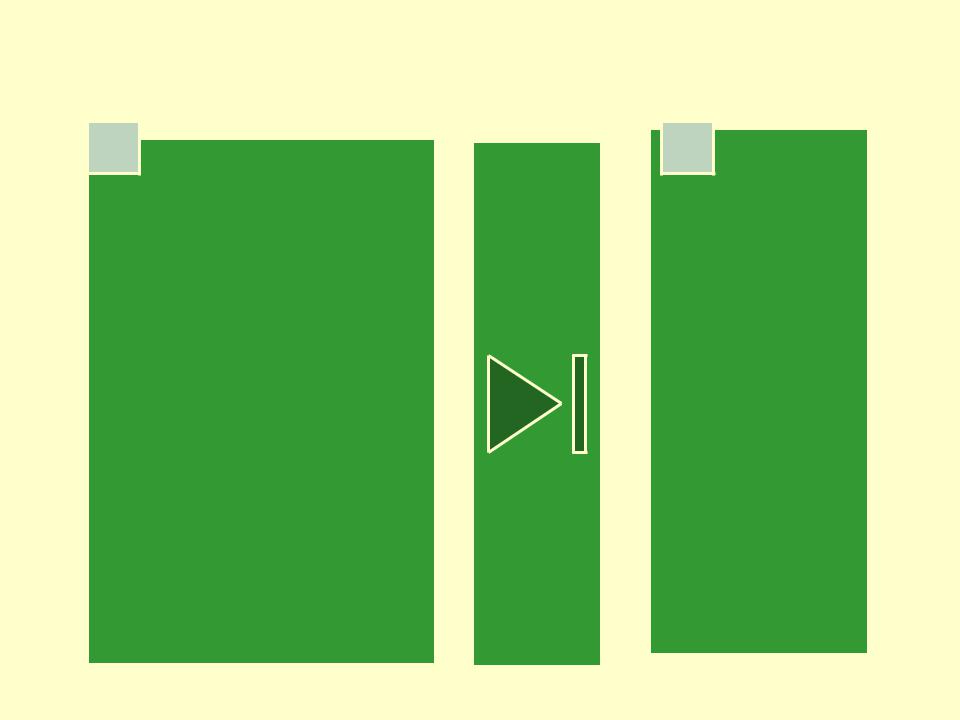
Структура моделей
•Препроцесс
ор
•Пространственные
данные
•Временные
•Задание выдач
•Почвенные данные
•ОГХ
•Кф - фильтрация
•Метео-
•Пост
проце
ссор
•Выдачи
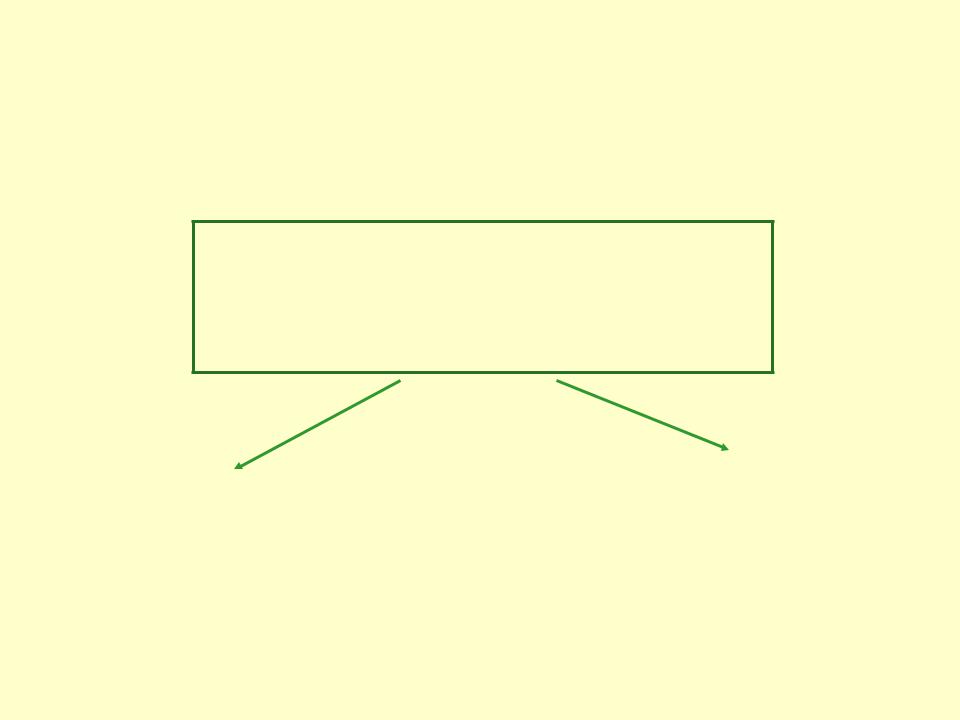
Типы наиболее употребительных моделей
Физически обоснованные модели
|
|
Имитационные |
|
балансовые |
|||
|
(с сеточной схемой расчета) |
||
|
|
2 типа моделей:
балансовые и имитационные (механистические, «сеточные» модели, физически обоснованные).
1.Устройство моделей. Их характерные признаки.
2.Препроцессор моделей
3.Недостатки каждого из типов.