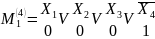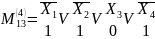Основные законы алгебры логики.
Одинарные законы.
X v 0 = X X ^ 0 = 0
X v 1 = 1 X ^ 1 = X
X v X = X X ^ X = X
X
v
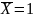X
^
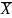= 0
.
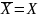Отметим, что двойное инвертирование не только одной переменной, а логической формулы дает нам тоже значение формулы.
Отметим отдельно свойство конъюнкции:
X ^ 1 = Х X ^ 0 = 0
Эти свойства говорят о том, что элемент «И» можно использовать в качестве электронного ключа, который пропускает или не пропускает входной сигнал Х на выход в зависимости от присутствия на втором входе единицы или нуля.
Комбинационные законы.
В логике операции дизъюнкции и конъюнкции является двойственными, это означает, что если записан закон относительно дизъюнкции и конъюнкции при замене этих операций на двойственные мы также получаем законы Булевой алгебры.
Переместительный:
;
.
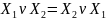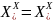Сочетательный:
.
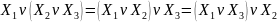Например, при использовании двухвходовых схем.
Рисунок 1.3.1
.
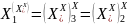Дистрибутивный:
;
.
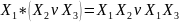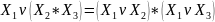Следующие два закона по сути дела являются следствием дистрибутивного, однако в логике имеют свое название из – за применения в методах минимизации.
Закон поглощения.
;
.
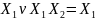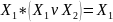Говорят,
что
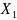– поглощает
второй член
.
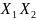Что бы понять, как использоваться этот закон докажем:
.
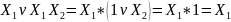Если имеется дизъюнкция двух конъюнкций и одна из них полностью входит во вторую (общий сомножитель), то эта конъюнкция поглощает вторую.
Закон склеивания.
;
.
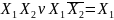Говорят,
что произошло склеивание по переменной
.
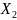Для того, что бы понять, как работать с этим законом, докажем:
.
Анализируя доказательство, сделаем вывод:
Склеивание двух конъюнкций с одинаковым количеством одинаковых элементов может происходить только по одной переменной, которая в одну конъюнкцию входит прямо, а в другую с инверсией.
Все остальные члены конъюнкции должны быть одинаковы (представлять общий сомножитель).
Результатом склеивания является общий сомножитель.
Пример:
;
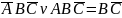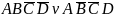– склеивание
не возможно
Закон Де Моргана.
;
.
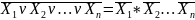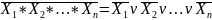Отрицание дизъюнкции есть конъюнкция отрицаний.
Отрицание конъюнкции есть дизъюнкция отрицаний.
Этот закон справедлив не только для одной переменной, но и для сложных выражений, например, конъюнкций, связанных дизъюнкцией и наоборот.
Пример:
=
;
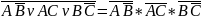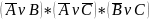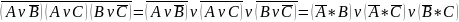
Аналитическое представление переключательных функций.
Понятие конституенты единицы и нуля.
Поставим перед собой задачу аналитической записи в таблице истинности единицы на конкретном наборе, причем запись необходимо осуществить с помощью элементов базиса Буля. Такая возможность имеется, если воспользоваться понятием «Конституента единицы».
Определение: Конституента единицы – специальная переключательная функция, которая равна единице только на одном наборе переменных.
Записывается конституента единицы через конъюнкцию входных переменных, с использованием инверсии. Для функции n переменных существует крнституента единицы.
В качестве примера запишем конституенты единицы для функции 2-yx переменных.
n=2,
то
.
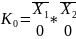
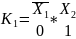
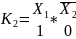
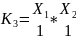
Правило: чтобы записать конституенту единицы n переменных на m-ом наборе необходимо записать конъюнкцию n переменных под ней двоичный эквивалент номера набора m и поставить отрицания под теми переменными, которым в двоичном числе соответствуют нули.
В качестве примера запишем конституанты единицы, 5-ти переменных на 5-ом и 25-ом наборах.
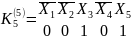
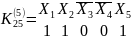
Можно проводить синтез переключательной функции и по нулям. Для этого вводится понятие «Конституенты нуля». Записывается эта конституента через дизъюнкцию входных переменных, с применением инверсии.
Запишем конституанты нуля для 2-ух переменных:
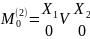
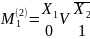
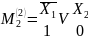
Правило: чтобы записать конституанту нуля n переменных на m-ом наборе необходимо записать дизъюнкцию n переменных под ней двоичной эквивалент номера набора и поставить знаки отрицания над аргументами, которым в двоичном числе соответствует единица.
Пример:
