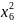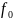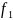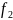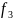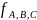Алгебра логики в задачах синтеза функциональных узлов дискретной техники Содержание

1. Основы алгебры логики

   1. Понятие переключательной функции, наборы, таблицы истинности ……………………………………………………………………………………......3

   2. Переключательная функция двух переменных. Функциональные полные базисы………………………………………………………………………………...6

   3. Основные законы алгебры логики …………………………………………………9

2. Аналитическое представление переключательных функций

   1. Понятие конституенты единицы и нуля …………………………………………..11

   2. Понятие совершенных дизъюнктивных нормальных форм (СДНФ) и совершенных конъюнктивных нормальных форм (СКНФ)………………...……12

   3. Переход от СДНФ и СКНФ в базис Шеффера и Вебба………………………......14

3. Минимизация переключательных функций

   1. Минимизация переключательных функций ………………………………………17

   2. Минимизация переключательных функций методом Карно – Вейча…………...21

   3. Минимизация не полностью определённых переключательных функций……..27

4. Синтез функциональных узлов комбинационного типа

   1. Классификация интегральных схем………………………………………………..29

   2. Двоичные дешифраторы……………………………………………………………30

   3. Двоичный шифратор………………………………………………………………..35

   4. Мультиплексоры и демультиплексоры……………………………………………37

   5. Одноразрядные сумматоры………………………………………………………...40

5. Синтез автоматов с памятью

   1. Функциональные узлы последовательного типа (Автоматы с памятью)……….45

   2. Асинхронный и синхронный RS – триггер………………………………………..47

   3. D – триггер…………………………………………………………………………..52

   4. Т – триггер…………………………………………………………………………...54

   5. JK – триггер………………………………………………………………………….55

   6. Двоичный счетчики…………………………………………………………………58

   7. Пересчетные схемы……………………………………………………………….62

   8. Параллельные регистры………………………………………………………….65

   9. Последовательные регистры………………………………………………...…..69

Список использованных источников……………………………………………………....72

1. Основы алгебры логики.

   1. Понятие переключательной функции, наборы, таблицы истинности.

Основные положения и законы алгебры логики, разработаны математиком Булем, поэтому ее часто называют «Булевой алгеброй». Булева алгебра оперирует понятием переключательных функций.

Булевой или переключательной называется функция, которая как и ее аргументы может принимать только два значения «ноль» и «единица». В связи с тем, что цифровая техника также оперирует с нулем или единицей на входах цифровых устройств, а на выходе так же получает значение ноль или единица, цифровые схемы можно описывать формально переключательными функциями.

f( )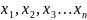

Принято конкретное значение аргументов (входных переменных) называть набором. Все наборы номеруются, начиная с нулевого. Номер набора равен двоичному числу, образованному значениями аргументов.

Для функции n – аргументов существует 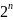возможных наборов. Например если n=2, то количество возможных наборов 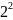=4, то есть для двух переменных 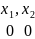– нулевой набор, 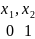– первый набор, 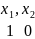– второй набор, 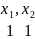– третий набор.

Для функции n аргументов последний набор всегда единичный, а начинаются наборы всегда с нулевого.

Говорят, что Булева функция определена на наборах, то есть для конкретной переключательной функции известно какие значения она принимает на всех наборах. Для наборов может существовать 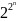различных переключательных функций.

Переключательная функция также имеет свой номер. Номер переключательной функции равен двоичному числу, образованному значениями функций на наборах, начиная с нулевого. Этот номер легко определить по таблице истинности, которой описывается переключательная функция.

Например, логическая операция конъюнкция (логическое умножение).

Составим таблицу истинности для конъюнкции двух переменных:

Таблица 1.1.1

	0	0	1	1
	0	1	0	1
f( )	0	0	0	1

Конъюнкция двух переменных как переключательная функция имеет номер один.

Составим таблицу истинности для трех переменных:

Таблица 1.1.2

	0	0	0	0	1	1	1	1
	0	0	1	1	0	0	1	1
	0	1	0	1	0	1	0	1
f( )	0	0	0	0	0	0	0	1

Можно проводить и обратную операцию, то есть по номеру функции строить таблицы истинности.

Например, получить таблицу истинности функции двух переменных, шестой функции 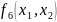. Двоичный эквивалент десятичного числа 6 в четырех разрядах – 0110.

Таблица 1.1.3

	0	0	1	1
	0	1	0	1
	0	1	1	0

Рассмотрим возможные наборы и возможные функции одной переменной и дадим им логическое обоснование. n=1 следовательно количество наборов 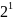= 2 (0 и 1), но количество функций 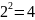. Построим таблицу истинности.

Таблица 1.1.4

x	0	1	Название функций
	0	0	Константа «нуля»
	0	1	Повторение «Х»
	1	0	Инверсия «Х»
	1	1	Константа «единицы»

Анализируя значения возможных функций одной переменной, отметим, что только одна из них имеет применение в технике, а именно «инверсия х» .

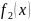Существует специальный элемент, который реализует эту функцию. Его графическое изображение:

Рисунок 1.1.1

Читается «Не Х», а схема в технике называется «НЕ» или инвертор.

Пример:

В качестве примера проведем синтез переключательной функции, то есть построим таблицу истинности для устройства голосования.

Пусть голосует три человека нажатием кнопки. Если решение проходит, то на выходе устройства должна быть единица, которая, например, зажигает лампочку. Решение принимается большинством голосов.

Голосующие представляют собой три переменных A, B и C на входе устройства и каждый голосующий может проголосовать по – разному следовательно возможных комбинаций голосования 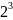. Записываем восемь наборов в таблицу переменных. Осталось только проставить единицы для тех наборов, которые удовлетворяют логике задачи.

A	B	C
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Выводы:

• Любую переключательную функцию, а следовательно любое дискретное устройство можно описать таблицей истинности по заданной логике работы.

• Количество переменных n переключательной функции или входных сигналов устройства формально определяет количество возможных комбинаций входных сигналов, которое равно .

• Значение функции или значение выхода устройства определяется по логике работы и, может иметь свой номер.

В нашем примере синтезировано устройство трех переменных, что соответствует переключательной функции 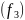с номером 10111 (23), то есть .
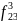
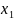
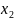
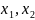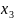
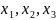