Санкт-Петербургский государственный политехнический университет

Институт энергетики и транспортных систем

Кафедра «Теоретические основы электротехники»

К У Р С О В О Й П Р О Е К Т

Расчеты электромагнитных полей и электромагнитных параметров электротехнических устройств

по дисциплине «Теоретические основы электротехники»

Выполнил

Студент группы 33213/1 П.Д.Никитин

Руководитель

доцент, к.т.н. А.Н.Модулина

«_____» _____________________2014 г.

Санкт-Петербург

2014 г.

Санкт-Петербургский государственный политехнический университет

Задание на выполнение курсового проекта

студенту группы 33213/1 Никитину П.Д.

1. Тема проекта: Расчеты электромагнитных полей и электромагнитных параметров электротехнических устройств

2. Срок сдачи студентом законченного проекта 17 декабря 2014 г.

3. Исходные данные к проекту:

3.1. Сферический конденсатор;

3.2 Линейный провод, распложенный вблизи проводящего экрана;

3.3. Устройство с ферромагнитным сердечником.

4. Содержание пояснительной записки:

4.1. Введение;

4.2. Основная часть.

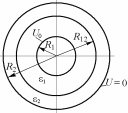
4.2.1. Расчет электростатического поля сферического конденсатора, сечение которого изображено на рис. Z-1

Рис. Z-1

1. Вывести выражения потенциала и напряженности электростатического поля в пространстве между обкладками сферического конденсатора (см. рис. Z-1) с радиусами R₁=2,5 см и R₂=6 см, построить графики полученных зависимостей U(r) и E(r) в случаях, когда:

1.1. между электродами помещена двухслойная изоляция с абсолютными диэлектрическими проницаемостями слоев 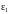 =9 ₀ и 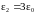, радиус поверхности раздела слоев диэлектрика равен R₁₂=4 см, внутренняя обкладка конденсатора подключена к источнику ЭДС с напряжением U₀=300 В, внешняя заземлена (U₂=0);

1.2. двухслойная изоляция заменена однородным диэлектриком с проницаемостью 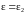, замена произведена при подключенном к внутреннему электроду источнике ЭДС;

1.3. двухслойная изоляция заменена однородным диэлектриком с проницаемостью 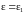, замена произведена после отключения внутреннего электрода от источника ЭДС.

Во всех рассмотренных случаях определить полные заряды q каждого из электродов и поверхностную плотность зарядов  на них.

2. Полагая напряжение между электродами u₁₂=U₁–U₂ фиксированным и равным U₀, получить и построить зависимости напряжений слоев диэлектрика u_I=U₁–U₁₂ и u_II=U₁₂–U₂, максимальной напряженности поля E_max, зарядов q каждого из электродов и поверхностной плотности зарядов  на них, а также емкости системы C от ₁.

3. Определить оптимальное значение диэлектрической проницаемости ₂ внешнего слоя изоляции, при котором максимальные величины напряженности во внутреннем и внешнем слоях диэлектрика одинаковы.

4.2.2. Расчет плоскопараллельного электростатического поля между линейным заряженным проводом и проводящим экраном

а)	б)

Рис. Z-2

Провода несимметричной трехфазной системы расположены в однородной среде с диэлектрической проницаемостью ₀ вблизи проводящего экрана. Минимальное расстояние от провода до экрана равно d. Один из проводов (1), показанный на рис. Z-2,а, имеет линейный заряд , заряды проводов 2 и 3, расположенных относительно 1-го в соответствии с рис. Z-2,б, равны нулю. Радиусы проводов одинаковы и равны R=0,1d.

1. Построить картину плоскопараллельного электростатического поля, создаваемого 1-м проводом (см. рис. Z-2,а). При построении картины поля радиусом провода пренебречь. Принять число линий равного потенциала, включая границу, n=5 и число трубок потока вектора напряженности m= 9. Определить распределение индуцированного заряда  по поверхности экрана.

2. Рассчитать емкость 1-го провода относительно экрана на единицу длины системы. Сопоставить полученное значение емкости с емкостью

а) такого же провода, расположенного на расстоянии d от плоской проводящей поверхности,

б) цилиндрического конденсатора с радиусом внутренней жилы R₁=R, внутренним радиусом оболочки R₂=d и диэлектрической проницаемостью диэлектрика ₀.

3. Определить величины потенциалов каждого из проводов трехпроводной линии, приняв а=3, b= 4.

4. Определить емкость провода трехфазной транспонированной линии на единицу ее длины.

4.2.3. Расчет магнитного поля и определение параметров устройства с ферромагнитным сердечником

a= 6; b= 8; c= 20; d=2; f=4; g=10

Рис. Z-3

Плоскопараллельное магнитное поле создается в межполюсном пространстве системой обмоток, обтекаемых током i = 1 А, витки которых w = 100 равномерно распределены по сечению (рис. Z-3,а).

1. Принимая магнитную проницаемость материала сердечника _Fe = ∞ и положив толщину обмотки t=0, построить картину магнитного поля, используя:

а) графический метод;

б) результат расчета «вручную» распределения скалярного магнитного потенциала методом конечных разностей.

2. С помощью программы “POLUS” выполнить расчет распределения скалярного магнитного потенциала и функции потока и построить картины полей для толщины обмотки t = 0; t=a/2 и t=a. По построенным картинам полей определить индуктивность обмотки. Построить зависимость индуктивности от ширины обмотки L(t). Размеры магнитной системы в сантиметрах приведены на рис. Z-3,б.

4.3. Заключение.

4.4. Список использованных источников.

4.5. Приложения.