Кривые второго порядка

Уравнение второй степени относительно двух переменных

при разных значениях коэффициентов описывает четыре вида линий на плоскости: окружность, эллипс, гиперболу и параболу. Это уравнение называется общим уравнением кривых второго порядка.

Окружность

Окружностью называется геометрическое место точек, равноудаленных от данной точки (центра).

Нормальное уравнение окружности имеет вид:

,

где - координаты центра окружности; - радиус окружности.

Эллипс

Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух данных точек, называемых фокусами, есть постоянная величина , большая, чем расстояние между фокусами .

Каноническое уравнение эллипса имеет вид

где , если и фокусы находятся на оси . Параметры называются полуосями эллипса. Отношение называется эксцентриситетом эллипса.

Расстояние от точки эллипса до его фокусов (фокальные радиусы) находятся по формулам: .

Гипербола

Гиперболой называется геометрическое место точек, разность расстояний от которых до двух данных точек (фокусов), есть постоянная величина , причем , где - расстояние между фокусами.

Каноническое уравнение гиперболы, симметричной относительно осей координат, имеет вид , где .

Параметр называется вещественной полуосью гиперболы и представляет собой расстояние от начала координат до вершины гиперболы, параметр называется мнимой полуосью .

Эксцентриситетом гиперболы называется величина .

Расстояния от точки гиперболы до фокусов (фокальные радиусы) определяются по формулам: .

Прямые, заданные уравнениями являются асимптотами гиперболы.

Парабола

Параболой называется геометрическое место точек, одинаково удаленных от данной точки (фокуса) и данной прямой (директрисы).

Каноническое уравнение параболы, проходящей через начало координат и симметричной относительно оси имеет вид: .

Уравнение вида описывает параболу, симметричную относительно оси .

Фокальный радиус точки , т.е. ее расстояние до фокуса на оси , находится по формуле .

Парабола, ось которой параллельна оси , описывается уравнением .

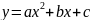Задания:

1. Найти координаты центра и радиус окружности . Построить окружность.

2. Составить уравнение окружности, проходящей через точку пересечения окружности с прямой и точку .

3. Составить каноническое уравнение эллипса, проходящего через точки .

4. Написать каноническое уравнение эллипса, если малая полуось равна 5, а эксцентриситет равен .

5. Найти расстояние между фокусами и эксцентриситет гиперболы

6. Составить уравнение гиперболы, если ее асимптоты заданы уравнениями и гипербола проходит через точку

7. Составить уравнение параболы, если ее фокус находится в точке пересечения прямой с осью

8. Составить каноническое уравнение параболы, вершина которой лежит в начале координат и которая проходит через точку - ось симметрии.