1 Прямая на плоскости

Если в системе координат на прямой, перпендикулярной нормальному вектору , задана точка , то выбрав на этой прямой произвольную точку , вектор можно записать через координаты в виде

И спользуя условие перпендикулярности двух векторов , получаем уравнение (1)

которое носит название уравнения прямой, проходящей через данную точку.

После раскрытия скобок уравнение (1) принимает вид:

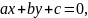(2)

где . Уравнение (2) называется общим уравнением прямой на плоскости.

Если , или

, которое носит название уравнения прямой с угловым коэффициентом, а величина определяет ординату точки пересечения прямой с осью .

Если на плоскости заданы две точки , то уравнение пучка прямых имеет вид: (3)

(4)

Уравнение (4) называется уравнением прямой, проходящей через две заданные точки.

Возьмем точки и подставим в уравнение (4). Получим – уравнение прямой в отрезках на осях. (5)

Если две прямые заданы уравнениями , то тангенс угла между ними вычисляется по формуле

(6)

В случае задания двух прямых общими уравнениями прямых можно выразить косинус одного из смежных углов между ними на основе формулы скалярного произведения двух нормальных векторов :

(7)

Из формулы (7) следует условие перпендикулярности прямых:

, или ,

а из формулы (6) – условие параллельности прямых:

или

Для определения расстояния от точки до прямой, заданной в общем виде, можно использовать формулу .

Задания:

1. Дано общее уравнение прямой . Написать:

а) уравнение с угловым коэффициентом; б) уравнение в отрезках на осях.

2. Написать уравнение прямой, проходящей через точку и составляющей с осью угол в .

3. Определить расстояние между прямыми

4. Написать уравнение перпендикуляра к прямой , проходящего через точку .

2. Плоскость.

Уравнение плоскости, проходящей через точку и перпендикулярной вектору , получается на основе использования скалярного произведения двух векторов. Пусть - произвольная точка плоскости . Тогда и по условию перпендикулярности векторов

(8)

Уравнение (8) называется уравнением плоскости, проходящей через заданную точку. После раскрытия скобок в данном уравнении получим общее уравнение плоскости в пространстве:

(9)

Угол, образованный двумя плоскостями, находится по формуле:

, где - нормальные векторы плоскостей + + .

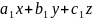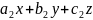Условие параллельности плоскостей имеет вид

Условием перпендикулярности плоскостей является равенство:

(10)

Расстояние от точки до плоскости определяется по формуле (11)

Задания:

1. Составить уравнение плоскости, проходящей через точку и перпендикулярной вектору

2. Написать уравнение плоскости, параллельной оси и проходящей через точки и

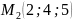
3. Составить уравнение плоскости, проходящей через точки и образующей угол с плоскостью

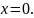
4. Найти расстояние от точки до плоскости

3. Прямая и плоскость в пространстве.

Прямая в пространстве может быть задана двумя пересекающимся плоскостями, уравнения которых + и + . Тогда уравнения прямой будут

(12)

Уравнения (12) называют общими уравнениями прямой.

Уравнения прямой , проходящей через точку и параллельной вектору , получаются на основе условия коллинеарности двух векторов и 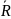: - каноническое уравнение прямой

Вектор называется направляющим вектором прямой.

Условие параллельности двух прямых имеет вид: , где и координаты направляющих векторов.

Условие перпендикулярности двух прямых записывается в виде:

.

Угол между прямой и плоскостью определяется выражением (13)

Условие параллельности прямой и плоскости имеет вид:

(14)

Условием перпендикулярности прямой и плоскости являются равенства:

(15)

Задания:

1. Написать уравнение прямой, проходящей через точки и 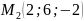и найти ее направляющие косинусы.

2. Показать, что прямая параллельна плоскости а прямая лежит в этой плоскости.

Индивидуальные задания