4.8 Расчет валов на совместное действие изгиба и кручение

Валы редуктора нагружены силами, действующими в зацеплениях передач, и испытывают деформации изгиба и кручения. Для упрощения расчётов принять, что силы являются сосредоточенными, приложены в серединах венцов зубчатых колёс и направлены по нормалям к профилям зубьев в полюсах зацепления. При расчёте их раскладывают на составляющие, действующие вдоль координатных осей. Схема редуктора и усилий, действующих в передачах, приведена на рисунке 12.

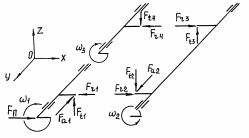
Рисунок 12- Схема редуктора и усилий, действующих в передачах

Окружные усилия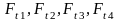 , Н, действующие в передачах, находим по формулам:

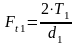, (4.83)

,

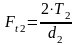, (4.84)

,

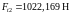(4.85)

,

, (4.86)

.

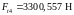Радиальные усилия 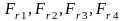, Н, действующие в передачах, находим по формулам:

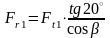, (4.87)

,

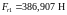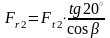, (4.88)

,

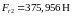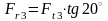, (4.89)

,

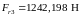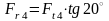, (4.90)

.

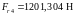Осевые усилия 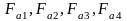, Н, действующие в передачах, находим по формулам:

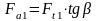, (4.91)

,

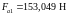, (4.92)

,

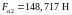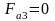, (4.93)

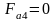. (4.94)

Последовательность расчета рассмотрим на примере промежуточного вала, подвергающегося действию наибольшего числа зуба.

Реакции в опорах вала (подшипниках) от сил, действующих в плоскости XOZвдоль оси Z (см. рисунок 13):

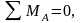
, (4.95)

,

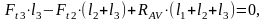
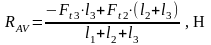(4.96)

.

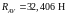Реакции в опорах вала от сил, действующих в плоскости XOY вдоль осей Xи Y:

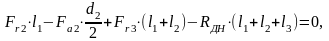
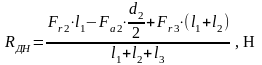, (4.97)

,

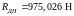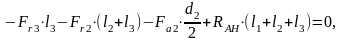
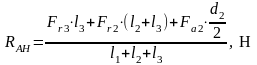, (4.98)

.

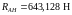Суммарные реакции:

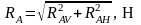, (4.99)

,

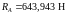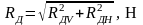, (4.100)

.

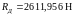Изгибающие моменты и эпюры участка вала АВ, обусловленные силами, действующими в плоскости XOZ:

, (4.101)

,

.

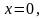
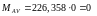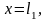
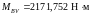Изгибающие моменты и эпюры участка вала ВС, обусловленные силами, действующими в плоскости XOZ:

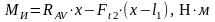, (4.102)

,

.

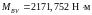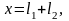
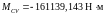Изгибающие моменты и эпюры участка вала СД, обусловленные силами, действующими в плоскости XOZ:

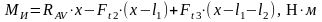, (4.103)

,

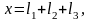
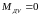
Изгибающие моменты и эпюры участка вала АВ, обусловленные силами, действующими в плоскости XOY:

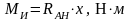, (4.104)

,

.

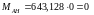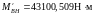Изгибающие моменты и эпюры участка вала ВС, обусловленные силами, действующими в плоскости XOY:

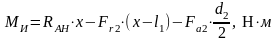, (4.105)

,

.

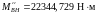Изгибающие моменты и эпюры участка вала СД, обусловленные силами, действующими в плоскости XOY:

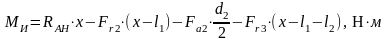(4.106)

,

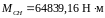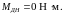
По найденным значениям изгибающих моментов строятся эпюры (см. рисунок 13).

Рисунок 13 – Эпюры изгибающих моментов

Суммарные изгибающие моменты:

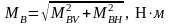, (4.107)

,

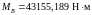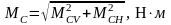, (4.108)

.

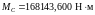Эквивалентный момент по третьей теории прочности ( ):

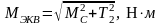, (4.109)

.

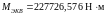Диаметр вала в опасном сечении , мм, находим по формуле:

(4.110)

Допускаемое напряжение [_и] выбирают невысоким, чтобы валы имели достаточную жесткость, обеспечивающую нормальную работу зацепления и подшипников. Валы рекомендуется изготавливать изсталей35, 40, 45,Ст 5, Ст 6, для которых 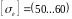МПа.

Вычисленные значения диаметра вала d в опасном сечении сравниваем с диаметром d_к под колесом, найденным при ориентировочном расчете . Должно выполняться условие: 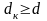. При невыполнении этого условия следует принять 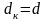и вновь определить размеры вала .

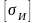– выбираем равным 55 МПа

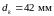
Вывод: условие выполняется.

4.8.1 Расчет вала на сопротивление усталости

Расчет вала на сопротивление усталости заключается в определении действительного коэффициента запаса прочности для сечения, имеющего

наибольший изгибающий момент, и в сопоставлении его с допускаемым.

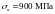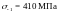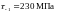Сталь 45, 270 HB, ее механические характеристики, такие, как: временное сопротивление , среднее напряжение цикла и , пределы выносливости гладких образцов при симметричном цикле изгиба и кручения и , коэффициент чувствительности к асимметрии цикла нагружения .

Момент сопротивления W₁, мм³ при изгибе вычисляем по формуле:

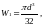(4.111)

где d – диаметр проверяемого участка вала, мм,

_{Напряжение в опасном сечении, МПа:}

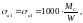(4.112)

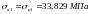
Момент сопротивления W_К1, мм³ при кручении вычисляем по формуле:

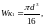(4.113)

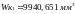
_{Крутящий момент, Нм:}

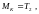(4.114)

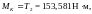
_{Амплитуда касательных напряжений цикла, МПа:}

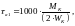(4.115)

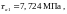
_{Среднее напряжение цикла, МПа:}

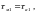(4.116)

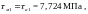
_{Зубчатое колесо установлено на валу с натягом. Поэтому концентратор напряжений в сечении – посадка с натягом. Посадочную поверхность вала под зубчатое колесо шлифуют (Ra = 0,8 мкм); коэффициенты влияния качества поверхност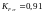и и 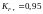. Поверхность вала – без упрочнения: , где Кv – коэффициент влияния поверхностного уплотнения. Эффективные коэффициенты концентрации напряжений и 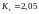. Коэффициенты касательного и нормального напряженного состояния соответственно 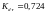и .}

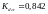_{Коэффициенты снижения предела выносливости и :}

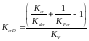(4.117)

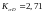
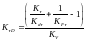(4.118)

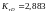
_{Пределы выносливости вала и :}

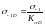(4.119)

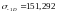
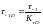(4.120)

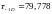
_{Коэффициент чувствительности к асимметрии цикла касательного напряжения:}

(4.121)

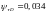
_{Коэффициент запаса по нормальному напряжению:}

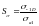(4.122)

_{Коэффициент запаса по касательному напряжению:}

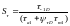(4.123)

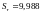
_{Коэффициент запаса прочности:}

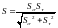(4.124)