
- •Методические указанИя
- •Тема 1. “Решение прямоугольных треугольников” Краткие теоретические сведения
- •Образец решения задач
- •Тема 2. “Решение косоугольных треугольников” Краткие теоретические сведения
- •Образец решения задач
- •Тема 3. “Прикладные задачи, связанные с решением прямоугольных и косоугольных треугольников”
- •Тема 4. “Вычисление площадей поверхностей и объёмов сооружений”
- •Тема:5. “Множества и графы” Краткие теоретические сведения
- •Образец решения задач
- •Тема6. “Элементы математической статистики” Краткие теоретические сведения
- •Функция распределения случайной величины
- •Функция распределения дискретной случайной величины
- •Образец решения задач
- •Тема7. “Классическое определение вероятности” Краткие теоретические сведения
- •Образец решения задач
Образец решения задач
Даны множества:
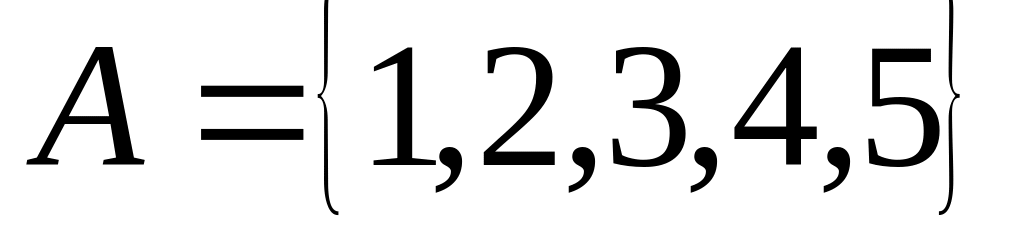
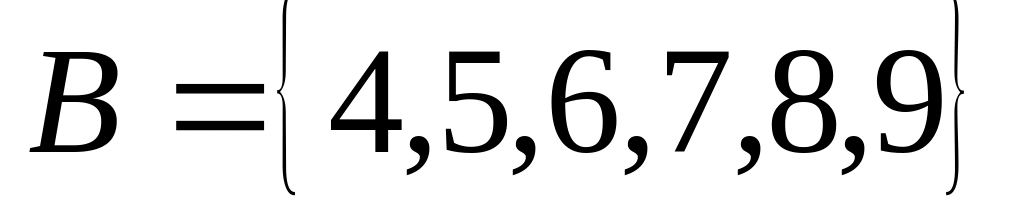
Найти:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Решение
![]()
![]()
![]()
![]()
Даны множества:
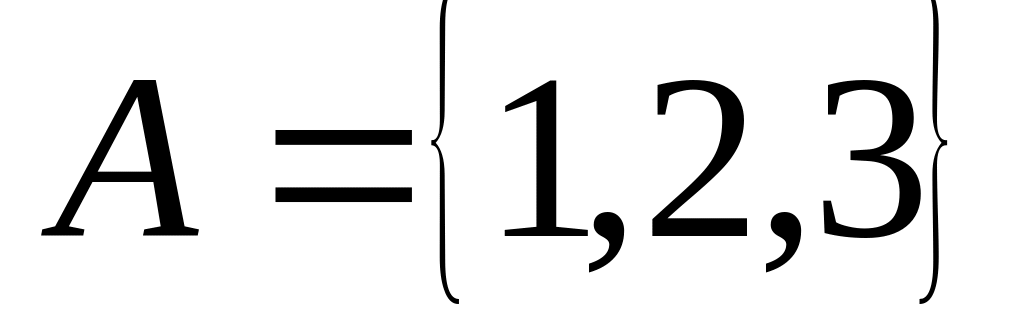 ,
,
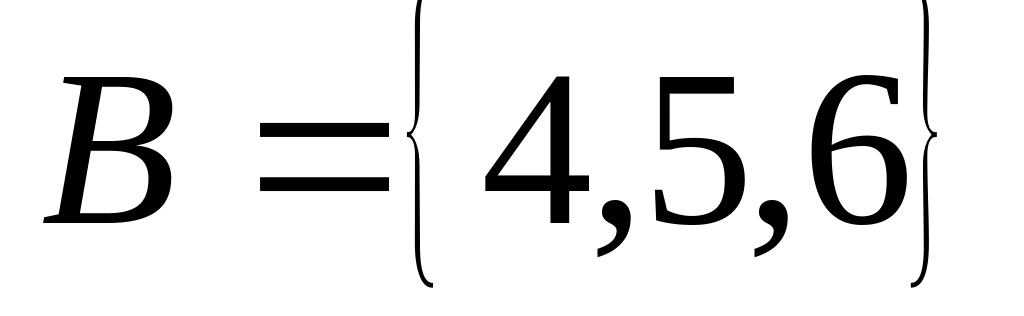 ,
,
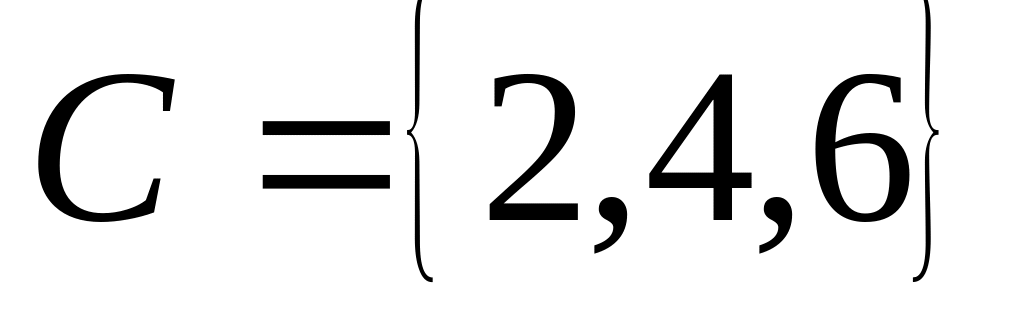
Найти:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Решение
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Даны множества: ,
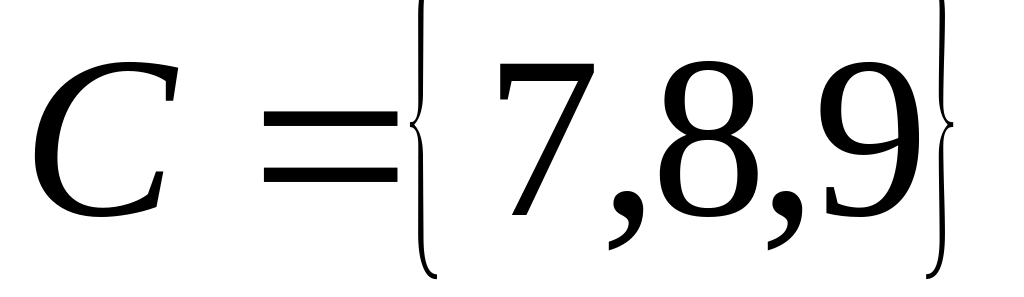 ,
,
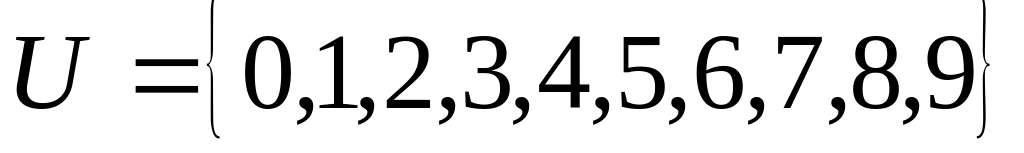
Найти:
![]() ,
,
![]()
Построить диаграммы Эйлера-Венна.
Решение
![]()
![]()
Построить диаграмму Эйлера-Венна.

![]()
![]()
![]()
![]()
Построить диаграмму Эйлера-Венна.

Найти Гамильтонов путь от вершены 1 к вершине 5

Решение

Ответ. 1, 4, 5 или 1, 3, 5
Тема6. “Элементы математической статистики” Краткие теоретические сведения
Математическая статистика – это наука, изучающая случайные явления посредством
обработки и анализа результатов наблюдений и измерений.
Первая задача математической статистики – указать способы получения, группировки и обработки статистических данных, собранных в результате наблюдений, специально поставленных опытов или произведённых измерений.
Вторая задача математической статистики – разработка методов анализа статистических сведений в зависимости от целей исследования.
Случайную величину
 будем
называть генеральной
совокупностью
.
будем
называть генеральной
совокупностью
.
Исходным
материалом для изучения свойств
генеральной совокупности
являются
статистические данные, т.е. значения
,
полученные в результате повторения
случайного опыта (измерения случайной
величины
).
Предполагается, что опыт может быть
повторён сколько угодно раз в неизменных
условиях. Это означает, что распределение
случайной величины ![]() ,
, ![]() ,
заданной на множестве исходов
,
заданной на множестве исходов ![]() -го
опыта, не зависит от
и
совпадает с распределением генеральной
совокупности
.
-го
опыта, не зависит от
и
совпадает с распределением генеральной
совокупности
.
Набор ![]() независимых
в совокупности случайных величин
независимых
в совокупности случайных величин ![]() ,
где
соответствует
-му опыту,
называют случайной
выборкой из
генеральной совокупности
.
Число
называется объёмом
выборки.
,
где
соответствует
-му опыту,
называют случайной
выборкой из
генеральной совокупности
.
Число
называется объёмом
выборки.
Совокупность
чисел ![]() ,
полученных в результате
-кратного
повторения опыта по измерению генеральной
совокупности
,
называется выборкой
объёма
.
,
полученных в результате
-кратного
повторения опыта по измерению генеральной
совокупности
,
называется выборкой
объёма
.
В основе большинства результатов математической статистики лежит выборочный метод, состоящий в том, что свойства генеральной совокупности устанавливаются путём изучения тех же свойств на случайной выборке.
Прежде, чем перейти к детальному анализу статистических данных, обычно проводят их предварительную обработку. Иногда её результаты уже сами по себе дают ответы на многие вопросы, но в большинстве случаев они являются исходным материалом для дальнейшего анализа.
Простейшее преобразование статистических данных является их упорядочивание по
величине.
Выборка
объёма
из
генеральной совокупности
,
упорядоченная в порядке не
убывания элементов,
т.е. ![]() ,
называется вариационным
рядом:
,
называется вариационным
рядом:
![]() .
.
Разность
между максимальным и минимальным
элементами выборки ![]() называют размахом
выборки.
называют размахом
выборки.
Пусть выборка содержит
 различных
чисел
различных
чисел  ,
где
,
где 
и ![]() ,
причём число
,
причём число ![]() встречается
в выборке
встречается
в выборке ![]() раз,
раз, ![]() .
Так бывает либо тогда, когда генеральная
совокупность
-
дискретная случайная величина, либо
когда
-
непрерывна, но её значения при измерении
округляют.
.
Так бывает либо тогда, когда генеральная
совокупность
-
дискретная случайная величина, либо
когда
-
непрерывна, но её значения при измерении
округляют.
Число
называют частотой элемента
выборки
,
а отношение ![]() - относительной
частотой этого
элемента.
- относительной
частотой этого
элемента.
Статистическим рядом для данной выборки называют таблицу, которая в первой строке содержит значения выборки (напомним: ), во второй строке – частоты , а в третьей строке – относительные частоты этих значений:
Значения |
|
|
… |
|
Частоты |
|
|
… |
|
Относительные частоты
|
|
|
… |
|
Статистические данные, представленные в виде статистического ряда, называют группированными.
По данным дискретного вариационного ряда строят полигон частот или относительных
частот или гистограмму.
Полигоном частот называют ломанную, отрезки которой соединяют точки (x1; n1), (x2; n2), ..., (xk; nk). Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат - соответствующие им частоты ni. Точки ( xi; ni) соединяют отрезками прямых и получают полигон частот (рис. 1).
Полигоном относительных частот называют ломанную, отрезки которой соединяют точки (x1; W1), (x2; W2), ..., (xk; Wk). Для построения полигона относительных частот на оси абсцисс откладывают варианты xi, а на оси ординат - соответствующие им относительные частоты Wi. Точки ( xi; Wi) соединяют отрезками прямых и получают полигон относительных частот.
В случае непрерывного признака целесообразно строить гистограмму.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению ni / h (плотность частоты).
Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии ni / h.
Площадь i - го частичного прямоугольника равна hni / h = ni - сумме частот вариант i - го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению Wi / h (плотность относительной частоты).
Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии Wi / h (рис. 2).
Площадь i - го частичного прямоугольника равна hWi / h = Wi - относительной частоте вариант попавших в i - й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.
Рис. 1. Полигон частот |
Рис. 2. Гистограмма относительных частот |
Наиболее важными характеристиками случайной величины являются математическое ожидание, дисперсия и среднее квадратическое отклонение.
Математическим ожиданием дискретной случайной величины называют сумму
произведений всех её возможных значений на их вероятности.
![]() или
или
![]()
Математическое ожидание приближённо равно среднему значению случайной величины.
Дисперсией дискретной случайной величины называют математическое ожидание квадрата
отклонения случайной величины от её математического ожидания.
Отклонением называют разность между случайной величиной и её математическим ожиданием.
Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом её математического ожидания.
![]() или
или
![]()
Средним квадратическим отклонением случайной величины Х называют квадратный
корень из дисперсии.
![]()
Кроме степенных средних в статистике для относительной характеристики величины пользуются структурными средними: модой и медианой.
Мода — это наиболее часто встречающийся вариант ряда. Мода применяется, например,
при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного ряда является варианта, обладающая наибольшей частотой.
Медиана — это значение признака, которое лежит в основе ранжированного ряда и делит
этот ряд на две
равные по численности части. Для
определения медианы в
дискретном ряду при
наличии частот сначала вычисляют
полусумму частот ![]() ,
а затем определяют, какое значение
варианта приходится на нее. (Если
отсортированный ряд содержит нечетное
число признаков, то номер медианы
вычисляют по формуле: Ме =
(n(число
признаков в совокупности) +
1)/2, в случае
четного числа признаков медиана будет
равна средней из двух признаков
находящихся в середине ряда).
,
а затем определяют, какое значение
варианта приходится на нее. (Если
отсортированный ряд содержит нечетное
число признаков, то номер медианы
вычисляют по формуле: Ме =
(n(число
признаков в совокупности) +
1)/2, в случае
четного числа признаков медиана будет
равна средней из двух признаков
находящихся в середине ряда).
Из всех показателей вариации стандартное отклонение в наибольшей степени используется
для проведения статистического анализа. Однако среднеквадратическое отклонение дает абсолютную оценку меры разбросанности значений и чтобы понять, насколько она велика относительно самих значений, требуется относительный показатель. Такой показатель существует и называется он коэффициент вариации. Формула коэффициента вариации очень проста:
![]()
Как видно, это отношение стандартного отклонения к средней величине. Данный показатель
измеряется в процентах (если умножить на 100%). Имея коэффициенты вариации, можно сравнивать однородность самых разных явлений независимо от их масштаба и единиц измерения.
В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной.


