
Рекомендуемая литература
1.Дмитриева В.Ф. Физика для профессий и специальностей технического профиля. Сборник задач: учеб.пособие для студ. учреждений сред. проф. образования / В.Ф. Дмитриева. – 4ё–е изд., стер. – М.: Издательский центр «Академия», 2014. – 256 с.
2.Дмитриева В.Ф. Физика для профессий и специальностей технического профиля. Контрольные материалы: учеб.пособие для студ. учреждений сред. проф. образования/ В.Ф. Дмитриева, Л. И. Васильев. – 3–е изд., стер. – М.: Издательский центр «Академия», 2014. – 112 с.
Практическое занятие №2
Тема: Кинематика и динамика вращательного движения твердого тела. Законы сохранения.
Цель: обобщение и систематизация знаний, умений по данной теме; формирование практических навыков в решении задач; развитие интереса к изучению физики
Краткие теоретические сведения
Таблица 2.1 – Основные законы и формулы
Физические законы, формулы, переменные |
Формулы |
Ускорение при криволинейном движении: 1) нормальное где R – радиус кривизны траектории, 2) тангенциальное,3) вектор полного ускорения,4) модуль полного ускорения. |
1) 3)
|
1)
угловое перемещение
2)
угловая скорость
где dt – интервал времени. 3)
угловое ускорение
Единицы измерения:
|
2) 3) |
Равномерное вращение: 1) период вращения Т: 2) частота вращения ν: Единицы измерения:
|
1)
2) |
Равноускоренное вращение β=const: 1) уравнение углового перемещения где ω0 – начальная угловая скорость 2)уравнение угловой скорости: где R – радиус – расстояние от центра вращения до материальной точки; 3) нормальное ускорение: 4) тангенциальное ускорение: 5)полное ускорение: |
1) 2) 3) 4) 5) |
Связь линейной υ и угловой скорости ω: |
|
1)Момент инерции J материальной точки относительно оси вращения: где mi– масса точки, ri – расстояние от оси вращения до материальной точки; 2) Момент инерции системы (тела) относительно оси вращения:1
|
1) 2) |
Теорема Штейнера: где JZ– момент инерции относительно произвольной оси Z, JC– момент инерции относительно параллельной оси, проходящей через центр масс С, а – расстояние между осями. |
|
1)Кинетическая энергия вращения ЕВР: где JZ - момент инерции тела относительно произвольной оси Z; ω – угловая скорость материальных точек тела. 2)Полная кинетическая энергия тела: ЕК – кинетическая энергия поступательного движения тела, m– масса тела, υ –скорость тела. |
1) 2) |
1)
Момент силы где
– радиус
– вектор, проведенный в точку приложения
силы
2) Модуль момента силы: где α – угол между векторами и , l – плечо силы.
|
1)
2) |
Основное уравнение динами вращательного движения твердого тела: где – момент силы, J – главный момент инерции тела( момент инерции относительно главной оси), – угловое ускорение. |
|
|
1)
2)
|
1)Момент
импульса материальной точки
где
– радиус
– вектор,
2) Момент импульса твердого телаотносительно оси Z: где
mi
– масса отдельной части твердого
тела, υi
–скорость частицы,
3) Закон сохранения момента импульса: |
1) 2) 3)
|
Работа силы F: где Fs – проекция силы на ось, направленную вдоль движения, S – модуль перемещения, α - угол между вектором силы и направлением перемещения
|
|
Мощность N: dA
– элементарная работа, dt
– интервал времени,
– вектор силы,
|
|
Кинетическая энергия К: m
– масса тела; υ – скорость.
|
|
Потенциальная энергия П:
|
1)
2)
|
Закон сохранения энергии: |
|
КПД (коэффициент полезного действия): где Апол - полезная работа, Азат - затраченная работа. |
|

 ,2)
,2) ,
, ,4)
,4)

 .
. :
: :
: ;
;
 ;
;
 .
. ;
; .
. ;
;

 ;
; .
. ;
;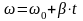 ;
; ;
;
 .
. ,
,
 ;
; .
.
 ;
; .
. :
: ;
;
 ;
; .
.
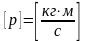
 ;
;
 :
: - импульс точки, m
– масса,
–скорость
точки,
- импульс точки, m
– масса,
–скорость
точки, – радиус
– вектор, ω – угловая скорость, JZ
- момент инерции тела относительно
произвольной оси Z,
– радиус
– вектор, ω – угловая скорость, JZ
- момент инерции тела относительно
произвольной оси Z,
 ,
, ,
,


 - перемещение,
- скорость тела.
- перемещение,
- скорость тела.




 ;
;

