12. Формула для вычисления обратной матрицы.

Алгоритм нахождения обратной матрицы

Найти определитель исходной матрицы. Если определитель равен 0, то матрица А – вырожденная и обратной матрицы не существует.

Если определитель не равен нулю, то находим транспонированную матрицу ( ).

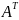Составить присоединенную матрицу . Найти алгебраическое дополнение элементов транспонированной матрицы и составить из них присоединенную матрицу.

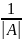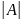Вычислить обратную матрицу: = * , где - определитель исходной матрицы

Проверить правильность вычислений, исходя из определения: * А = А * = Е

13. Основные свойства обратной матрицы.

• ( = *

• 

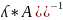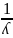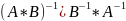
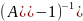• =А

• = =

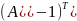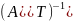14. Ранг матрицы

В матрице размера вычеркиванием каких либо строк и столбцов можно выделить квадратные подматрицы 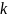- ого порядка, где

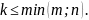
Определителем таких подматриц называется минорами – ого порядка матрицы А.

Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы. Обозначается rand A или r (А).

Из определения следует:

• Ранг матрицы размера не превосходит меньшего из ее размеров, то есть r (А)

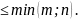
• r (А) = 0 только тогда, когда все элементы матрицы равны 0, то есть А = 0

• Для квадратной матрицы n – ого порядка r (А)=n, тогда и только тогда, когда матрица А – невырожденная

Определение ранга матрицы перебором всех миноров достаточно трудно. Для облегчения используются элементарные преобразования, сохраняющие ранг матрицы:

• Отбрасывание нулевой строки (столбца).

• Умножение всех элементов строки (столбца) матрицы на число, не равное нулю.

• Изменение порядка строк (столбцов).

• Прибавление к данному элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.

• Транспонирование матрицы.

Теор:

• Ранг матрицы не изменится при элементарных преобразованиях матрицы.

• Ранг ступенчатой матрицы равен r, т.к. имеется минор r –ого порядка не равный 0.

15. Теорема Кронекера - Капели

Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.

16. Решение систем линейных уравнений методом Гаусса

Метод гаусса- это метод последовательного исключения переменных; заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого или треугольного вида.

17. Формула Крамера

Метод Крамера (для квадратной матрицы n x n) - Пусть - определитель м-цы А, а ₁ получен из матрицы с заменой j-го столбца столбцом свободных членов. Тогда, если ≠ 0, то система имеет ед. решение, определенное по формуле Крамера: x_j= _j / (j=1…n)

18. Фундаментальная система решений (ФСР) однородной системы линейных уравнений.

Называется n − r линейно независимых решений этой системы (или базис ядра оператора)

Теорема о ФСР: пусть ранг основной м-цы, r(A) меньше, чем n (r<n), где n – число переменных, тогда

1. ФСР существует, y₁, y₂, y_k, состоит из k векторов (k=n-r)

2. Общее решение системы имеет вид: Х_общ=c₁y₁+c₂y₂+…+c_n-ry_n-r

3. Если n=r, то ФСР не существует