Список вопросов по Линейной Алгебре

1. Матрицы. Основные операции над матрицами.

Матрица – это производная таблица чисел.

Две матрицы А и В одного и того же размера m*n называются равными, если они совпадают поэлементно, т.е. .

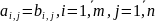Основные операции над матрицами.

• Умножение матрицы на число. Произведение матрицы А на число ƛ называется матрица В (В=ƛ*А), элементы которой вычисляются как ,

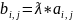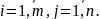
• Суммой двух матриц А и В одинакового размера m*n называется матрица С=А+В, элементы которой .

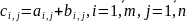• Разность двух матриц одинакового размера определяется через предыдущие операции, т.е. А-В=А+(-В)

• Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц называется такая матрица С, каждый элемент которой 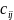равен сумме произведений элементов i-строки матрицы А на j-столбец матрицы В.

2. Квадратная матрица. Диагональная и единичная матрицы. Примеры

Классификация матриц.

1. Матрица, состоящая из одной строки/столбца, называется вектор-строка/вектор-столбец. ;

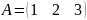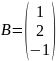
2. Кв. матрицей n-го порядка наз-ся матрица, у которой число строк равняется числу столбцов.

3. Элементы матрицы 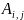, у которой i=j, называется диагональными. Они образуют главную диагональ.

4. Если все недиагональные эл-ты матрицы равны нулю, то она называется диагональной.

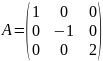
5. Единичной называется диагональная матрица, элементы которой равны 1.

6. Симметричной называется квадратная матрица, у которой элементы, расположенные симметрично относительно главной диагонали, равны.

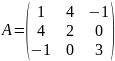
7. Треугольная матрица – это кв. матрица, у которой все эл-ты, стоящие по одну из сторон главной диагонали равны 0.

3. Транспонированная матрица. Пример.

Транспонирование матрицы – это переход от матрицы A к , в которой строки и столбцы поменялись местами с сохранением порядка.

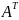называется транспонированной относительно матрицы А.

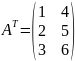
4. Элементарные строчечные преобразования. Эквивалентные матрицы.

• перестановка местами любых двух строк матрицы;

• умножение любой строки матрицы на константу k, k

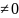
• прибавление к любой строке матрицы другой строки.

Аналогично определяются элементарные преобразования столбцов.

Элементарные преобразования обратимы.

Если от матрицы A к матрице B перешли с помощью эквивалентных преобразований над строками, то такие матрицы называются эквивалентными и обозначают .

5. Выражение определителя непосредственно через его элементы (для кв. Матриц размера 2*2 и 3*3)

Каждой квадратной матрице А можно поставить в соответствие вычисленное по определенным правилам число, называемое определителем кв. матрицы.

Определителем матрицы второго порядка или определителем второго порядка называется число, которое вычисляется по формуле

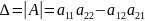
Определителем матрицы третьего порядка или определителем третьего порядка называется число, которое вычисляется по формуле: