
- •Контрольные задания и методические рекомендации для студентов заочного обучения Севастополь 2013 г.
- •I семестр
- •Модуль 1 Линейная алгебра. Векторная алгебра Задачи для решения.
- •Решение типовых задач Задание 1
- •Задание 2
- •Модуль 2
- •Задачи для решения
- •Решение типовых задач
- •Задачи для решения
- •Определение предела функции
- •Непрерывность функции
- •II семестр
- •Повторное дифференцирование.
- •Модуль 4
- •Задачи для решения Задание 1
- •Решение типовых задач Задание 1
- •Задание 2
- •Задание 3
- •Задачи для решения Задание 1
- •Задание 3
- •Решение типовых задач
- •Задачи для решения
- •Задание 2
- •Задание 3
- •Решение типовых задач
- •Задание 2
- •III семестр
- •Задачи для решения
- •Варианты
- •Варианты
- •Варианты
- •Решение типовых задач
- •Дифференциальные уравнения первого порядка
- •Дифференциальные уравнения высших порядков Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Задачи для решения
- •Варианты
- •Решение типовых задач
- •Решение типовых задач
- •Числовые ряды
- •Обобщенно-гармонический ряд:
- •Ряды Фурье
- •IV семестр
- •Модуль 9 Операционное исчисление Задачи для решения
- •Решение типовых задач
- •Свойства преобразования Лапласа
- •Теория вероятностей Задачи для решения
- •Решение типовых задач
- •Сведения из теории
- •Нормальный (гауссовский) закон распределения. Кривая нормального распределения.
- •Литература
Задачи для решения Задание 1
Непосредственным интегрированием найти следующие интегралы:
Вариант № 1 Вариант № 2
1.![]() ;
1.
;
1.![]() ;
;
2.![]() ;
2.
;
2.![]() ;
;
3.![]() ;
3.
;
3.
![]() ;
;
4.![]() . 4.
. 4.![]() .
.
Вариант № 3 Вариант № 4
1.![]() ;
1.
;
1.![]() ;
;
2.![]() ; 2.
; 2.![]() ;
;
3.![]() ;
3.
;
3.![]() ;
;
4.![]() . 4.
. 4.![]() .
.
Вариант № 5 Вариант № 6
1.![]() ;
1.
;
1.![]() ;
;
2.![]() ;
2.
;
2.![]() ;
;
3.![]() ;
3.
;
3.![]() ;
;
4.![]() . 4.
. 4.![]() .
.
Вариант № 7 Вариант № 8
1.![]() ;
1.
;
1.![]()
2.![]() ;
2.
;
2.![]()
3.![]() ;
3.
;
3.![]()
4.![]() . 4.
. 4.![]() .
.
Вариант № 9 Вариант № 10
1.![]() ; 1.
; 1.![]() ;
;
2.![]() ;
2.
;
2.![]() ;
;
3.![]() ;
3.
;
3.![]() ;
;
4.![]() ;
4.
;
4.![]() .
.
Задание 2
Проинтегрировать, выбрав нужный метод интегрирования.
Вариант № 1 Вариант № 2
1.![]() ;
1.
;
1.![]() ;
;
2.![]() ;
2.
;
2.![]() ;
;
3.![]() ;
3.
;
3.![]() ;
;
4.![]() .
4.
.
4.![]() .
.
Вариант № 3 Вариант № 4
1.![]() ;
1.
;
1.![]() ;
;
2.![]() ;
2.
;
2.![]() ;
;
3.![]() ;
3.
;
3.![]() ;
;
4.![]() .
4.
.
4.![]() .
.
Вариант № 5 Вариант № 6
1.![]() ; 1.
; 1.![]() ;
;
2.
![]() ;
2.
;
2.![]() ;
;
3.
![]() ;
3.
;
3.![]() ;
;
4.![]() .
4.
.
.
4.
.
Вариант № 7 Вариант № 8
1.![]() ;
1.
;
1.![]() ;
;
2.![]() ; 2.
; 2.![]() ;
;
3.![]() ;
3.
;
3.![]() ;
;
4.![]() .
4.
.
4.![]() .
.
Вариант № 9 Вариант № 10
1.
![]() ;
1.
;
1.
![]() ;
;
2.![]() ;
2.
;
2.
![]() ;
;
3.![]() ;
3.
;
3.![]() ;
;
4.![]() .
4.
.
4.![]() .
.
Задание 3
Вычислить определённый интеграл.
Варианты
1.
![]() ;
2.
;
2.
 ;
3.
;
3.![]() 4.
4.![]()
5.
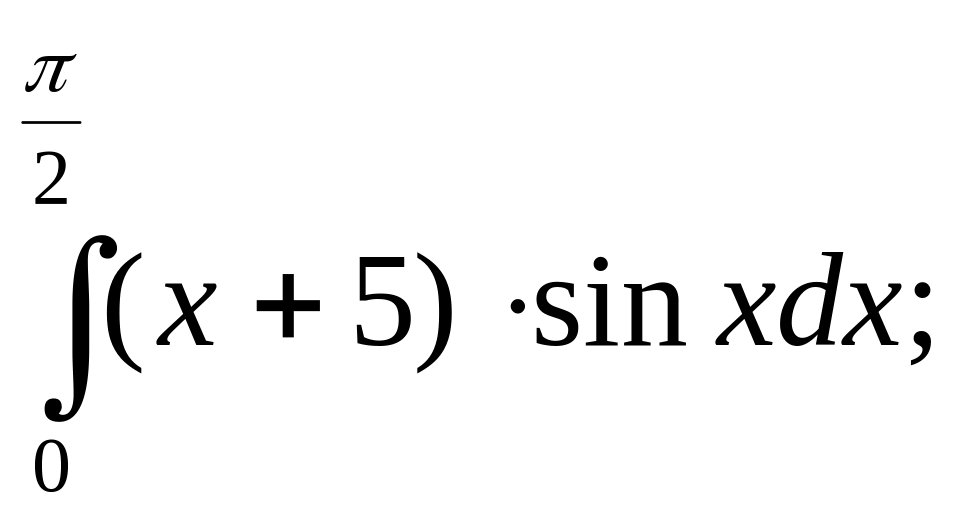 6.
6.![]() 7.
7.
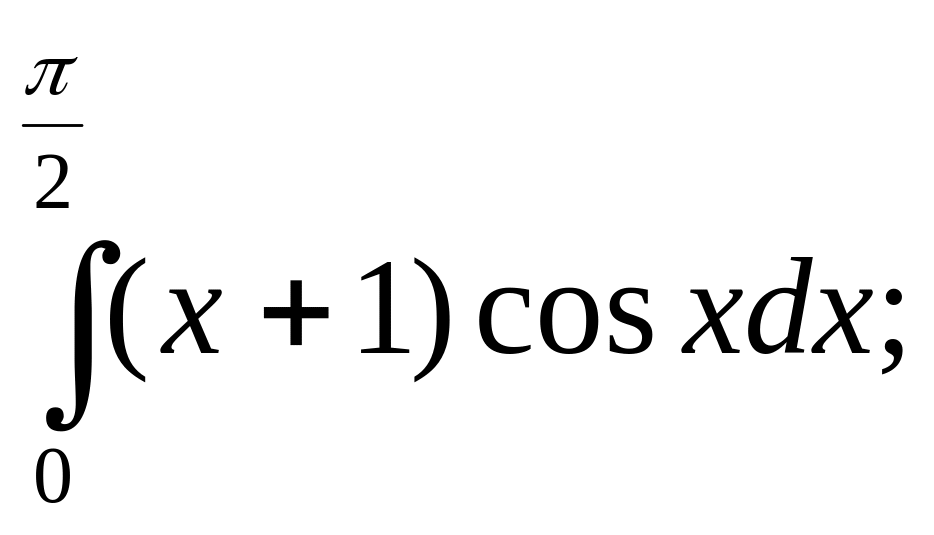 8.
8.
![]() 9.
9.
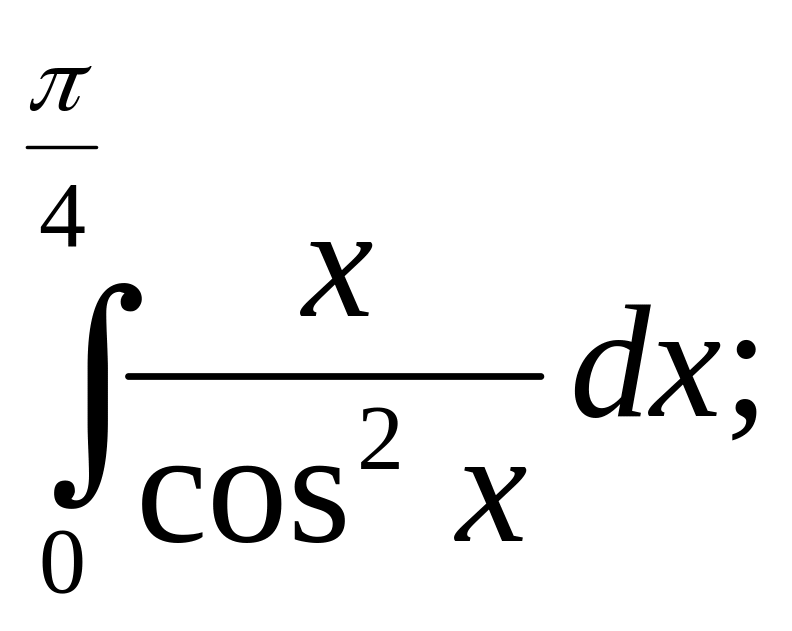 10.
10.
![]()
Задание 4
Вычислить площадь фигуры, ограниченной данными линиями.
Варианты.
1. ху = 6, х + у = 7; 6. у = 2х – х2, у = 0;
2. у= 3х – х2, у = 0; 7. у = 6х – х2, у = 0;
3. ху = 8, х + у = 6; 8. у = 1 – х2, у = 0, х < 0;
4. у = 4х – х2, у = 0; 9. у = 9 – х2, х >0, у = 0;
5. у = 4 – х2, у = 0, х > 0; 10. у = 25 – х2, у = 0, х <0.
Задание 5
По формулам трапеций и парабол (Симпсона) приближенно вычислить интеграл.
Варианты
1.![]() ,
,
![]() ;
6.
;
6.![]() ,
,
![]() ;
;
2.![]() ,
;
7.
,
;
7.![]() ,
;
,
;
3.![]() ,
;
8.
,
;
8.![]() ,
;
,
;
4.![]() ,
;
9.
,
;
9.![]() ,
;
,
;
5.![]() ,
;
10.
,
;
10.![]() ,
.
,
.
