Определение предела функции
Число А называется пределом функции
y = f(x) при x стремящемуся
к а, если для любого сколь угодно
малого положительного числа эпсилон
(ε >0) найдется такое число δ (дельта),
величина которого зависит от ε (δ(ε) >
0), что при всех x ≠ a и удовлетворяющих
неравенству
выполняется неравенство |f(x)-A|
< ε. В этом случае пишут :
.
Если x →a и при этом x<a, то пишут х →a – 0.
Если x →a и при этом x >a, то пишут x → a+0.
Предел
называется левосторонним.
Предел
называется правосторонним.
Число А называется пределом функции
y = f(x) при х стремящемся
к ∞, если для любого малого положительного
числа ε (ε > 0) существует такое
положительное число М, величина которого
зависит от ε (М(ε) > 0), что для всех
значений х, удовлетворяющих
неравенству |x| > М(ε), будет выполняться
неравенство |f(x)-A| < ε. В этом случае
пишут
.
При вычислении пределов функций необходимо знать следующие теоремы:
1.
,
где С – постоянная.
2.
,
где С – постоянная.
3. Если
и
существуют, то
.
4.
.
5.
,
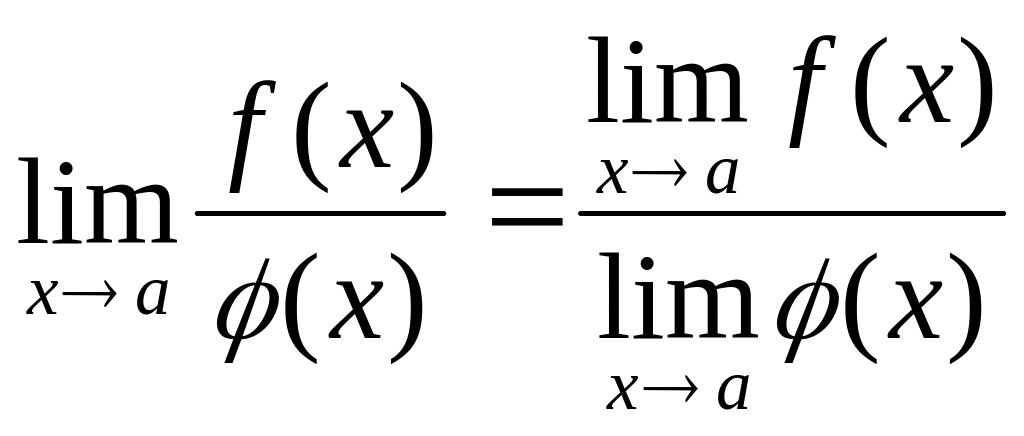если
≠
0.
Они справедливы как для пределов числовых последовательностей, так и для пределов функций. Перечисленные свойства справедливы как для x→a, так и для x→ ∞.
Два замечательных предела.
Первым
замечательным пределом называют
предел
.
Его используют
для раскрытия неопределённостей вида
.
Вторым замечательным пределом называют предел
или
.
Его используют
для раскрытия неопределённостей вида
.
Пример выполнения задания 1
а) .
В данном случае
имеем неопределенность [
].
Для раскрытия неопределенности разделим
числитель и знаменатель на наибольшую
степень переменной, то есть, разделим
на x2.
.
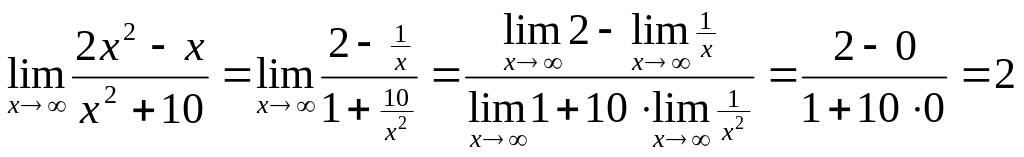б) .
При x→2
числитель и знаменатель дроби равны
нулю. Неопределенность вида [
].
Следовательно, необходимо данное
выражение преобразовать.
Числитель и знаменатель данной дроби при x = 2 обращается в ноль, поэтому многочлены x2- 5x + 6 и x2 - 2x делятся без остатка на бином (x – 2) (теорема Безу).
в) .
В данном случае имеем неопределенность вида [∞-∞].
Умножаем
выражение, стоящее под знаком предела,
на такой множитель, чтобы получить
разность квадратов:
.
Чтобы не нарушать тождество, на сопряжённый
множитель так же и разделим.
В результате получим:
.
П
ри
x→ + ∞ числитель и знаменатель дроби
– бесконечно большие величины, имеем
неопределенность вида [
].
Для раскрытия неопределенности разделим числитель и знаменатель на x2:
=
.
г) .
Предел основания равен 1, а показатель степени стремится к бесконечности. Имеем неопределенность вида [1∞].
Для вычисления предела преобразуем выражение так, чтобы выделить второй замечательный предел.
.
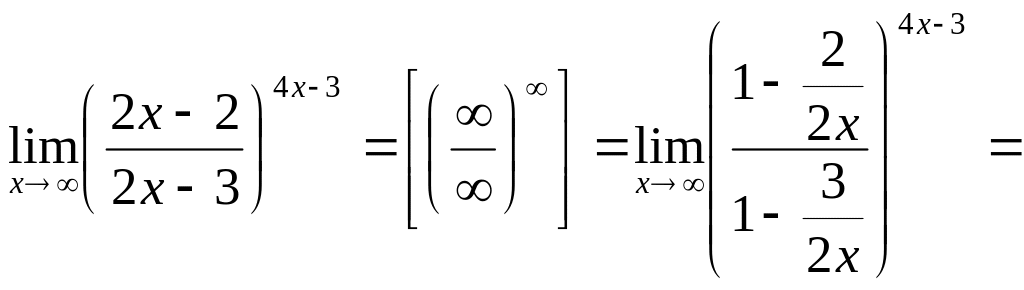
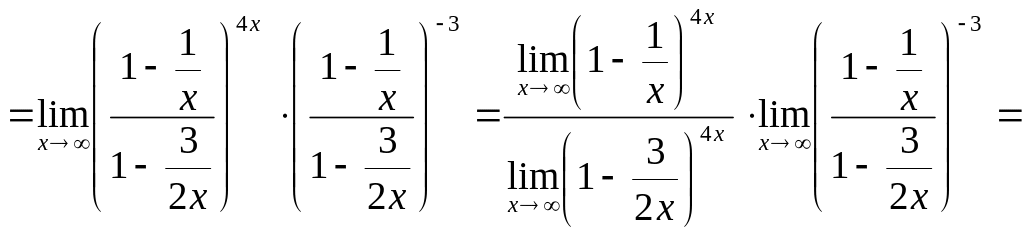
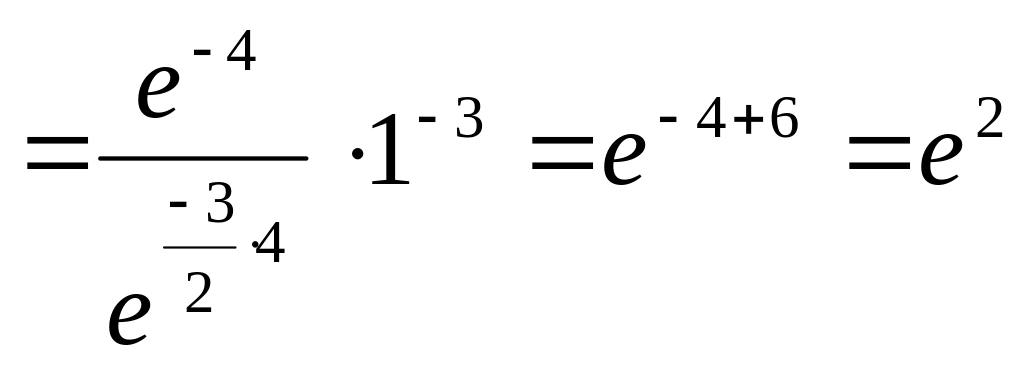д) .
В данном случае имеем неопределенность вида [ ].
Для вычисления предела преобразуем выражение так, чтобы выделить первый замечательный предел.
=
.
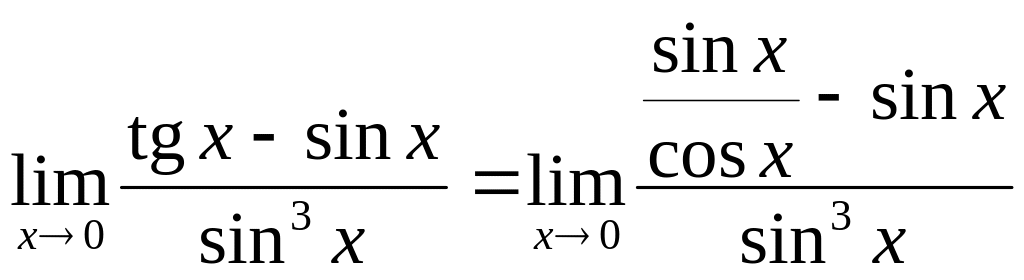
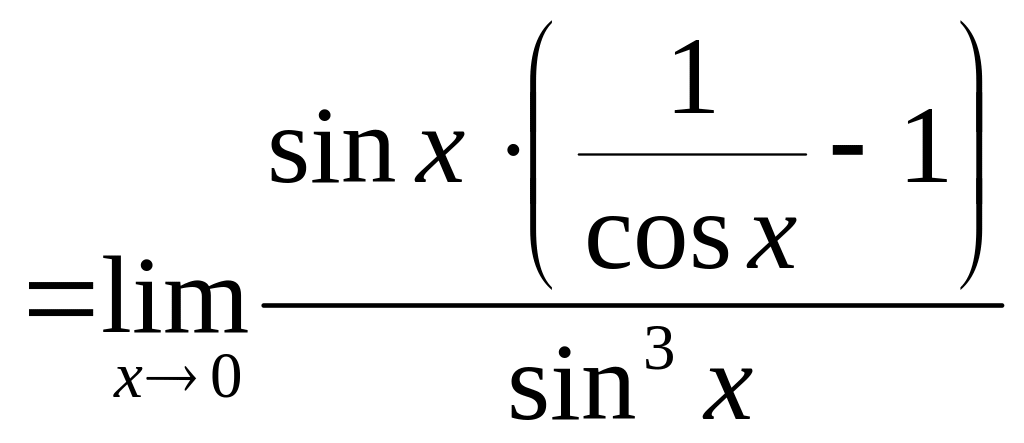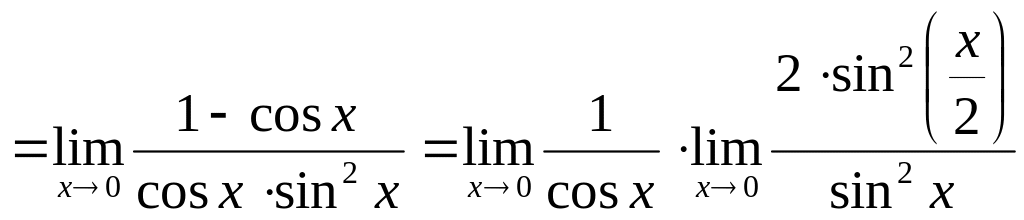Домножаем числитель и знаменатель дроби на х2:
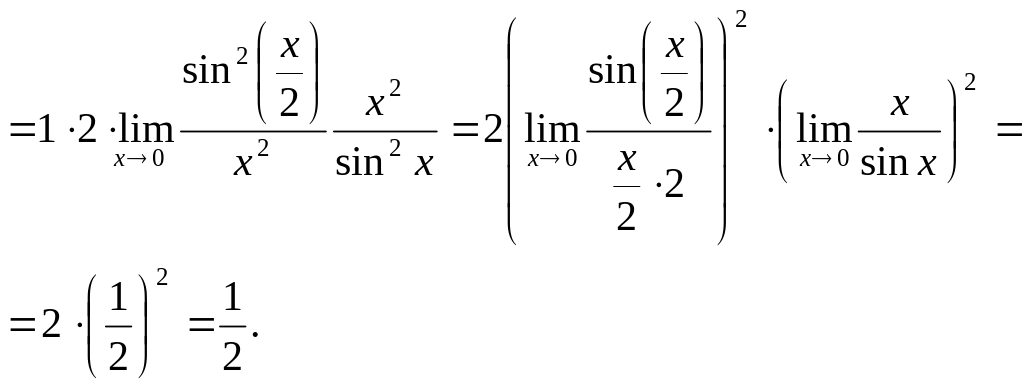
Сведения из теории
Непрерывность функции
Функция y = f(x) называется непрерывной в точке х = а, если
функция определена в этой точке и ее окрестности;
существует
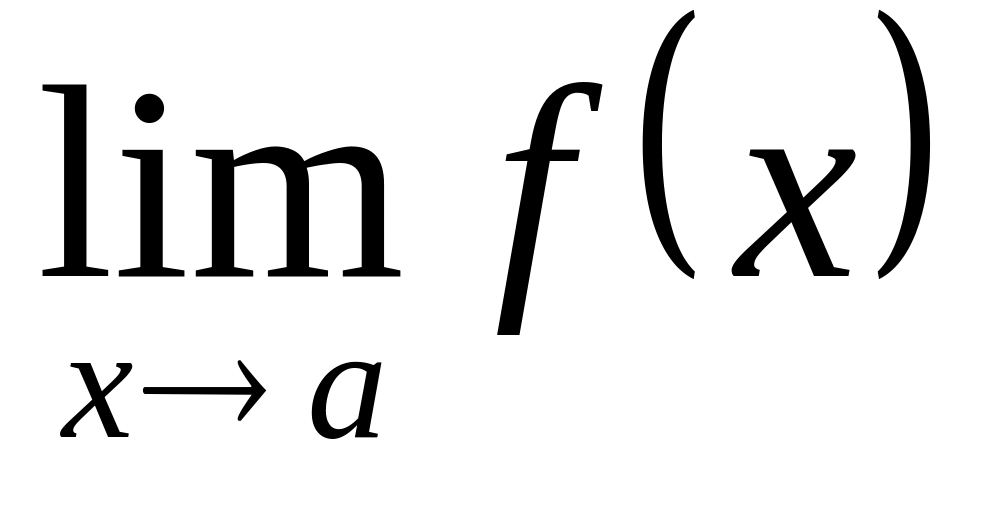;предел фнкии равен значению функции в точке а, т.е.
.
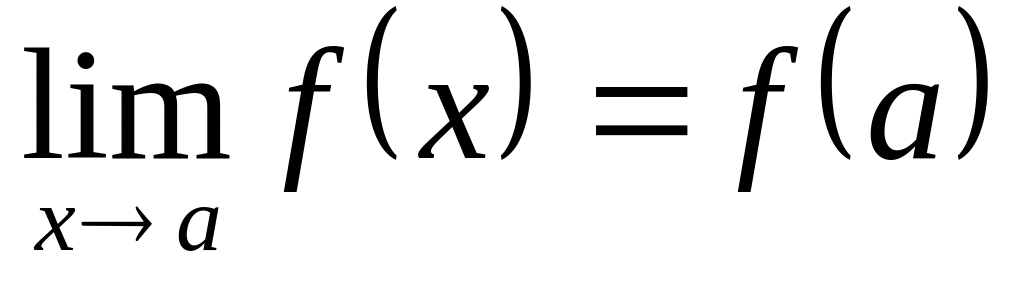Е сли хотя бы одно из этих условий не выполняется, то функция называется разрывной в точке а, а сама точка а называется точкой разрыва.
Если не существует, но существует оба односторонних предела в точке а, которые не равны друг другу, то разрыв в точке а называется разрывом первого рода или скачком.
Если хотя бы один из односторонних пределов не существуют или равен бесконечности, а, следовательно, не существует и , то разрыв в точке а называется разрывом второго рода.
Если
существует,
но функция f(x) в точке а не
определена или определена, но так, что
,
то разрыв в точке а называется
устранимым.
Рассмотрим функцию:
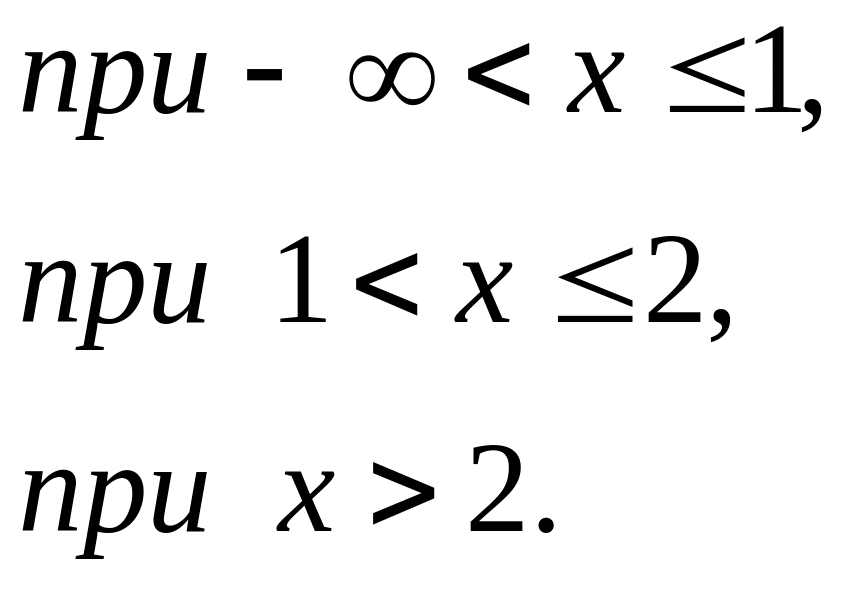
О
бласть
определения ее – вся числовая ось.
Разрывы возможны лишь в точках x =
1, x = 2, в которых функция изменяет
аналитическое выражение. Найдем
односторонние пределы в точках х =
1, х = 2.
При х = 1
;
так как f(1-0) = f(1+0) = 3, то в точке х
= 1 функция непрерывна.
При х = 2
;
,
так как f(2-0) ≠ f(2+0), то в точке
х = 2 функция имеет разрыв первого рода. Скачок функции в этой точке равен 1.
Асимптоты графика функции
Под асимптотой графика функции понимают такую прямую линию, к которой неограниченно приближаются точки графика функции у = f(x) по мере их удаления в ± ∞.
Если
,
то х = а – уравнение вертикальной
асимптоты.
Если
,
то у = b – уравнение горизонтальной
асимптоты.
Если
,
то у = kx + b – уравнение
наклонной асимптоты.
Производная и дифференциал
Производной функции у = f(х) по аргументу х называется предел отношения приращения функции к приращению независимого переменного при условии, что последнее стремится к нулю.
.
Дифференциалом dy функции у = f'(х) называется произведение производной этой функции на приращение независимого переменного Δх, т.е. dy = f'(х)Δх.
Дифференциал независимого переменного dx, по определению, равен приращению независимого переменного Δх, поэтому dy = f'(x)dx , т.е. дифференциал функции равен произведению производной функции на дифференциал независимого переменного.
Г
еометрический
смысл производной
Пусть у = f(х) – уравнение некоторой кривой, а М(x0;у0) – точка, лежащая на этой кривой, так что у0 = f(х0).
Производная f'(x0) численно равна тангенсу угла наклона касательной к графику функции, проведенной через точку М(x0;у0), т.е.
f '(x0) = tg α, где α – угол между касательной к данной кривой, проведенной через точку М, и положительным направлением оси абсцисс.
Уравнение касательной к данной кривой у = f(x), проходящей через точку М(x0;у0) кривой, имеет вид y - y0 = f’(x0) ∙ (x – x0).
Нормалью (MN) к кривой в данной точке М(x0;у0) называется перпендикуляр к касательной, проведенный через точку касания. Уравнение нормали (MN) записывается так:
.
Операция отыскания производной f '(x) данной функции f(x) называется дифференцированием этой функции. Пользуясь определением, можно получить таблицу формул дифференцирования элементарных функций:
,
n ≠ 0;
;
;
;
;
;
;
;
;
;
;
.
Правила дифференцирования функций
Производная постоянной величины равна нулю.
(С)' = 0.
Производная аргумента x равна 1.
x' = 1.
Производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
.
Производная произведения двух функций
.
Постоянный множитель выносится за знак производной.
.
Производная частного двух функций
.
Производная сложной функции. Пусть у есть функция от u:
у = f(u), где u – в свою очередь функция от аргумента x: u = φ(x).
В таком случае говорят, что у есть функция от функции. Записывают у = f(φ (x)). Если для соответствующих друг другу значений x и u существуют производные f '(u) и u' = φ '(x), то существует и производная от у по x, причем имеет место равенство у' = f '(u) · u'.
Второй производной называют производную от производной и обозначают у'' : у'' = (у')' . Дифференциал второго порядка обозначают : d2y = f ''(x) dx2
Пример выполнения задания 2
Найдём производные первого порядка указанных функций.
а ) у = arcsin2(ex).
=
.
б) .
.
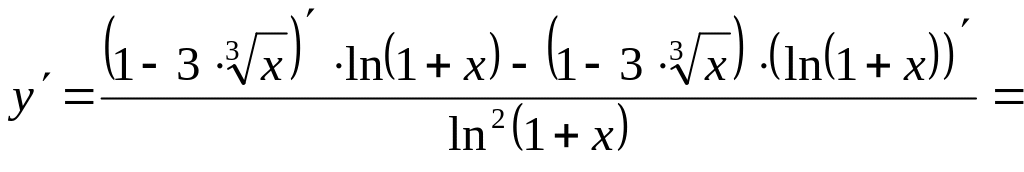
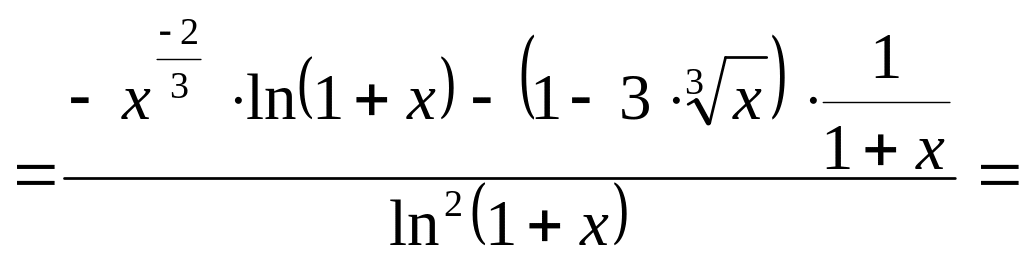
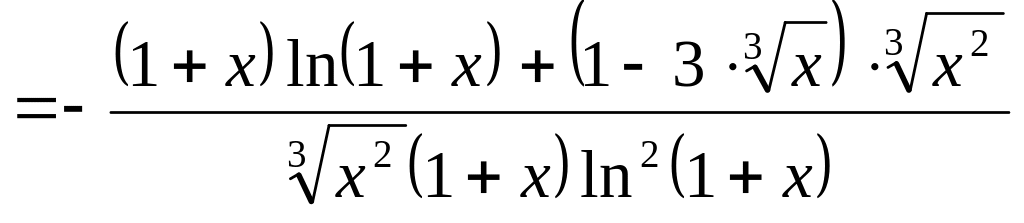в
)
.
.
г)
.
Прологарифмируем левую и правую части равенства по основанию е:
,
.
Дифференцируем, учитывая, что ln y – сложная функция, т.к.
у = у(х):
,
,
.
д) x3y2 + 5xy + 4 = 0.
Дифференцируем заданное соотношение, рассматривая у как функцию х:
.
Решаем полученное уравнение относительно у':
,
.
е)
Функция задана параметрически. Производная у'х от функции по переменной х вычисляется по формуле:
.
Используя данную формулу, найдем производную. Продифференцируем по t переменные х и у.
;
;
.
Пример выполнения задания 3
Найти дифференциал второго порядка функции у = ln(cos(5x)).
Дифференциал второго порядка определяется по формуле:
d2y = y''dx2.
Н
айдем
у' и
.
.
.
Сведения из теории
Схема исследования функций
Найти область определения функции.
Выяснить четность, нечетность, периодичность.
Исследовать функцию на непрерывность, найти точки
разрыва и выяснить характер разрывов.
Найти асимптоты графика функции.
Найти нули функции (у = 0) и интервалы знакопостоянства
(у > 0, y < 0).
Найти критические точки (у' = 0) и интервалы монотонности
(у' > 0, y' < 0).
Найти экстремумы функции.
Найти критические точки, в которых у'' = 0, и интервалы выпуклости и вогнутости.
Найти точки перегиба.
10. Выполнить схематический чертёж.
Пример выполнения задания 4
Исследуем функцию: и построим её график.
Решение.
Найдем первую и вторую производные этой функции.
.
.
1. Область определения:
.
2. Функция общего вида, непериодическая.
3. Точка разрыва функции х = 0.
,
в точке х = 0 разрыв второго рода.
4. , х = 0 – вертикальная асимптота.
– горизонтальной асимптоты нет.
,
k = 1,
,
b = 0,
у = х – наклонная асимптота.
5. у = 0.
,
.
y > 0 ,
при
;
y < 0 , при
6.
.
,
,
x = 2,
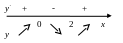
7. ymin(2) = 3.
при x
(-∞; 0) функция возрастает;
при x (0; 2) функция убывает;
при x (2; +∞) функция возрастает.
8. у''
= 0;
≠
0 – точек перегиба
нет. При х = 0 вторая
производная не существует.
9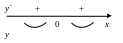
.
График
функции при
является
вогнутым.
График функции имеет вид, указанный на рисунке.
Пример выполнения задания 5
Выполним над комплексными числами указанные действия:
а) ;
Воспользуемся формулой:
,
где k = 0,1,…, n-1.
Запишем
комплексное число, заданное в алгебраической
форме, в тригонометрической форме:
,
где
,
,
,
.
Для данного
числа
;
;
.
Следовательно,
.
,
k = 0, 1, 2.
б) .
Воспользуемся формулой:
.
Запишем данное комплексное число в тригонометрической форме.
,
;
;
.
Следовательно,
.
.