Модуль 2

Аналитическая геометрия на плоскости

и в пространстве

Задачи для решения

Задание 1

Дана кривая второго порядка. Найти ее вершины, фокусы, эксцентриситет. Для гиперболы составить уравнение асимптот. Построить кривую второго порядка.

Варианты

1. 9x² + 16y² = 144;

2. 4x² – 9y² = 36;

3. 9x² + 25y² = 225;

4. 16x² – 9y² = 144;

5. x² +4y² = 16;

6. 25x² – 49y² = 1225;

7. 16x² +9y² = 144;

8. 16x² – 25y² = 400;

9. 9x² +4y² = 36;

10. 25x² – 16y² = 400.

Задание 2

Найти вершину, ось симметрии, фокус и директрису параболы. Сделать чертеж.

Варианты

1. y = 4x² - 8x + 7;

2. y² – 2y +5 = 2x;

3. y = x² +4x + 12;

4. y² – x – 6y +17 = 0;

5. y² + 8x – 16 = 0;

6. y² – 10x - 2y – 19 = 0;

7. x² +4x +6y – 20 = 0;

8. y² – 6x + 14y + 49 = 0;

9. x² – 6x – 4y + 29 = 0;

10. x² + 8x + 6y + 46 = 0.

Задание 3

Даны координаты вершин пирамиды А_1,А₂ А₃ А₄.

, , , .

Найти:

а) уравнение ребра [A₁A₂];

б) уравнение грани А₁А₂А₃;

в) угол между ребром [A₁A₄] и гранью А₁А₂А₃;

г) уравнение высоты h, опущенной из вершины А₄ на грань

А₁А₂А₃;

д) длину d высоты h.

Варианты

1. А₁(3,1,4), А₂ (-1,6,1), А₃ (-1,1,6), А₄(0,4,-1);

2. А₁ (3,3,9), А₂ (6,9,1), А₃(1,7,3), А₄(8,5,8);

3. А₁(3,5,4), А₂ (5,8,3), А₃ (1,9,9), А₄(6,4,8);

4. А₁ (2,4,3), А₂ (7,6,3), А₃ (4,9,3), А₄(3,6,7);

5. А₁ (9,5,5), А₂ (-3,7,1), А₃(5,7,8), А₄(6,9,12);

6. А₁ (0,7,1), А₂ (4,1,5), А₃ (4,6,3), А₄(3,9,8);

7. А₁ (5,5,4), А₂ (3,8,4), А₃(3,5,10), А₄(5,8,2);

8. А₁(6,1,1), А₂(4,6,6), А₃(4,2,0), А₄(1,2,6);

9. А₁(7,5,3), А₂ (9,4,4), А₃ (4,5,7), А₄(7,9,6);

10. А₁(6,6,2), А₂(5,4,7), А₃(2,4,7), А₄(7,3,0).

Решение типовых задач

Задание 1

Дана кривая второго порядка. Найти ее вершины, фокусы, эксцентриситет. Для гиперболы составить уравнение асимптот. Построить кривую второго порядка.

а) 3x² + 4y² = 12; б) 9x² – 16y² = 144.

Задание 2

Найти вершину, ось симметрии, фокус и директрису параболы. Сделать чертеж.

Уравнение параболы y² – 2x + 4y + 2 = 0.

Задание 3

Даны координаты вершин пирамиды А₁ А₂ А₃ А₄.

, , , .

Найти:

а) уравнение ребра [A₁A₂];

б) уравнение грани А₁А₂А₃;

в) угол между ребром [A₁A₄] и гранью А₁А₂А₃;

г) уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃;

д) длину высоты.

Пример выполнения задания 1

a) Дана кривая второго порядка:

3x² + 4y² = 12.

Это уравнение эллипса. Преобразуем его к каноническому виду .

Разделим обе части уравнения на 12: . Каноническое уравнение имеет вид: .

Большая полуось эллипса а = 2, а малая полуось .

Следовательно, координаты его вершин:

А₁(-2; 0), А₂(2; 0), В₁(0; ), В₂(0; ).

Координаты фокусов: F₁(-с; 0) ; F₂(с; 0).

Найдем с по формуле: ; .

Координаты фокусов: F₁(-1; 0) ; F₂(1; 0).

Эксцентриситет эллипса: .

б) Дана кривая второго порядка:

9x² – 16y² = 144.

Это уравнение гиперболы. Преобразуем его к каноническому виду .

Разделим обе части уравнения на 144: .

Полуоси данной гиперболы: действительная а = 4, мнимая b=3. Следовательно, ее вершины:

А₁(-4;0), А₂(4;0), В₁(0;-3), В₂(0;3).

Прямоугольник с центром в начале координат, сторонами, параллельными координатным осям и проходящими через вершины гиперболы, называется основным прямоугольником гиперболы. Его диагонали являются асимптотами гиперболы.

Асимптоты: .

Координаты фокусов: F₁(-с; 0) ; F₂(с; 0).

Найдем с по формуле: ; , следовательно, F₁(-5;0); F₂(5;0).

Эксцентриситет гиперболы .

Пример выполнения задания 2

Найдём вершину, ось симметрии, фокус и директрису параболы

y² – 2x + 4y + 2 = 0.

Приведем уравнение параболы к каноническому виду

. Здесь – координаты вершины,

р – параметр параболы (расстояние между фокусом и директрисой).

Выделим в уравнении параболы полный квадрат по у:

y² +4y + 4 – 2x – 4 + 2 = 0,

(y + 2)² = 2x + 2.

Каноническое уравнение:

(y + 2)² = 2(x + 1).

Координаты вершины О₁(-1;-2). Парабола симметрична относительно прямой у = -2. Величина параметра р = 1.

Если вершина параболы находится в точке (0,0), то координаты её фокуса: F(p/2;0), уравнение директрисы: х = -р/2. Следовательно, наша парабола имеет фокус в точке .

Уравнение директрисы .

Пример выполнения задания 3

Даны координаты вершин пирамиды А₁А₂А₃А₄:

А₁(0,0,1), А₂ (2,3,5), А₃ (6,2,3), А₄(3,7,2).

а) Канонические уравнения прямой, проходящей через точки А₁(х₁, у₁, z₁) и А₂(х₂, у₂, z₂) имеют вид:

.

Следовательно, уравнение ребра [ ], как уравнение прямой имеет вид:

, или .

б) Составим уравнение плоскости А₁А₂А₃ как уравнение плоскости, проходящей через три данные точки , , :

.

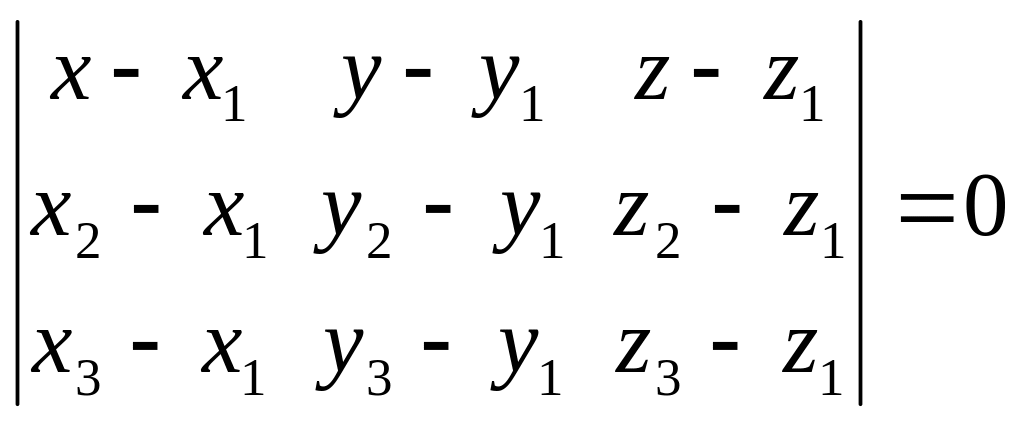Получим:

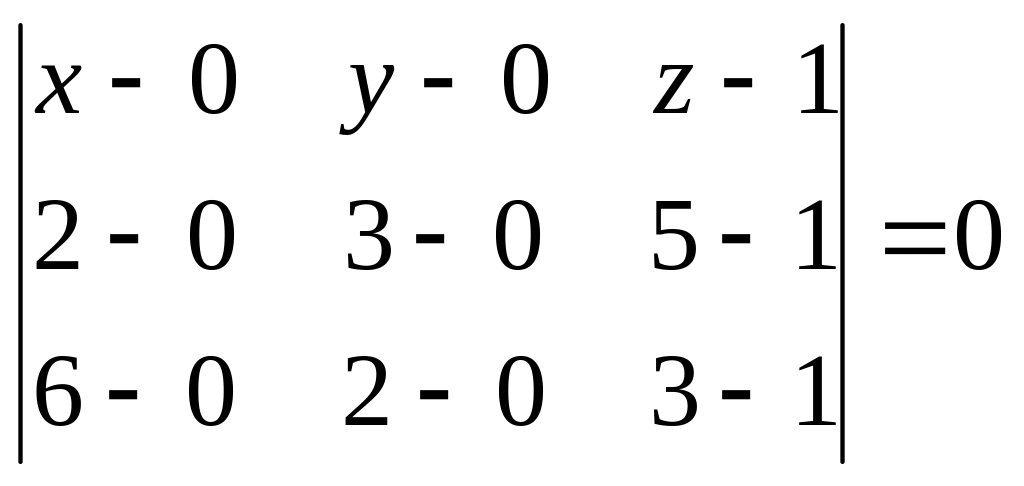, т.е. .

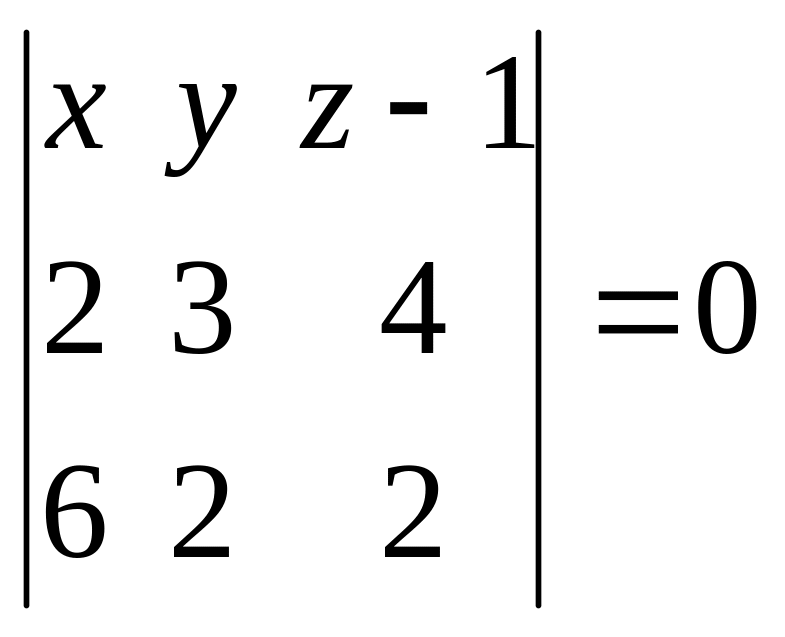Приведём это уравнение к общему виду:

,

x(6 - 8) – y(4 – 24) + (z – 1)(4 – 18) = . Разделим последнее равенство на –2 и получим общее уравнение плоскости А₁А₂А₃: x – 10y + 7z – 7 = 0.

б) Угол между ребром [A₁A₄] и гранью А₁А₂А₃ определим как угол между прямой и плоскостью . Синус этого угла находим по формуле:

.

Уравнение ребра [A₁A₄] находим аналогично уравнению [ ]: .

Уравнение плоскости А₁А₂А₃: x – 10y + 7z – 7 = 0.

.

.

.

г) Составим уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А_3, как уравнения прямой, проходящей через точку А₄:

, перпендикулярно плоскости А₁А₂А₃ .

Для нахождения m, n, p используем условие перпендикулярности прямой и плоскости .

Уравнение прямой: .

Уравнение плоскости: x – 10y + 7z – 7 = 0.

Так как А = 1, В = -10, С = 7, то m = 1, n = -10, p = 7.

Следовательно, уравнение высоты имеет вид:

.

д ) Длину высоты определим по формуле для вычисления расстояния d от точки до плоскости А₁А₂А₃ .

.

Координаты точки А₄(3,7,2).

Уравнение плоскости А₁А₂А₃: x – 10y + 7z – 7 = 0.

Следовательно,

= .

Модуль 3

Введение в математический анализ. Дифференциальное исчисление функций одной переменной