Нормальный (гауссовский) закон распределения. Кривая нормального распределения.
Если случайная величина X есть результат суммирования множества случайных величин с произвольными законами распределения, причем каждая из них играет примерно одинаковую роль в сумме, то закон распределения случайной величины X близок к закону распределения, называемому нормальным (гауссовским).
При нормальном (гауссовском) законе плотность распределения задаётся формулой:
,
где т - математическое ожидание случайной величины, σ -среднее квадратическое отклонение.
Вероятность попадания случайной величины на заданный участок
Вероятность попадания случайной величины в интервал (α;β) равна приращению её функции распределения на этом интервале:
P(a<X< β) = F(β) - F(a).
Если случайная величина подчинена нормальному закону, часто вместо её функции распределения применяется функция Лапласа.
Выражение
.
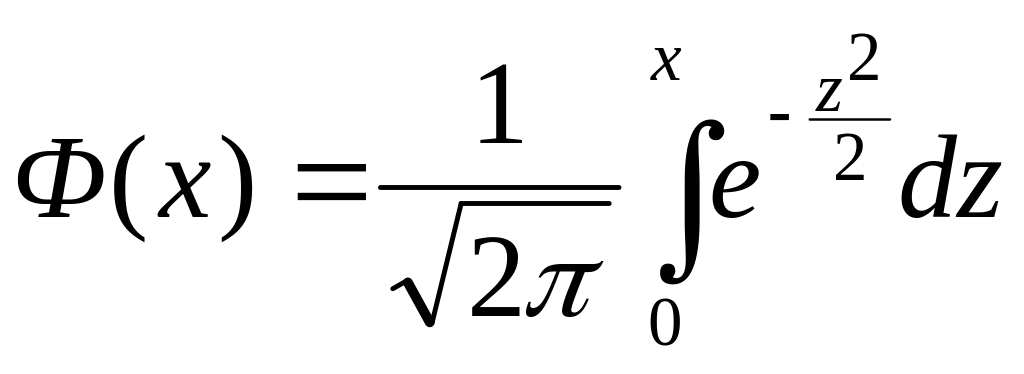называется функцией Лапласа. В справочниках функция Лапласа задана таблицей. Вероятность попадания нормальной случайной величины в интервал (α;β) определяется по формуле
Значения функции Лапласа.
х |
Ф(х) |
х |
Ф(х) |
х |
Ф(х) |
0.0 |
0.0000 |
1.00 |
0.3413 |
2,0 |
0,4772 |
0.05 |
0199 |
1.05 |
3531 |
2.1 |
4821 |
0.10 |
0398 |
1.10 |
3643 |
2.2 |
4861 |
0.15 |
0596 |
1.15 |
3749 |
2.3 |
4892 |
0.20 |
0792 |
1.20 |
3849 |
2.4 |
4918 |
0.25 |
0987 |
1.25 |
3945 |
2.5 |
4935 |
0.30 |
1179 |
1.30 |
4032 |
2.6 |
4953 |
0.35 |
1368 |
1.35 |
4114 |
2.7 |
4965 |
х |
Ф(х) |
х |
Ф(х) |
х |
Ф(х) |
0.40 |
1554 |
1.40 |
4192 |
2.8 |
4974 |
0.45 |
1736 |
1.45 |
4264 |
2.9 |
4981 |
0.50 |
1914 |
1.50 |
4331 |
3.0 |
4986 |
0.55 |
2088 |
1.55 |
4394 |
3.1 |
4990 |
0.60 |
2257 |
1.60 |
4452 |
3.2 |
4993 |
0.65 |
2421 |
1.65 |
4505 |
3.3 |
4995 |
0.70 |
2580 |
1.70 |
4554 |
3.4 |
4996 |
0.75 |
2733 |
1.75 |
5499 |
3.5 |
4997 |
0.80 |
2881 |
1.80 |
4640 |
4.0 |
4999 |
0.85 |
3023 |
1.85 |
4678 |
4.5 |
4999 |
0.90 |
3159 |
1.90 |
4712 |
5.0 |
4999 |
0.95 |
3289 |
1.95 |
4744 |
|
|
Пример выполнения задания 1
У рабочего 20 однотипных деталей, из которых окрашено в красный цвет 9 деталей, в зеленый цвет 7 деталей и в синий 4 детали. Рабочий наудачу берет 6 деталей. Найти вероятность того, что среди выбранных деталей окажется 3 красных, 2 зеленых и 1 синяя.
Решение.
Обозначим буквой А то событие, вероятность которого требуется найти по условию задачи. Вероятность события равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:
.
Общее число возможных элементарных исходов п равно числу способов, которыми можно извлечь 6 деталей из 20, т.е. равно
Число т исходов, благоприятствующих интересующему нас событию:
.
Тогда:
Пример выполнения задания 2
В читальном зале имеется 6 учебников по теории вероятностей, из которых 3 в твёрдом переплете. Библиотекарь наудачу взял 2 учебника. Найти вероятность того, что оба учебника окажутся в твёрдом переплете.
Решение.
Введем обозначение событий. Обозначим буквой А то событие, вероятность которого надо найти:
- {первый взятый учебник имеет твёрдый
переплет}.
- {второй взятый учебник имеет твёрдый
переплет}.
Вероятность того, что первый учебник
имеет твёрдый переплет, равна
.
Вероятность того, что второй учебник
имеет твёрдый переплет, при условии,
что первый взятый учебник был в твёрдом
переплете, т.е. условная вероятность
события
,
равна
.
Искомая вероятность того, что оба учебника имеют твёрдый переплет, по теореме умножения вероятностей зависимых событий равна
.
Пример выполнения задания 3
В пирамиде установлены 10 винтовок, из которых 4 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95. Для винтовки без оптического прицела эта вероятность равна 0,8. Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее: стрелок стрелял из винтовки с оптическим прицелом или без него?
Решение.
Обозначим события:
А – {стрелок поразил мишень}.
Гипотезы:
- {стрелок взял для стрельбы винтовку с
оптическим прицелом};
- {стрелок взял для стрельбы винтовку
без оптического прицела}.
Вероятности гипотез равны:
;
;
Условные вероятности гипотез соответственно равны:
;
.
Вероятность того, что стрелок поразил мишень из наудачу взятой винтовки, по формуле полной вероятности равна:
Вероятность того, что стрелок поразил мишень из винтовки с оптическим прицелом, по формуле Байеса равна:
.
Вероятность того, что стрелок поразил мишень из винтовки без оптического прицела, по формуле Байеса равна:
.
Ответ: Вероятнее, что винтовка была без оптического прицела.
Пример выполнения задания 4
По цели производится 5 независимых выстрелов. Вероятность попадания в цель при одном выстреле равна 0,6. Для получения зачета по стрельбе требуется не менее трех попаданий. Найти вероятность получения зачета.
Решение:
Искомая вероятность находится по формуле
.
Пример выполнения задания 5
Два стрелка сделали по одному выстрелу в мишень. Вероятность попадания для первого стрелка 0,3; для второго – 0,4.
Для случайного числа попаданий в цель составить ряд и функцию распределения. Построить их графики. Найти M[x], D[x], σ[x].
Решение.
Случайная величина Х – число попаданий: X={0, 1, 2};
x=0 {никто не попал в мишень}:
;
х=1 {в мишень попал один стрелок}:
х=2 {в мишень попали оба стрелка}:
Ряд распределения:
Х |
0 |
1 |
2 |
Р |
0,42 |
0,46 |
0,12 |
Найдем функцию распределения:
х ≤ 0: F(х) = Р(x < 0) = 0;
0 < x ≤ 1: F(x) = P(x = 0) =0,42;
1< x ≤ 2: F(x) = P(x = 0) + P(x = 1) = 0,42+0,46=0,88;
x > 2: F(x) = P(x = 0) + P(x = 1) + P(x = 2) = 0,42+0,46+0,12 = 1.
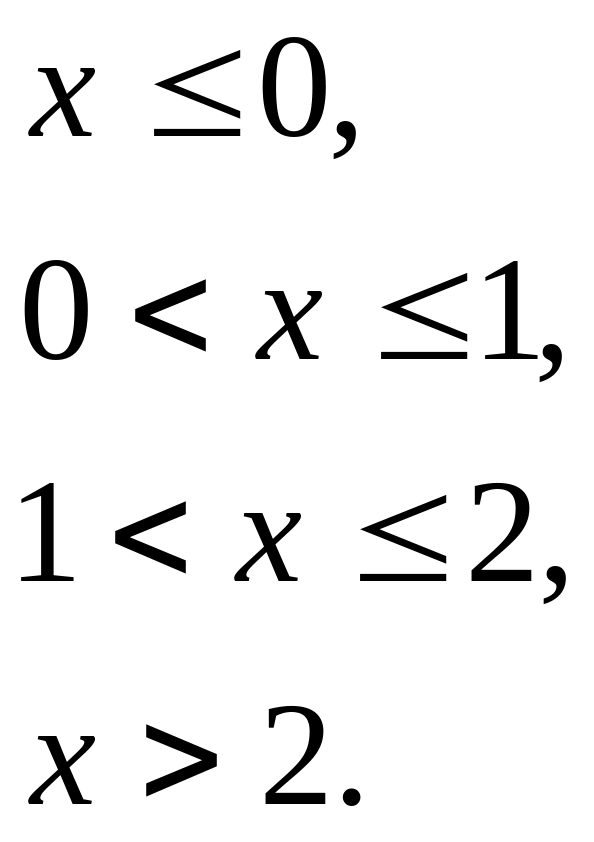
Многоугольник распределения имеет вид:
Р 0,46 0,42
0,12
1 2 X
График функции F(х) имеет вид:
Математическое ожидание:
Дисперсия:
.
Среднее квадратическое отклонение:
.
Пример выполнения задания 6
Непрерывная случайная величина задана плотностью распределения:
Требуется:
1) определить коэффициент с;
2) найти функцию распределения F(х);
3) построить графики f(х) и F(х);
4) найти вероятность того, что случайная величина Х принимает
значения из интервала (1; 2).
Решение.
1) Для определения
коэффициента с используем свойство
плотности распределения
.
.
Получим:
.
2) Функцию распределения F(х) определяем по свойству плотности распределения
.
а) случайная величина попадает на интервал (- ∞; 0):
.
б) случайная величина попадает на интервал (0; 2):
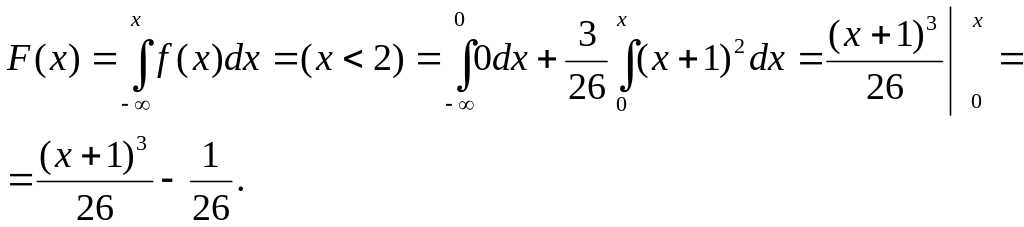
в) случайная величина попадает на интервал (2; +∞):
Таким образом,
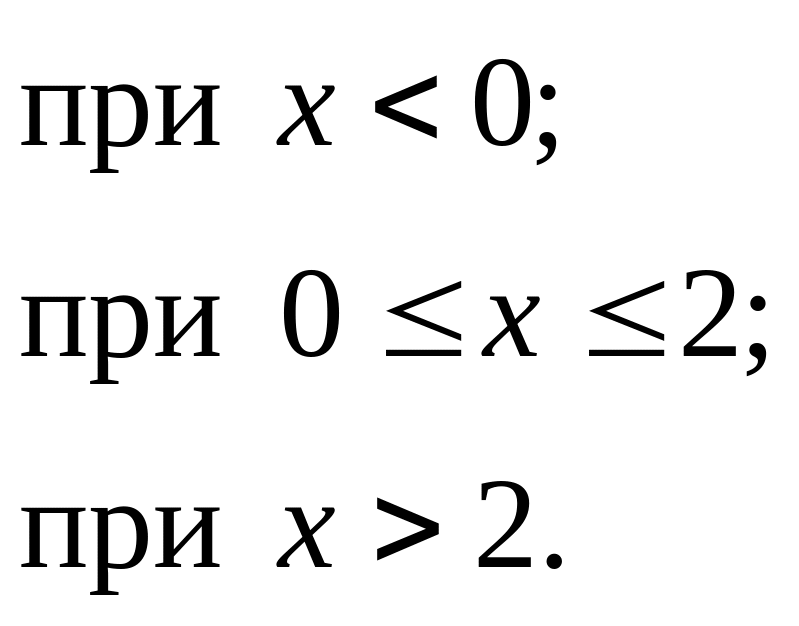
3
)
Графики функций f(х) и F(х):
y=f(x)
4) Р(α<x<β) = F(β) - F(α).
P(1<
x <2)=F(2)
– F(1) =
.
Пример выполнения задания 7
Случайная величина подчинена нормальному закону с параметрами т = 3 и σ = 2. Составить плотность распределения этой случайной величины f(х) и найти вероятность того, что случайная величина попадет в интервал (- 1; 4).
Решение.
Запишем плотность нормального распределения в общем виде:
,
значит
.
Вероятность попадания нормально распределенной случайной величины Х в интервал (α; β) вычисляется по формуле:
Следовательно,
0,1915
+ 0,4772 = 0,6687.