
- •Контрольные задания и методические рекомендации для студентов заочного обучения Севастополь 2013 г.
- •I семестр
- •Модуль 1 Линейная алгебра. Векторная алгебра Задачи для решения.
- •Решение типовых задач Задание 1
- •Задание 2
- •Модуль 2
- •Задачи для решения
- •Решение типовых задач
- •Задачи для решения
- •Определение предела функции
- •Непрерывность функции
- •II семестр
- •Повторное дифференцирование.
- •Модуль 4
- •Задачи для решения Задание 1
- •Решение типовых задач Задание 1
- •Задание 2
- •Задание 3
- •Задачи для решения Задание 1
- •Задание 3
- •Решение типовых задач
- •Задачи для решения
- •Задание 2
- •Задание 3
- •Решение типовых задач
- •Задание 2
- •III семестр
- •Задачи для решения
- •Варианты
- •Варианты
- •Варианты
- •Решение типовых задач
- •Дифференциальные уравнения первого порядка
- •Дифференциальные уравнения высших порядков Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Задачи для решения
- •Варианты
- •Решение типовых задач
- •Решение типовых задач
- •Числовые ряды
- •Обобщенно-гармонический ряд:
- •Ряды Фурье
- •IV семестр
- •Модуль 9 Операционное исчисление Задачи для решения
- •Решение типовых задач
- •Свойства преобразования Лапласа
- •Теория вероятностей Задачи для решения
- •Решение типовых задач
- •Сведения из теории
- •Нормальный (гауссовский) закон распределения. Кривая нормального распределения.
- •Литература
Задачи для решения
Задание 1
Исследовать на сходимость числовые ряды.
Варианты
а)
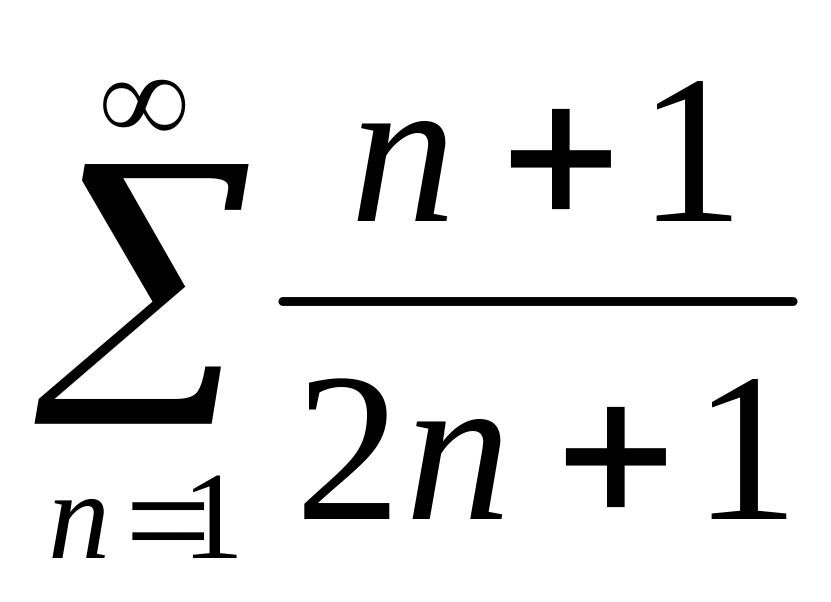 ; б)
; б)
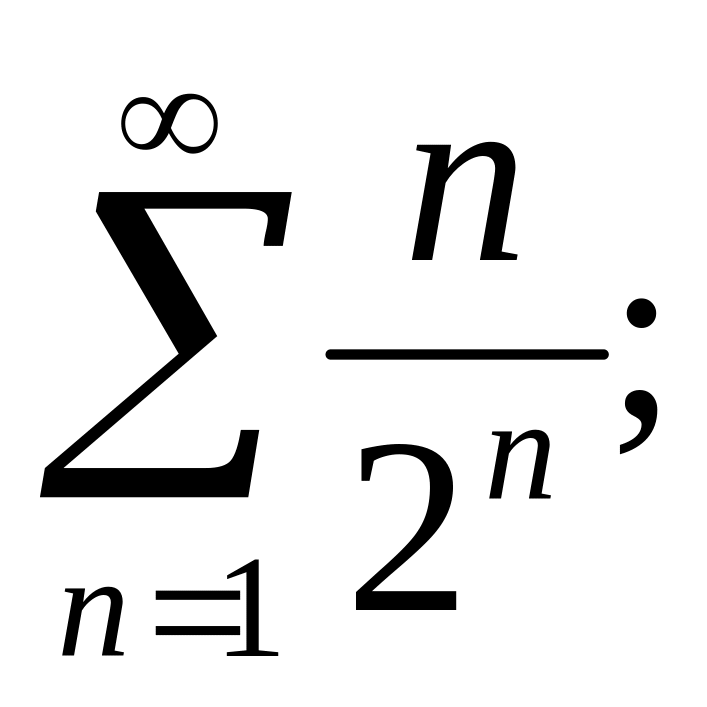
в)
![]() ; г)
; г)
![]() .
.
2. а)
![]() ; б)
; б)
![]()
в)
![]() ; г)
; г)
![]() .
.
3. а)
![]() ; б)
; б)
![]()
в)
![]() г)
г)
![]() .
.
4. а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]() .
.
5. а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]() .
.
6. а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]() .
.
7. а)
![]() б)
б)
![]()
в)
![]() ;
г)
;
г)
![]() .
.
8. а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]() .
.
9. а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]() .
.
10. а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]() .
.
Задание 2
Определить радиус и область сходимости степенных рядов.
Варианты
1. а)
![]() ;
б)
;
б)
![]() .
.
2. а)
![]() ;
б)
;
б)
![]() .
.
3. а)
![]() ;
б)
;
б)
![]() .
.
4. а)
![]() ;
б)
;
б)
![]() .
.
5. а)
![]() ;
б)
;
б)
![]() .
.
6. а)
![]() ;
б)
;
б)
![]() .
.
7. а)
![]() ;
б)
;
б)
![]() .
.
8. а)
![]() ; б)
; б)
![]() .
.
9. а)
![]() ;
б)
;
б)
![]() .
.
10. а)
![]() ; б)
; б)
![]() .
.
Задание 3
Разложить заданную функцию в ряд Фурье в интервале [-π; π].
Варианты
1. a)
![]()
![]()
![]()
![]()
б) f(x) = 2x на отрезке [0;2] по косинусам.
2. a)
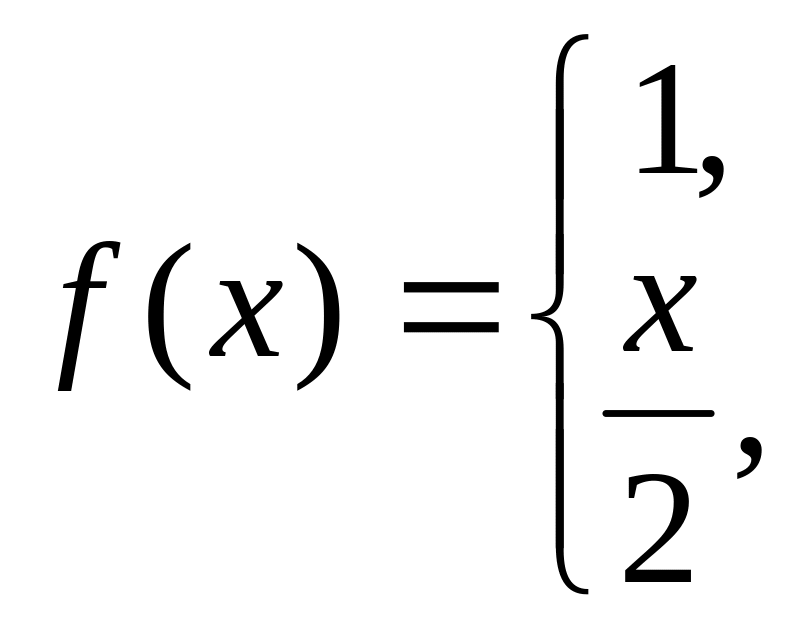
б) f(x) = 1 – x на отрезке [0;1] по синусам.
3. a)
![]()
б)
![]() на отрезке [0;4] по косинусам.
на отрезке [0;4] по косинусам.
4. a)
![]()
б) f(x) = x – 1 на отрезке [0;1] по косинусам.
5. a)
![]()
б) f(x) = 2 – 2x на отрезке [0;1] по синусам.
6. а)
![]()
б)
![]() на отрезке [-5;0] по косинусам.
на отрезке [-5;0] по косинусам.
7. а)
![]()
б) f(x) = 3 – x, на отрезке [0;3] по синусам.
8. а)
![]()
б) f(x) = 1 – 2x на отрезке [0;1/2] по косинусам.
9. а)
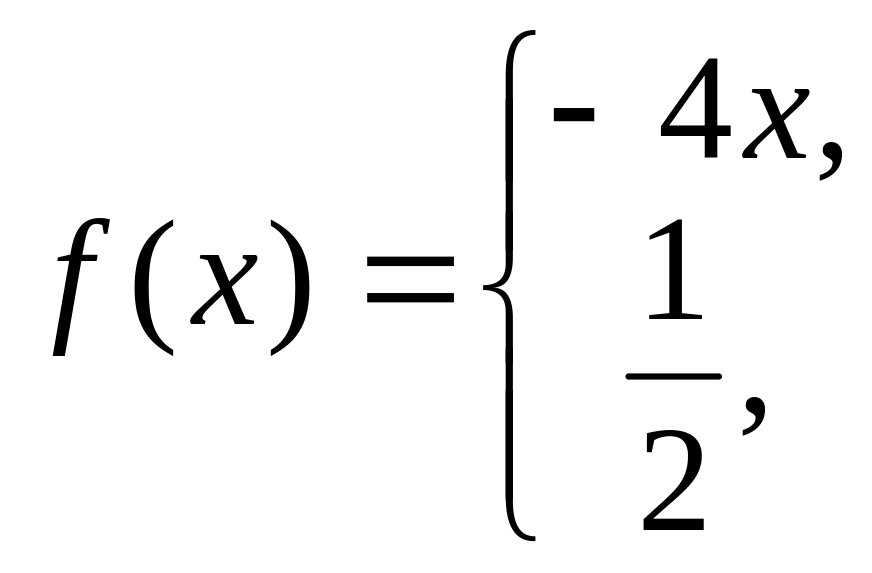
б) f(x) = -2x на отрезке [0;1/2] по синусам.
10. а)
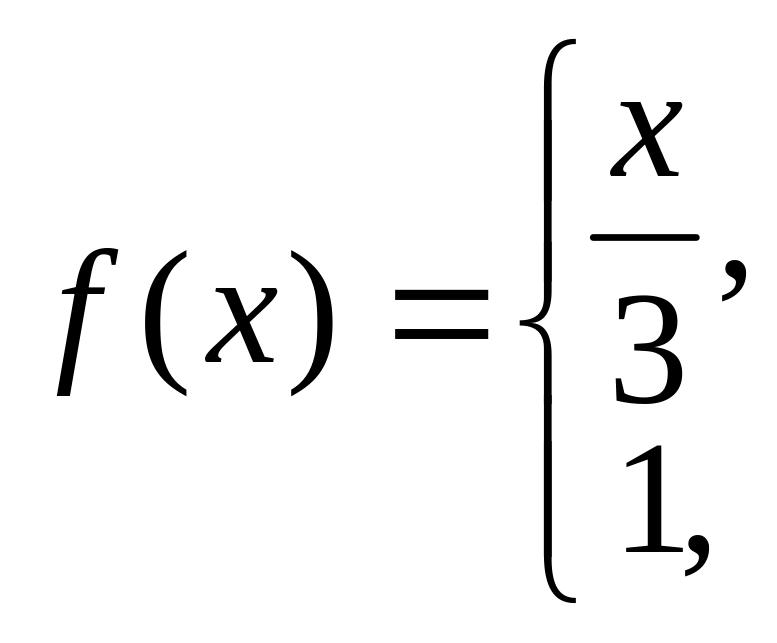
б)
![]() на отрезке [0;4] по косинусам.
на отрезке [0;4] по косинусам.
Решение типовых задач
Задание 1
Исследовать на сходимость числовые ряды.
а)
![]() ;
;
б)
![]()
![]() +…;
+…;
в)
![]() .
.
Задание 2
Определить
радиус и область сходимости степенного
ряда
![]() .
.
Задание 3
Разложить
функцию
![]()
![]() в ряд Фурье в интервале [-π; π].
в ряд Фурье в интервале [-π; π].
Решение типовых задач
Сведения из теории
Числовые ряды
Числовым рядом называют сумму бесконечной числовой последовательности вида
![]() =
=
![]() .
.
Числа
![]() называют членами ряда, un –
общим членом ряда.
называют членами ряда, un –
общим членом ряда.
Конечная сумма
Sn
=
![]() называется n-ой частичной
суммой ряда.
называется n-ой частичной
суммой ряда.
Если существует
конечный предел
![]() , ряд называется сходящимся, в противном
случае – расходящимся.
, ряд называется сходящимся, в противном
случае – расходящимся.
Необходимый признак сходимости
Если ряд
сходится, то его общий член un
стремится к нулю при n → ∞, т.е.
![]() .
.
Указанный признак не является достаточным, т.е. если un → 0, то о сходимости ряда ничего сказать нельзя.
Достаточные признаки
Признак сравнения
Если даны два ряда
и
![]() с положительными членами, причем члены
первого ряда не превосходят соответствующих
членов второго ряда: 0 ≤ un
≤ vn , то
с положительными членами, причем члены
первого ряда не превосходят соответствующих
членов второго ряда: 0 ≤ un
≤ vn , то
а) из сходимости второго ряда следует сходимость первого ряда;
б) из расходимости первого ряда следует расходимость второго ряда.
Для сравнения часто используются ряды:
Ряд геометрической прогрессии:
![]()
![]()
