9.4. Выявление сезонности с использованием сезонных фиктивных переменных в модуле Multiple regression

Для выявления описания сезонных колебаний на практике используют фиктивные переменные. При этом модель имеет следующий вид:

= а₀ + а₁t + c₂Z₂ + c₃Z₃ + c₄Z₄ + _t (9.1)

где:

а₀, а₁, с₂, с₃, с₄ - коэффициенты модели;

В приведенной формуле 1-й квартал взят в качестве эталонной категории, а фиктивные переменные позволят оценить разницу в уровнях се­зонности между эталонным кварталом и остальными.

Регрессионная модель, описывающая динамику уровней ряда, относящихся к эталонному 1-му кварталу, примет вид:

y_t=a₀+а₁t

соответственно для наблюдений

2-го квартала y_t=a₀ + а₁t +c₂;

3-го квартала y_t= a₀ + а₁t +c₃;

4-го квартала y_t= a₀ + а₁t +c₄;

Переход из одного квартала в другой будет отражаться лишь в изменении свободного члена регрессионного уравнения и не бу­дет касаться значения параметра b, определяющего угол наклона линейного тренда и характеризующего средний абсолютный при­рост уровней ряда под воздействием тенденции.

Найденные значения коэффициентов с₂, с₃, с₄ позволяют оце­нить «сдвиги» в уровнях за счет фактора сезонности относительно i-го, эталонного квартала. Можно усреднить четыре полученные линии регрессии:

(9.2)

Тогда расстояние между отдельной регрессионной прямой для любого квартала и усредненной моделью, даст оценку сезонных отклонений в этом квартале. Очевидно, что для аддитивной модели сумма сезонных отклонений будет равна нулю.

Рассмотрим реализацию применения фиктивных переменных для моделирования сезонных колебаний в пакете STATISTICA.

В качестве исходных данных используем квартальный ряд динамики ВВП (приложение Р, таблица Р.2) с 1 квартала 1999 г. до 4 квартала 2004 г.

Шаг 1. Для начала проведем визуализацию ряда, для этого в главном меню программы выберем Graphs  2D Graphs®Line Plots (Variables). После выбора переменной (кнопка Variables) на основе которой необходимо построить график (в данном случае это переменная Y), получаем следующий результат:

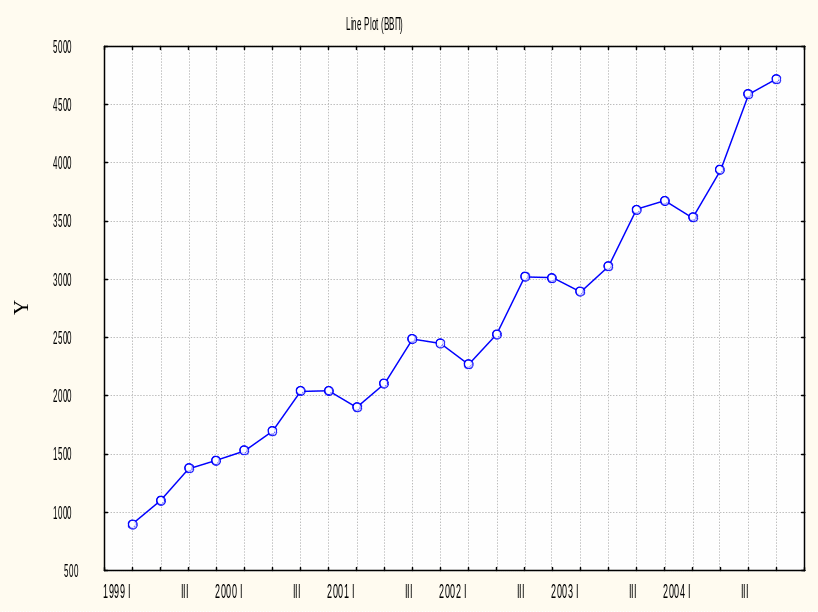
Рисунок 9.2 - Динамика ВВП России 1 квартала 1999г-4 квартал 2004г

Согласно приведенному графику наблюдается значительный рост показателя за анализируемый период, а также сезонность с пиком в каждом 3 квартале года.

Шаг 2. Для описания сезонных колебаний создадим 4 фиктивных переменных. Для этого переходим в рабочую таблицу и образуем, переменную t – характеризующую моменты (периоды) времени переменные и переменные Z2, Z3 и Z4 – характеризующие сезонность в анализируемом ряду:

Рисунок 9.3 – Рабочая таблица с набором фиктивных переменных (приведена часть исходного окна)

Шаг 3. В главном меню выберем: Statistics  Multiple Regression (Статистика  Множественная регрессия). В появившемся окне Multiple Linear Regression необходимо нажать кнопку Variables (Переменные) и указать в качестве зависимой переменной (Dependent var.) Y, а в качестве не зависимых (Independent var.) переменных - t, Z2, Z3 и Z4.

Нажав кнопку ОК, перейдем в следующее окно, содержащее результаты построения модели.

Шаг 4. В появившемся окне Multiple Regression Results выберем кнопку Summary: Regression results (Итоги: Результаты построения регрессии) перейдем к двум таблицам содержащим оцененные параметры модели и основные показатели адекватности построения регрессии.

Таблица 9.4 – Показатели адекватности модели

Statistic	Value
Multiple R	0,989
Multiple R?	0,977
Adjusted R?	0,973
F(11,144)	204,893
p	0,000
Std.Err. of Estimate	174,096

Согласно данным, приведенным в таблице 9.5 полученная модель статистически значима по F-критерию Фишера, но параметр при фиктивной переменной Z2 не проходит тест на статистическую значимость по t-критерию Стьюдента.

Таблица 9.5 – Результаты оценивания сезонной модели

	Beta	Std.Err. of Beta	B	Std.Err. of B	t(19)	p-level
Intercept			606,006	91,247	6,641	0,000
t	0,956	0,035	142,156	5,202	27,327	0,000
Z2	0,043	0,042	101,828	100,649	1,012	0,324
Z3	0,168	0,043	398,189	101,051	3,940	0,001
Z4	0,125	0,043	296,600	101,718	2,916	0,009

В общем, опираясь на построенную модель можно сказать, что в анализируемом ряду присутствует сезонность, с максимум в 3 квартале каждого года, т.к. -коэффициент при Z3 имеет наибольшее значение.