Уравнение плоскости, проходящей через три точки

Пусть – три точки пространства, не лежащие на одной прямой, через которые проходит плоскость. Возьмем произвольную точку плоскости и образуем три вектора . Так как все 4 точки лежат в одной плоскости, то и три вектора, их соединяющие, лежат в той же плоскости, то есть компланарны. Их смешанное произведение равно 0, т.е.

Поскольку смешанное произведение равно определителю, составленному из координат векторов, то должно выполняться:

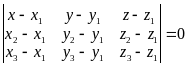
Написанное равенство – уравнение плоскости, проходящей через три заданные точки.

Покажем на примере как от данного вида уравнения плоскости, довольно громоздкого и неудобного на практике, перейти к общему.

Пример. Составить уравнение плоскости, проходящей через три точки .

Подставив в (19.4) координаты точек , получим:

.

Разложим определитель по элементам первой строки:

,

,

.

Сократив на 5, получим общее уравнение искомой плоскости

.

Угол между плоскостями

Пусть даны две плоскости и :

с нормальными векторами . Тогда  – двугранный угол между ними, – равен углу, образованному нормальными векторами . Поэтому

.

Пример. Найти угол между плоскостями

.

Подставив параметры уравнений плоскостей в соответствующую формулу, имеем

.

Отсюда находим, что .

Кратчайшее расстояние от точки до плоскости

Найдем расстояние d от точки до плоскости Р.

Под расстоянием от точки до плоскости понимается длина отрезка перпендикуляра, опущенного из этой точки на плоскость. Возьмем на плоскости, заданной уравнением , произвольную точку и соединим ее вектором с M₀, а из основания перпендикуляра отложим вектор , нормальный плоскости. Тогда расстояние d будет равно абсолютной величине проекции вектора на направление вектора , обозначаемой . Данную проекцию можно найти, используя скалярное произведение двух векторов

.

Вычисляя скалярное произведение через координаты векторов, получим

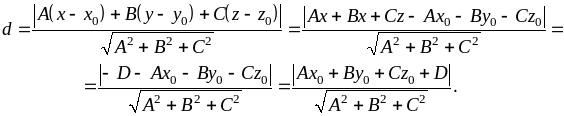
Здесь использовано равенство , вытекающее из уравнения плоскости.

Пример. Найти расстояние от точки до плоскости .

Подставив необходимые данные в формулу, имеем

.

3.1.2. Прямая в пространстве

Под уравнениями прямой в пространстве будем понимать соотношения между координатами произвольной точки, принадлежащей данной прямой.

Канонические уравнения прямой

Положение прямой L в пространстве можно однозначно определить, в частности, заданием какой-либо ее фиксированной точки М₀ и ненулевого вектора , коллинеарного этой прямой. Такой вектор называется направляющим вектором прямой.

П усть прямая L проходит через точку в направлении вектора . Так как важно направление, а не точка приложения вектора , то его всегда можно отложить так, чтобы прямая проходила через него, например, поместив его начало в точку . Возьмем на прямой произвольную точку и соединим ее вектором с М₀. Тогда вектора – коллинеарны, т.к. лежат на одной прямой. Т.к. координаты коллинеарных векторов пропорциональны, то:

.

Параметрические уравнения прямой

Примем каждое из отношений в предыдущих уравнениях за параметр t, который может принимать любые значения, т.к. m, n, p – заданы, а координаты x, y, z могут принимать любые значения.

,

откуда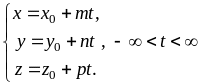

Наиболее часто параметром t является время.