Выполнение действий с векторами через их координаты
В координатной форме записи удобно выполнять любые действия с векторами.
Чтобы умножить вектор на число, нужно все его координаты умножить на это число:
.
Чтобы найти сумму или разность векторов, нужно сложить или вычесть соответствующие координаты.
;
;
;
.
Используя свойства скалярного произведения, а также тот факт, что базисные вектора взаимно ортогональны, можно получить формулу для вычисления скалярного произведения векторов, заданных своими координатами:
; ;
.
Скалярное произведение векторов равно сумме произведений соответствующих координат.
Формула для вычисления угла между векторами:
Учитывая свойства векторного произведения и взаимную перпендикулярность базисных векторов, можно получить способ определения координат векторного произведения через координаты входящих в него векторов и .
; ;
.
Формулы для вычисления координат векторного произведения легче запоминаются, если представить его в виде определителя, составленного из базисных векторов и координат векторов и , разложенного по элементам первой строки:
Смешанное произведение легко вычисляется, если вектора заданы своими координатами:
Смешанное произведение равно определителю, составленному из координат векторов, входящих в смешанное произведение.
2.2. Пример решения контрольной работы №2
Задание 1
Дано:
.
Для векторов
и
найти скалярное произведение и модуль
векторного произведения.
Решение
Используя свойства и определение скалярного произведения, найдём:
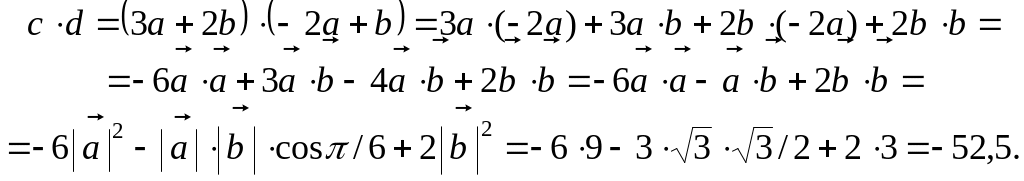
Используя свойства векторного произведения векторов и определение его модуля, найдём:
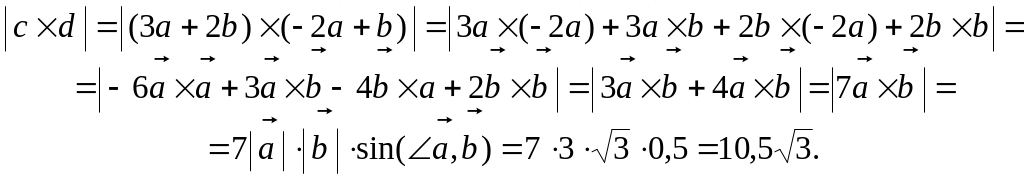
Задание 2
Дан тетраэдр с вершинами в точках
.
Найти: 1) внутренние углы в основании
(с точностью до десятых долей градуса),
сделать проверку;
2) объём пирамиды, площадь основания
и длину высоты, проведённой из вершины
.
Решение
1) Внутренние углы в основании
можно найти как углы между векторами,
выходящими из соответствующих вершин:
,
,
.
Как изложено в теоретическом материале, координаты вектора равны разности координат конца и начала вектора, его длина равна корню квадратному из суммы квадратов его координат. Тогда:
Подставим координаты векторов и их длины в формулы для нахождения косинусов углов:
;
;
.
Проверка:
.
С учётом проведённых округлений нахождение углов можно признать правильным.
2) Как показано в теоретическом материале данного раздела, объём треугольной пирамиды можно найти как 1/6 модуля смешанного произведения векторов, на которых она построена:
.
Найдём смешанное произведение векторов,
учитывая координаты вектора
:
.
Тогда
.
Площадь треугольника, являющегося основанием , можно найти как половину модуля векторного произведения векторов, которые образуют данный треугольник:
.
Найдём векторное произведение:
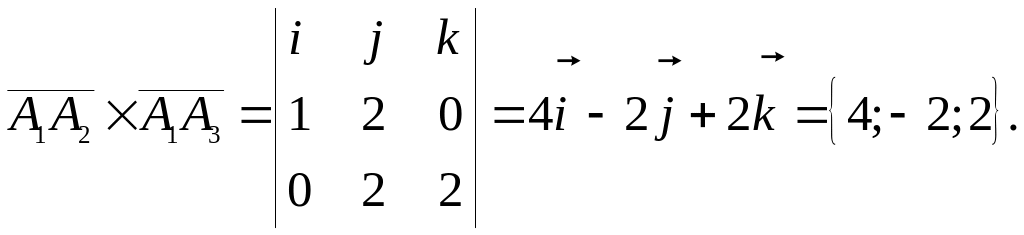
Тогда площадь основания
.
Высоту пирамиды из вершины
найдём, используя формулу:
.
В данном случае
и высота
.
Ответ: 1)
2)
;
;
.
2.3. Задания контрольной работы №2
Вариант 1
Задание 1
Дано:
.
Для векторов
и
найти скалярное произведение и модуль
векторного произведения.
Задание 2
Дан тетраэдр с вершинами в точках
.
Найти: 1) внутренние углы в основании (с точностью до десятых долей градуса), сделать проверку;
2) объём пирамиды, площадь основания и длину высоты, проведённой из вершины .
Вариант 2
Задание 1
Дано:
.
Для векторов
и
найти скалярное произведение и модуль
векторного произведения.
Задание 2
Дан тетраэдр с вершинами в точках
.
Найти: 1) внутренние углы в основании (с точностью до десятых долей градуса), сделать проверку;
2) объём пирамиды, площадь основания и длину высоты, проведённой из вершины .
Вариант 3
Задание 1
Дано:
.
Для векторов
и
найти скалярное произведение и модуль
векторного произведения.
Задание 2
Дан тетраэдр с вершинами в точках
.
Найти: 1) внутренние углы в основании (с точностью до десятых долей градуса), сделать проверку;
2) объём пирамиды, площадь основания и длину высоты, проведённой из вершины .
Вариант 4
Задание 1
Дано:
.
Для векторов
и
найти скалярное произведение и модуль
векторного произведения.
Задание 2
Дан тетраэдр с вершинами в точках
.
Найти: 1) внутренние углы в основании (с точностью до десятых долей градуса), сделать проверку;
2) объём пирамиды, площадь основания и длину высоты, проведённой из вершины .
Вариант 5
Задание 1
Дано:
.
Для векторов
и
найти скалярное произведение и модуль
векторного произведения.
Задание 2
Дан тетраэдр с вершинами в точках
.
Найти: 1) внутренние углы в основании (с точностью до десятых долей градуса), сделать проверку;
2) объём пирамиды, площадь основания и длину высоты, проведённой из вершины .
Вариант 6
Задание 1
Дано:
.
Для векторов
и
найти скалярное произведение и модуль
векторного произведения.
Задание 2
Дан тетраэдр с вершинами в точках
.
Найти: 1) внутренние углы в основании (с точностью до десятых долей градуса), сделать проверку;
2) объём пирамиды, площадь основания и длину высоты, проведённой из вершины .
Вариант 7
Задание 1
Дано:
.
Для векторов
и
найти скалярное произведение и модуль
векторного произведения.
Задание 2
Дан тетраэдр с вершинами в точках
.
Найти: 1) внутренние углы в основании (с точностью до десятых долей градуса), сделать проверку;
2) объём пирамиды, площадь основания и длину высоты, проведённой из вершины .
Вариант 8
Задание 1
Дано:
.
Для векторов
и
найти скалярное произведение и модуль
векторного произведения.
Задание 2
Дан тетраэдр с вершинами в точках
.
Найти: 1) внутренние углы в основании (с точностью до десятых долей градуса), сделать проверку;
2) объём пирамиды, площадь основания и длину высоты, проведённой из вершины .
Вариант 9
Задание 1
Дано:
.
Для векторов
и
найти скалярное произведение и модуль
векторного произведения.
Задание 2
Дан тетраэдр с вершинами в точках
.
Найти: 1) внутренние углы в основании (с точностью до десятых долей градуса), сделать проверку;
2) объём пирамиды, площадь основания и длину высоты, проведённой из вершины .
Вариант 10
Задание 1
Дано:
.
Для векторов
и
найти скалярное произведение и модуль
векторного произведения.
Задание 2
Дан тетраэдр с вершинами в точках
.
Найти: 1) внутренние углы в основании (с точностью до десятых долей градуса), сделать проверку;
2) объём пирамиды, площадь основания и длину высоты, проведённой из вершины .
Раздел 3. Контрольная работа по высшей математике №3
3.1. Теоретический материал по аналитической геометрии
3.1.1. Плоскость
Уравнением плоскости будем называть соотношение между декартовыми координатами x, y, z произвольной точки плоскости, которому удовлетворяют координаты любой точки, принадлежащей данной плоскости.
Уравнение плоскости, проходящей через данную точку, перпендикулярно данному вектору
Составим уравнение плоскости P,
проходящей через точку
,
перпендикулярно вектору
,
направленному от начала координат к
плоскости.
– произвольная точка плоскости P.
Рассмотрим вектор
.
По условию вектор
перпендикулярен плоскости Р,
следовательно, вектор
перпендикулярен вектору
(т.к.
лежит на плоскости Р) и их скалярное
произведение равно нулю, т.е.
,
или 
.
Общее уравнение плоскости
Раскроем скобки в полученном уравнении и приведем подобные члены:
.
Обозначив через
,
получим
.
Составленное уравнение называется
общим уравнением плоскости. Оно
является линейным алгебраическим
уравнением, коэффициенты при
,
и
дают координаты нормального (т.е.
перпендикулярного) вектора плоскости.
Уравнение плоскости в отрезках
Рассмотрим общее уравнение плоскости .
Перенесем слагаемое D
в правую сторону и разделим обе части
уравнения на
:
,
,
.
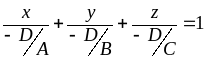Обозначим:
,
.
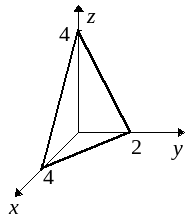
Это уравнение называется уравнением плоскости в отрезках, где a, b, c – отрезки (с учетом знаков), отсекаемые плоскостью на осях координат.
Пример. Построить плоскость
.
Перепишем уравнение в виде
.
Треугольник, изображенный на рисунке, соединяет точки, отсекаемые плоскостью на координатных осях. Этот треугольник является частью плоскости и показывает ее расположение в пространстве.