Гипербола

Гиперболой называется геометрическое место точек, для каждой из которых, модуль разности расстояний до двух фиксированных точек, называемых фокусами, имеет постоянное значение, меньшее расстояния между фокусами.

Если разместить фокусы гиперболы на симметрично началу координат в точках и , обозначить расстояния от произвольной точки на гиперболе до фокусов и , а модуль их разности положить равным , то можно выписать условие для составления уравнения гиперболы в декартовой системе координат:

Преобразуя выписанное равенство подобно тому, как это было сделано при выводе уравнения эллипса, получим каноническое уравнение гиперболы:

В уравнении использовано обозначение (поскольку ). Отношение называется эксцентриситетом гиперболы.

Если фокусы гиперболы расположить на , уравнение гиперболы будет иметь вид:

или

Такая гипербола называется сопряженной.

Для построения графика гиперболы, описываемой уравнением , отметим, что он должен проходить через точки и - вершины гиперболы, кроме этого график не может пересекать .

Учитывая этот результат, график гиперболы строим следующим образом. Проводим прямые и , эти линии ограничат основной прямоугольник гиперболы. Проведем прямые, совпадающие с диагоналями этого прямоугольника, это будут асимптоты гиперболы.

Отметим вершины и , затем проведем линии, плавно приближаясь от вершин к асимптотам.

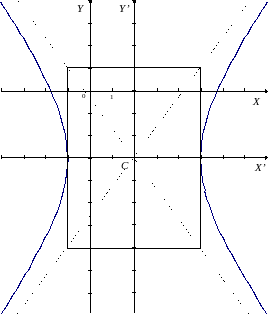
График гиперболы состоит из двух половин — ветвей, он имеет две оси симметрии и центр симметрии.

Пунктирной линией на рисунке нанесен график сопряженной гиперболы.

Уравнение гиперболы, центр симметрии которой находится в точке , а оси симметрии параллельны координатным осям, получается аналогично подобному уравнению для эллипса:

(**)

Отметим, что в уравнении гиперболы коэффициенты при и разных знаков.

Пример. Установить, что уравнение

определяет гиперболу и построить ее.

Т.к. коэффициенты при и разных знаков, то можно предположить, что это уравнение гиперболы. Чтобы убедиться в этом, преобразуем заданное уравнение к виду (**).

Сгруппируем слагаемые с и и вынесем имеющиеся при них общие множители за скобки:

.

Выделим в скобках полный квадрат:

;

;

;

.

Разделим обе части последнего равенства на 144: .

Это уравнение гиперболы с центром в и полуосями и .

Отметим положение центра и проведем через него вспомогательные оси и . Отложим вправо и влево от по 3 единицы и проведем прямые, параллельные оси , отложив вверх и вниз по 4 единицы, проведем прямые, параллельные оси . Прямые, совпадающие с диагоналями получившегося прямоугольника являются асимптотами нашей гиперболы, отметим ее вершины на и построим график.

Парабола

Параболой называется геометрическое место точек, равноудаленных от заданной точки, называемой фокусом, и заданной прямой, называемой директрисой при условии, что директриса не проходит через фокус.

Чтобы составить уравнение параболы, разместим фокус в точке , директрису проведем параллельно оси через точку . Расстояние от произвольной точки , принадлежащей параболе, до директрисы обозначим , а расстояние от до фокуса — . По определению ;

.

Возведем в квадрат обе части уравнения: .

Раскрывая скобки и приводя подобные, получим каноническое уравнение параболы:

.

Если , то ветви параболы направлены в сторону положительного направления оси , если , то в обратную.

Если расположить директрису параллельно , а фокус на оси , то получим уравнение параболы в виде:

В соответствии со знаком параметра ветви такой параболы будут смотреть вверх ( ) или вниз ( ).

График параболы имеет только одну ось симметрии и не имеет центра симметрии. На графике имеется точка, называемая вершиной параболы.

Если вершина параболы находится не в начале координат, а в произвольной точке , то уравнение параболы имеет вид:

или .

В уравнение параболы одна из координат входит в первой степени, а другая - во второй.