Введение

Данное пособие написано для того, чтобы помочь студентам, обучающимся на факультете заочного и дистанционного обучения по направлению «Электроэнергетика и электротехника» и профилю «электрооборудование и электрохозяйство предприятий, организаций и учреждений», в изучении линейной и векторной алгебры, аналитической геометрии, а также в выполнении контрольных работ по высшей математике по соответствующим темам: № 1, №2, №3.

В пособии содержатся три раздела, в каждом из которых имеется необходимый теоретический материал, пример выполнения соответствующей контрольной работы и задания для самостоятельного выполнения в десяти вариантах. Номер варианта определяется по последней цифре зачётной книжки (шифра).

Работу следует выполнять в тонкой ученической тетради в клетку. Выполненную работу следует снабдить титульным листом, образец которого можно найти на доске объявлений у деканата.

Поскольку пособие содержит достаточно большой теоретический материал, полезно сохранить его до конца обучения в вузе, так как он может быть востребован при дальнейшем изучении математики и других дисциплин.

Раздел 1. Контрольная работа по высшей математике №1

1.1. Теоретический материал по линейной алгебре

1.1.1. Комплексные числа и действия с ними

Под комплексным числом в алгебраической форме записи понимается выражение где и – действительные числа, а – мнимая единица, для которой справедлива формула

Числа вида отождествляются с действительными числами, числа вида называются чисто мнимыми. Сопряженным числом к числу называется комплексное число Два комплексных числа и равны, если и

Сложение, вычитание, умножение и деление комплексных чисел определяются следующим образом.

1)

2)

3)

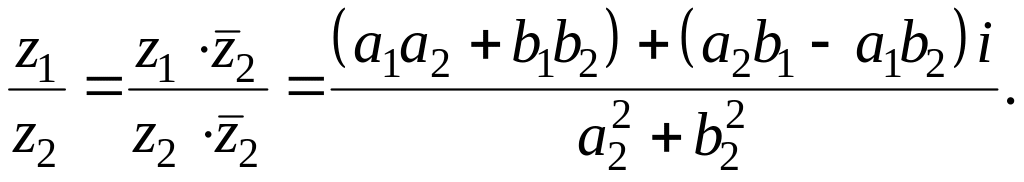
Примечание. Формулу умножения двух комплексных чисел не обязательно запоминать, так как она получается, если формально перемножить двучлены и по обычному правилу умножения двучленов и затем заменить на –1.

Примеры.

1. Найти сумму и произведение комплексных чисел и

Находим сумму:

Умножим:

2. Найти частное комплексных чисел и

Для нахождения частного умножим числитель и знаменатель дроби на число, сопряженное знаменателю:

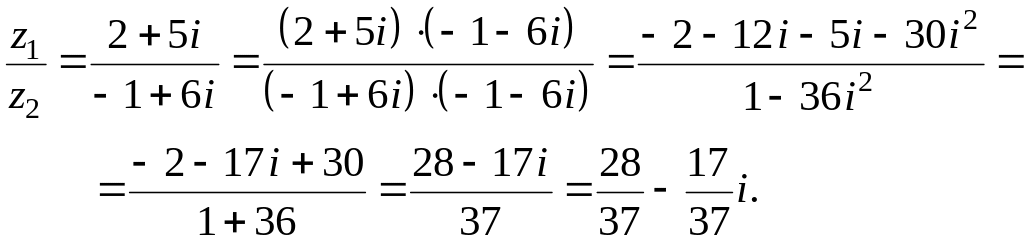
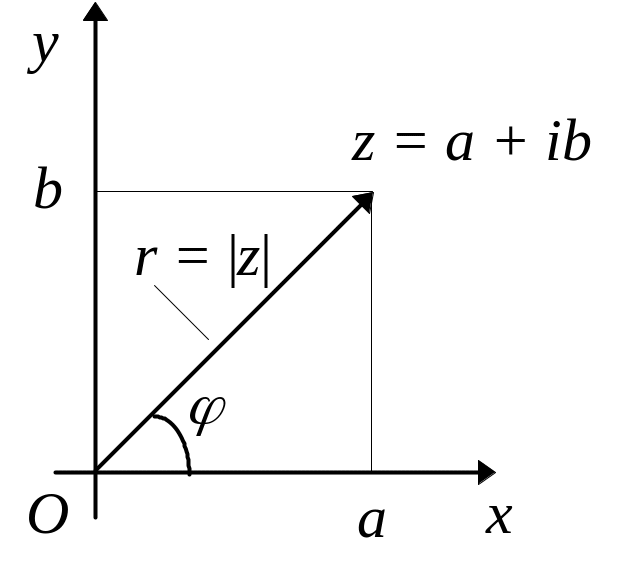
Комплексное число можно изобразить точкой на плоскости имеющей координаты На оси изображаются действительные числа, поэтому она называется действительной осью; на оси расположены чисто мнимые числа; она называется мнимой осью.

Можно также сопоставить числу вектор, направленный из начала координат в точку Длина этого вектора , т.е. расстояние от начала координат до точки называется модулем комплексного числа и обозначается

Из рисунка находим Следовательно:

Такая форма записи комплексного числа называется тригонометрической. Угол , образованный радиус-вектором с положительным направлением действительной оси называется аргументом комплексного числа и обозначается . В инженерных приложениях угол также называется фазой. Величина угла определяется с точностью до слагаемого Главным называется значение , удовлетворяющее условию: .

Главное значение аргумента можно вычислить по следующим формулам:

Пусть – любое действительное число. Символом обозначается комплексное число С помощью этого обозначения всякое комплексное число может быть записано в показательной форме (формула Эйлера):

Пример. Представить в тригонометрической и показательной форме комплексное число

Находим модуль Аргумент находим по формуле:

.

Следовательно