3. Доминирование стратегий игроков

Решение в матричных играх, особенно если матрица большая, получается путем громоздких вычислений и преобразований. Поэтому необходимо по возможности сократить матрицу и упростить решение, не в ущерб результату. В качестве такого сокращения используется понятие доминирования стратегий.

Решение матричной игры можно упростить, если своевременно выявить имеющееся в платежной матрице доминирование одних стратегий над другими, поскольку это позволит предварительно сократить размерность матрицы.

Иногда возможно упростить игры, применяя следующие принципы:

1. Игрок А стремится увеличить свой выигрыш, поэтому он не будет использовать стратегии, которые заведомо дают ему меньшие суммы. Необходимо оставить доминирующие стратегии и отбросить доминируемую стратегию – в платежной отбросить ту строку, элементы которой меньше соответствующих элементов другой строки.

2. Игрок В стремится уменьшить свой проигрыш, поэтому он не будет использовать стратегии, которые заведомо отнимают большие суммы. Необходимо оставить доминирующие стратегии и отбросить доминируемую стратегию – в платежной отбросить тот столбец, элементы которого больше соответствующих элементов другого столбца.

Пример 2. Выполнить возможные упрощения платежной матрицы

.

Проанализируем матрицу сначала с позиции игрока .

Элементы первой и третьей строк соответственно равны, поэтому одну из них (например, третью) можно отбросить. Элементы второй строки не превышают соответствующих элементов первой строки, поэтому вторую строку отбрасываем и приходим к матрице .

У игрока А остались доминирующие стратегии А₃ и А₄.

Проанализируем теперь полученную матрицу с позиции игрока .

Элементы первого столбца данной матрицы превышают соответствующие элементы второго столбца, элементы третьего – элементы четвертого, а элементы пятого – элементы второго столбца. Поэтому доминируемые первый, третий и пятый столбцы отбрасываем. В результате получаем матрицу . У игрока В остались доминирующие стратегии В₂ и В₄.

Вывод. Таким образом, если строка матрицы А доминируется какой-либо другой (то есть она меньше) строк, то ее можно вычеркнуть и решать задачу с меньшей матрицей, а решение исходной задачи получить добавив нули вместо недостающих координат в векторе первого игрока.

Если столбец матрицы А доминирует какой-либо другой (то есть он «больше» всех остальных столбцов), то его можно вычеркнуть, решить игру с меньшим количеством столбцов и получить оптимальные смешанные стратегии добавлением нулей вместо недостающих координат в векторе второго игрока.

4. Оптимальные смешанные стратегии лпр

Если матричная игра не имеет седловой точки (ситуации равновесия), то ее решение в чистых стратегиях становится непредсказуемым: каждому игроку можно только гарантировать, что его выигрыш при разумном поведении будет не менее нижней границы и не более верхней границы, цены игры.

Матричная игра без седловой точки приводит к неустойчивости использования стратегий при многократном повторении игры.

Если игра не имеет седловой точки, и применение чистых стратегий не дает оптимального решения игры. В этом случае можно получить оптимальное решение, случайным образом чередуя чистые стратегии.

• Смешанной стратегией игрока называется полный набор вероятностей применения его чистых стратегий: 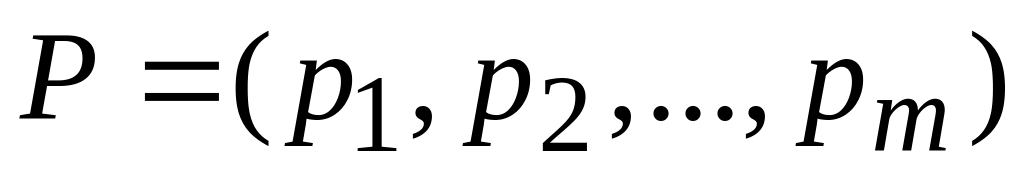, где , .

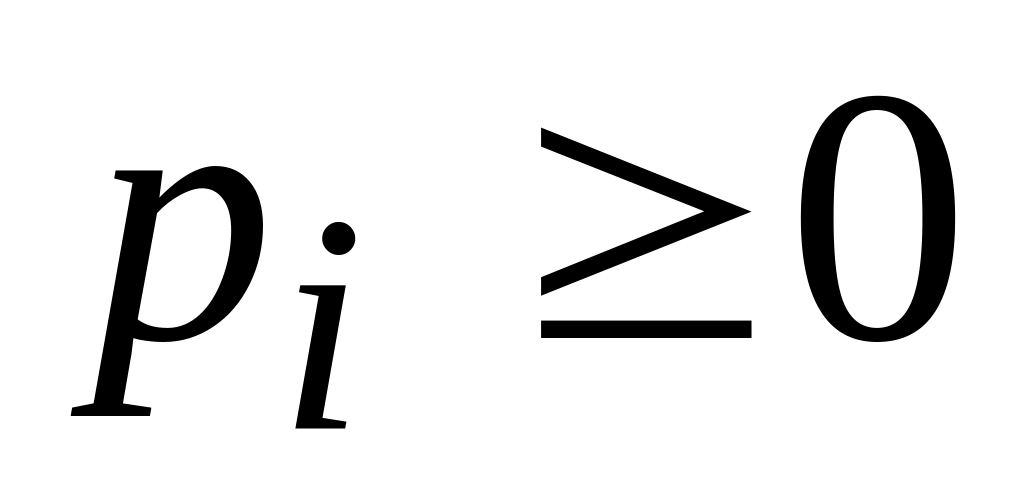• Смешанной стратегией игрока называется полный набор вероятностей применения его чистых стратегий: , где , .

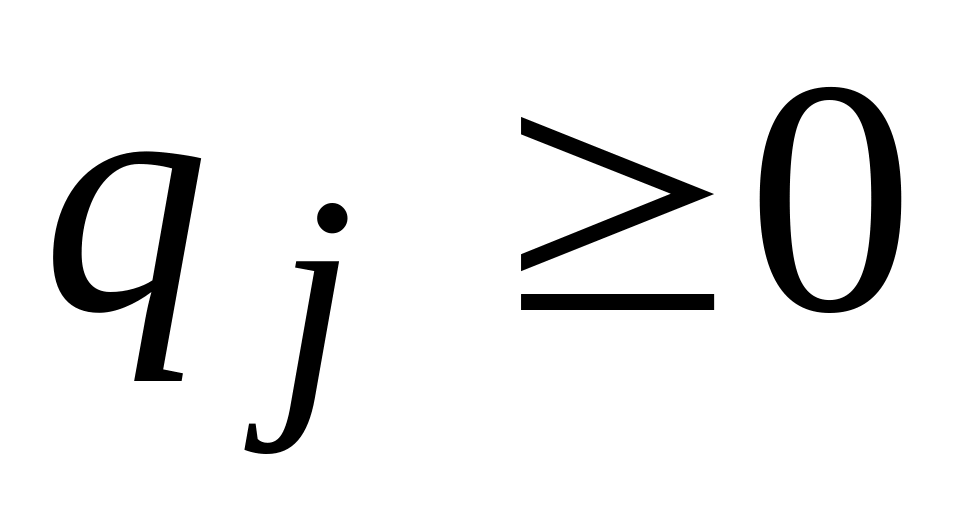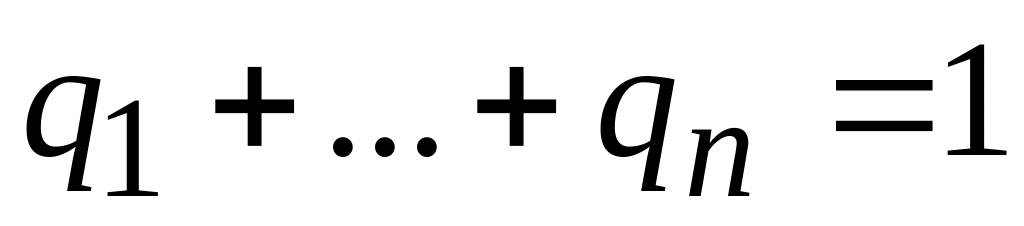Игра приобретает случайный характер, поэтому является случайной и величина выигрыша игрока (проигрыша игрока ). Значит, можно вести речь о средней величине (математическом ожидании) выигрыша (проигрыша).

Для платежной матрицы и смешанных стратегиях и средняя величина выигрыша (математическое ожидание) примет вид

.