2.2. Определение скорости при координатном способе задания движения точки

На основании выражений (8) и (2)

. (9)

В свою очередь вектор скорости, в заданный момент времени, также можно представить через проекции скоростей на единичные вектора координатных осей,

. (10)

С

Рис.4.

равнивая уравнения (9) и (10), получаем

, , . (11)

Таким образом, проекции скорости точки на координатные оси представляют собой первые производные от соответствующих координат движущейся точки по времени.

Зная проекции вектора скорости на оси координат, определим модуль скорости и косинусы углов с осями координат (рис.4)

, (12)

. (13)

2.3. Определение скорости при естественном способе задания движения точки

При естественном способе известны траектория и закон движения точки S=f(t).

В выражении (8), где радиус-вектор однозначно определяет положение движущейся точки М в векторной форме в декартовой системе координат; положение же точки при естественном способе задается законом S=f(t), тогда справедливо равенство

. (14)

Вектор скорости в данный момент времени есть первая производная по времени от закона движущейся точки.

В случае если при нахождении скорости в заданный момент времени, численное значение окажется больше нуля (V 0), то скорость направлена по касательной к траектории в сторону положительного отсчета расстояния S. При V 0 – скорость направлена по касательной к траектории в сторону отрицательного отсчета расстояния S.

2.4. Ускорение точки

Ускорение точки – векторная величина, характеризующая изменение ее скорости с течением времени.

П

Рис.5.

усть в некоторый момент времени t движущаяся точка находится в положении М и обладает скоростью , а в момент t₁ приходит в положение М₁, со скоростью (рис.5).

Вектором среднего ускорения точки за промежуток времени называется отношение векторного приращения скорости к промежутку времени

. (15)

Направление вектора среднего ускорения совпадает с направлением вектора приращения скорости .

Ускорение точки в данный момент времени представляет собой вектор численно равный отношению вектора приращения скорости к промежутку времени , при

. (16)

С учетом уравнения (8)

. (17)

Вектор ускорения точки в данный момент времени 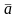лежит в плоскости, по которой происходит бесконечно малое перемещение движущейся точки, направленный в сторону вогнутости кривой.

Ускорение точки в данный момент времени – вектор равный первой производной от вектора скорости по времени или второй производной от радиус-вектора движущейся точки по времени.

2.5. Определение ускорения точки при координатном способе задания движения точки

На основании выражений (17) и (2)

. (18)

В свою очередь, вектор ускорения в заданный момент времени также можно представить через проекции ускорений на единичные вектора координатных осей,

. (19)

Сравнивая уравнения (18) и (19), с учетом (11) получаем

, , . (20)

Т аким образом, проекции ускорения точки на координатные оси представляют собой первые производные от проекций скорости или вторые производные от соответствующих координат движущейся точки по времени.

З

Рис.6.

ная проекции вектора ускорения на оси координат, определим модуль ускорения в заданный момент времени и косинусы углов с осями координат (рис.6)

, (21)

. (22)