Практическое занятие 5

Тема занятия: Одномерные модели временных рядов

Интерактивная форма проведения занятия

Занятие проводится в форме кресельного кейс-метода. Условие задачи содержит реальный практический смысл. Поэтому преподаватель предлагает выполнить комплекс эконометрических расчетов, идентифицировать и верифицировать результаты с целью их экономической интерпретации. На первом этапе преподаватель объявляет группы из двух-трех магистрантов для совместного выполнения практического задания. Роль преподавателя на данном этапе заключается в постоянном поддержании активного внутригруппового взаимодействия, снятии напряженности во взаимоотношениях между участниками, оперативном вмешательстве в случае возникновения непредвиденных трудностей, а также в целях пояснения новых положений учебной программы. На втором этапе преподаватель назначает лидера для руководства ходом обсуждения результатов выполнения задания. Лидер, применяя уникальное сочетание компьютерных и традиционных методов организации учебной деятельности демонстрирует основные формулы, используемые в решении задания. Совместно с преподавателем лидер руководит групповым обсуждением области применения формул, полученных эконометрических оценок и их качества, экономической интерпретацией результатов. Преподаватель побуждает магистрантов к обоснованию в аудитории полученных результатов, конструктивной критике и поддержке выводов одногруппников с целью формирования навыков изучения реальных социально-экономических явлений и процессов, проблемных ситуаций, высказывания и отстаивания собственной точки зрения, концентрируя внимание на следующих вопросах:

1. Виды моделей регрессии для временных рядов.

2. Тренд-сезонные модели временных рядов. Автокорреляция уровней ряда.

3. Ложная регрессия в моделях временных рядов.

В конце занятия преподаватель подводит итоги и оценивает каждого студента в зависимости от его участия в выполнении заданий и обсуждении вопросов.

Расчетные формулы

Компоненты динамического ряда позволяют представить уровень динамического ряда в виде аддитивной или мультипликативной моделей:

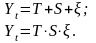
Если амплитуда сезонных колебаний постоянна, то применяется аддитивная модель. Если амплитуда колебаний изменяется во времени, то рассматривается мультипликативная модель.

Построение тренд-сезонных моделей временных рядов сводится к расчету значений Т, S или Е для каждого уровня ряда. Процесс построения модели включает в себя следующие этапы:

1. Выравнивание исходного ряда методом скользящей средней.

2. Расчет значений сезонной компоненты S.

3. Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных (Т+Е) в аддитивной или (Т*Е) в мультипликативной модели.

4. Аналитическое выравнивание уровней (Т+Е) или (Т*Е) и расчет значений Т с использованием полученного уравнения тренда.

5. Расчет полученных по модели значений (Т+S) или (Т*S)

6. Расчет абсолютных и относительных ошибок.

Применение трендовых временных рядов в качестве зависимой и объясняющих переменных имеет важную особенность. Пусть Y_t=α₀+α₁*t+u_t,

X_t=γ₀+γ₁*t+v_t и оценивается линейная модель регрессии

Y_t=β₀+β₁*x_t+e. Тогда невключение значимого фактора времени (t) приводит к смещению OLS –оценок параметров регрессии, в частности, коэффициент β₁ может оказаться значимым, хотя из экономических соображений факторы должны быть независимыми. Описанная проблема называется ложной регрессией. Необходимо учесть тренд (включить в модель значимый фактор времени) и оценивать регрессию Y_t=β₀+β₁*x_t+β₂*t+e.