Практическое занятие 3
Тема занятия: Модели бинарного выбора: логит-модель, пробит-модель
Расчетные формулы
В моделях бинарного выбора зависимые переменные являются двоичными.
Модель для двоичной переменной имеет вид
-
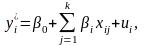
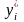скрытая (латентная) переменная,
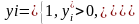
Представленная модель называется моделью вероятности. Часто на практике используется логитовая модель вида:
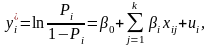
где называется логитом, а Pi определяется вероятностью зависимой переменной Yt, рассчитываемой на основе логистического распределения:
В пробитовой модели, по аналогии с логитовой моделью, ненаблюдаемая величина Pi рассчитывается исходя из дистрибуанты нормального распределения как:
Параметры логитовой и пробитовой моделей связаны соотношением:
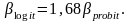
На практике может использоваться любой из этих методов, поскольку все меры соответствия моделей эмпирическим данным оказываются для них идентичными.
Логитовый анализ используется в экономических исследованиях применительно к срезам индивидуальных данных тогда, когда эндогенная переменная имеет двоичный характер. Чаще всего эта переменная представляет результаты принятия рациональных экономических решений, например, приобретения автомобиля или квартиры, предоставления банковского кредита, слияния или поглощения фирм.
Задание для выполнения в аудитории
Задание 3.1. Фирма «Бэст Перспектива» заключила договор с ОАО «Центртелеком», предметом которого является оказание услуг связи, в том числе и доступ в Интернет. С целью увеличения интеллектуального потенциала фирмы руководство решило расширить круг своих сотрудников, обладающих правом бесплатного доступа. Выбор таких сотрудников решено было осуществлять с учетом ряда факторов, тем или иным образом характеризующих претендентов с точки зрения эффективного использования Интернет-ресурсов. В связи с эти возник вопрос: Кому из претендентов на бесплатный доступ предоставить такую возможность в первую очередь? Для того, чтобы получить обоснованный ответ, руководство фирмы поручило экономико-аналитическому отделу разработать модель, позволяющую по каждому претенденту рассчитать прогнозную оценку целесообразности предоставления ему права бесплатного доступа к ресурсам Интернета. В основу построения такой модели была положена идея применения бинарной переменной Y: Y=1, если сотрудник, обладающий правом бесплатного доступа к Интернет-ресурсам, по оценке экспертной группы, эффективно пользуется эти правом; Y=0, в противном случае. Построение модели руководство фирмы предложило провести по пяти факторам: возраст (X1, лет), стаж профессиональной деятельности (X2, лет), заработная плата (X3, тыс. ден. ед.), число случаев поступления полезной для фирмы информации от сотрудника (X4, ед.), результат тестирования на предмет оценки навыков работы в Интернет (X5, в баллах). Значения этих показателей, а также значения бинарной переменной для 100 сотрудников фирмы представлены в таблице.
Таблица 3.1
№ |
Y |
X1 |
X2 |
X3 |
X4 |
X5 |
№ |
Y |
X1 |
X2 |
X3 |
X4 |
X5 |
1 |
0 |
22 |
1 |
2,5 |
2 |
6 |
51 |
0 |
57 |
18 |
10,2 |
2 |
2 |
2 |
0 |
24 |
1 |
3 |
3 |
8 |
52 |
0 |
28 |
4 |
6,7 |
1 |
11 |
3 |
1 |
25 |
1 |
2,1 |
1 |
7 |
53 |
0 |
52 |
14 |
9,9 |
2 |
2 |
4 |
1 |
27 |
4 |
4,6 |
8 |
11 |
54 |
0 |
45 |
15 |
13,1 |
3 |
4 |
5 |
1 |
28 |
3 |
5,9 |
9 |
13 |
55 |
0 |
53 |
16 |
9,1 |
1 |
4 |
6 |
0 |
21 |
1 |
3,3 |
5 |
14 |
56 |
0 |
54 |
20 |
9,7 |
1 |
5 |
7 |
1 |
22 |
1 |
3,2 |
9 |
15 |
57 |
0 |
30 |
4 |
6,8 |
3 |
12 |
8 |
0 |
29 |
5 |
6 |
1 |
13 |
58 |
0 |
46 |
12 |
12,2 |
2 |
1 |
9 |
1 |
26 |
4 |
2,7 |
8 |
11 |
59 |
0 |
28 |
4 |
3,9 |
0 |
2 |
10 |
0 |
27 |
6 |
3,8 |
0 |
3 |
60 |
0 |
44 |
14 |
12,5 |
1 |
2 |
11 |
1 |
28 |
4 |
4,2 |
9 |
11 |
61 |
0 |
22 |
1 |
2,8 |
3 |
7 |
12 |
0 |
29 |
3 |
6,7 |
5 |
13 |
62 |
0 |
29 |
4 |
3,4 |
0 |
2 |
13 |
1 |
29 |
9 |
6,5 |
10 |
14 |
63 |
0 |
23 |
1 |
4,9 |
4 |
15 |
14 |
1 |
30 |
4 |
3,4 |
9 |
13 |
64 |
1 |
26 |
8 |
6,7 |
12 |
15 |
15 |
1 |
41 |
7 |
7,2 |
7 |
15 |
65 |
1 |
27 |
9 |
6,6 |
11 |
13 |
16 |
0 |
32 |
8 |
7,9 |
4 |
7 |
66 |
0 |
39 |
4 |
8,9 |
2 |
8 |
17 |
1 |
46 |
9 |
6,4 |
9 |
12 |
67 |
1 |
27 |
7 |
5,5 |
11 |
11 |
18 |
1 |
34 |
3 |
6,3 |
8 |
13 |
68 |
0 |
26 |
6 |
5,7 |
2 |
11 |
19 |
0 |
33 |
3 |
6,1 |
1 |
9 |
69 |
1 |
28 |
9 |
6,1 |
12 |
12 |
20 |
1 |
47 |
9 |
9,7 |
5 |
13 |
70 |
1 |
28 |
8 |
7,3 |
10 |
13 |
21 |
0 |
37 |
2 |
6,4 |
3 |
7 |
71 |
0 |
40 |
4 |
9,2 |
2 |
7 |
22 |
0 |
38 |
5 |
10,5 |
2 |
8 |
72 |
1 |
28 |
10 |
7,9 |
10 |
11 |
23 |
0 |
49 |
13 |
12,3 |
3 |
3 |
73 |
1 |
22 |
1 |
2,5 |
8 |
12 |
24 |
1 |
46 |
7 |
10,1 |
5 |
14 |
74 |
1 |
26 |
9 |
6,8 |
11 |
5 |
25 |
1 |
48 |
8 |
7,9 |
8 |
15 |
75 |
0 |
40 |
5 |
6 |
2 |
9 |
26 |
0 |
52 |
17 |
9,7 |
2 |
1 |
76 |
1 |
26 |
8 |
5,4 |
11 |
15 |
27 |
0 |
54 |
12 |
8,9 |
3 |
4 |
77 |
0 |
39 |
5 |
7,6 |
2 |
7 |
28 |
1 |
18 |
1 |
3,4 |
4 |
11 |
78 |
0 |
32 |
9 |
5,5 |
5 |
8 |
29 |
0 |
19 |
1 |
3,7 |
5 |
12 |
79 |
1 |
33 |
4 |
5,4 |
7 |
11 |
30 |
1 |
20 |
1 |
2,9 |
6 |
13 |
80 |
1 |
23 |
1 |
2,8 |
8 |
13 |
31 |
0 |
19 |
1 |
3,8 |
5 |
15 |
81 |
0 |
36 |
3 |
6,5 |
2 |
9 |
32 |
0 |
20 |
1 |
4,3 |
1 |
8 |
82 |
0 |
35 |
9 |
6,9 |
5 |
8 |
33 |
1 |
28 |
2 |
6,9 |
9 |
14 |
83 |
1 |
23 |
1 |
3,2 |
9 |
11 |
34 |
0 |
27 |
4 |
6,5 |
5 |
12 |
84 |
1 |
34 |
3 |
6,1 |
8 |
12 |
35 |
0 |
43 |
8 |
9,2 |
2 |
9 |
85 |
0 |
35 |
8 |
5,9 |
5 |
9 |
36 |
1 |
44 |
13 |
10,3 |
11 |
13 |
86 |
0 |
38 |
2 |
7,8 |
3 |
10 |
37 |
0 |
56 |
12 |
10,8 |
2 |
4 |
87 |
0 |
32 |
9 |
7,3 |
5 |
8 |
38 |
1 |
54 |
14 |
9,4 |
12 |
13 |
88 |
0 |
33 |
2 |
6,4 |
3 |
10 |
39 |
0 |
44 |
11 |
9,8 |
2 |
6 |
89 |
1 |
34 |
3 |
6,5 |
8 |
11 |
40 |
1 |
28 |
4 |
6 |
8 |
12 |
90 |
0 |
35 |
10 |
7,9 |
5 |
10 |
41 |
0 |
19 |
1 |
3,4 |
2 |
7 |
91 |
0 |
33 |
2 |
7,8 |
1 |
9 |
42 |
0 |
20 |
1 |
4,3 |
5 |
11 |
92 |
1 |
24 |
1 |
3 |
8 |
11 |
43 |
0 |
19 |
1 |
4,9 |
5 |
12 |
93 |
1 |
34 |
4 |
6 |
9 |
13 |
44 |
1 |
21 |
1 |
3,2 |
6 |
13 |
94 |
0 |
33 |
3 |
5,4 |
2 |
10 |
45 |
0 |
45 |
12 |
12,4 |
2 |
4 |
95 |
1 |
22 |
1 |
2,9 |
7 |
13 |
46 |
0 |
19 |
1 |
3,1 |
4 |
13 |
96 |
1 |
32 |
5 |
6,4 |
8 |
15 |
47 |
0 |
48 |
13 |
12,7 |
2 |
5 |
97 |
0 |
33 |
6 |
5,7 |
2 |
7 |
48 |
1 |
20 |
1 |
3,5 |
4 |
13 |
98 |
1 |
23 |
1 |
3,6 |
9 |
15 |
49 |
0 |
58 |
18 |
9,9 |
2 |
2 |
99 |
1 |
31 |
4 |
6 |
8 |
13 |
50 |
0 |
49 |
12 |
11,8 |
3 |
3 |
100 |
0 |
33 |
4 |
6,1 |
3 |
10 |
Имеются следующие претенденты на право бесплатного доступа.
1) возраст – 27 лет, стаж – 3 года, заработная плата – 3200 руб., количество случаев нахождения полезной для фирмы информации – 9 раз, тест – 15 баллов;
2) возраст – 44 года, стаж – 12 лет, заработная плата – 5600 руб., количество случаев нахождения полезной для фирмы информации – 2 раза, тест – 5 баллов;
3) возраст – 35 лет, стаж – 10 лет, заработная плата – 4100 руб., количество случаев нахождения полезной для фирмы информации – 4 раза, тест – 7 баллов;
4) возраст – 39 лет, стаж – 13 лет, заработная плата – 7500 руб., количество случаев нахождения полезной для фирмы информации – 11 раз, тест – 15 баллов.
Используя построенную прогнозную модель, определить среди имеющихся претендентов тех, кому в первую очередь следует предоставить право бесплатного доступа к ресурсам Интернета.