3. Плоскопараллельное движение

Плоскопараллельное движение – это такой вид движения, при котором точки абсолютно твердого тела движутся в плоскостях, параллельных друг другу.

Многие звенья машин и механизмов совершают такое движение. например, качение колеса по прямолинейному рельсу, движение шатуна в кривошипно-ползунном механизме и т.д.

Закон плоскопараллельного движения

Точки тела, лежащие на одном перпендикуляре к неподвижной плоскости H, имеют одинаковые траектории, скорости и ускорения, так как этот перпендикуляр движется поступательно. Следовательно, для изучения движений точек этого перпендикуляра, достаточно изучить движение одной из них, например М (см. рис.2.17), а значит, для изучения движения плоскопараллельного движения тела, достаточно изучить движение точек тела, лежащих в сечении тела плоскостью П , параллельной неподвижной плоскости H, т.е. движение плоской фигуры S.

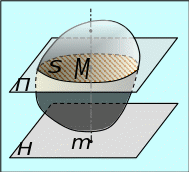
Рис.2.17

Положение фигуры S в плоскости П определяется положением любого отрезка АМ (рис. 2.18), принадлежащего фигуре. В свою очередь, положение отрезка АМ задается координатами одной из его точек, например А, которую называют полюсом, и ориентационным углом отрезка АМ.

Рис. 2.18

  Таким образом, для описания положение тела надо задать закон плоскопараллельного движения (или иногда говорят "плоского движения") в виде функций:

, либо ,

(2.53)

при этом функции и описывают поступательное движение фигуры S вместе с полюсом А, функция - вращение фигуры вокруг полюса.

Отсюда следует, что плоскопараллельное движение можно рассматривать как совокупность (сумму) поступательного движения, при котором все точки тела движутся так же, как полюс А, и вращения тела вокруг оси, проходящей через этот полюс.

Скорости точек тела при плоском движении

 

Определение скоростей через полюс

Если в качестве полюса выбрать точку А, для любой другой точки тела (например, т. В) можно записать:

.

Продифференцируем это выражение по времени:

,

или

,

(2.54)

где ` – скорость произвольной точки В тела, – скорость полюса,` – скорость точки В при вращении (тела) вокруг полюса A (читается: «скорость В относительно А», либо «скорость В при её вращении вокруг А»).

Скорость движения точки В относительно полюса А определим по формуле для вращательного движения (2.40):

= ω∙АВ.

(2.55)

Естественно, вектор ` направлен перпендикулярно отрезку АВ в сторону вращения тела (см. рис. 2.18).

Таким образом, вектор скорости ( ) произвольной точки В тела при плоскопараллельном движении равен геометрической сумме векторов скорости полюса ( ) и скорости вращения точки ( ) относительно полюса.

Р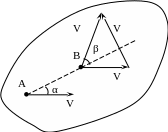 ис. 2.19

Иллюстрацией такой формулировки служит рисунок 2.19, где векторное сложение выполнено по правилу треугольника, и рисунок 2.21, где сложение выполнено по правилу параллелограмма.

Определение скоростей через мгновенный центр скоростей (м.ц.с.)

Мгновенный центр скоростей - точка P плоской фигуры, скорость `V_P которой в данный момент времени равна нулю(V_P =0).

Пусть такая точка существует. Тогда выражение (2.54) для точки P будет иметь вид:

.

При `V<sub>P</sub> = 0 должно быть: , откуда . Поскольку V<sub>Р/А</sub>= w×AP и` перпендикулярен отрезку AP, то мгновенный центр скоростей (м.ц.с.) будет находиться на перпендикуляре к и на расстоянии АР, равном:

.

(2.56)

Найдя такую точку и приняв ее за полюс, выражение (2.54) для произвольной точки С примет вид: . Поскольку V_P = 0, то окончательно: , а ее модуль равен:

.

(2.57)

_{Формально отсюда следует, что скорость точки С и скорость движения (вращения) т. С относительно т. Р – одно и то же.}

Следовательно, скорости точек тела определяются, как если бы оно вращалось вокруг оси, проходящей через мгновенный центр скоростей (рис. 2.20). При этом скорости точек тела и расстояния от них до м.ц.с. определяется следующими соотношениями:

.

(2.58)

Рис. 2.20 

Для определения положения мгновенного центра скоростей знать линии по которым направлены скорости двух любых точек А и В. М.ц.с. будет находиться на пересечении перпендикуляров к этим линиям. Для определения направления вращения фигуры необходимо знать направление вектора скорости одной из точек А или В. И, наконец, для определения величин скоростей других точек, согласно выражению (2.58), необходимо знать величину скорости одной из точек А или В.

Так, например, при качении без проскальзывания колеса точка касания является мгновенным центром скоростей.

Определение скоростей по теореме о проекциях скоростей двух точек

Е сли спроецировать на прямую АВ скорости точек А и В (рис. 2.21, 2.22), определяемые векторным соотношением (2.54), то в силу перпендикулярности вектора отрезку АВ его проекция будет равна нулю.

Рис.2.21

Рис.2.22

Тогда после проецирования выражение (2.54) приобретет вид:

= , или .

(2.59)

Сформулируем соответствующий вывод:

Проекции скоростей двух точек абсолютно твердого тела на прямую, проходящую через эти точки, равны.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Что такое мгновенный центр скоростей? Как найти его местоположение?

2. Приведите формулировки трех рассмотренных приемов по определению скоростей точек тела при его плоскопараллельном движении.

3. Подумайте, как найти местоположение мгновенного центра скоростей в случае, если точки А, В и Р (рис.2.20) лежат на одной прямой?

Ускорения точек тела при плоском движении

Определение ускорений через полюс

Продифференцируем выражение (2.54) по времени:

_.

_{Каждое из членов этого равенства представляет собой соответствующее ускорение, которое может быть записано кратко, в виде полного ускорения, так и в развернутом виде, через свои касательные и нормальные компоненты:}

(2.60)

Вектор ускорения ( ) произвольной точки В тела при плоскопараллельном движении равен геометрической сумме векторов ускорения полюса ( ) и полного ускорения ( ) точки при ее вращении относительно полюса.

Следует отметить, касательные и нормальные направления в (2.60) каждого полного ускорения различаются, поскольку траектории движения точек А и В вообще говоря разные, а траектория движения т. В относительно т. А – окружность радиуса АВ. Поэтому нормальный вектор направлен из т. В в т. А вдоль ВА, а касательный вектор перпендикулярен АВ и направлен в сторону углового ускорения тела.

Иллюстрацией соотношений между векторами по (2.60) служит рис.2.23.

Рис. 2.23

Определение ускорений через мгновенный центр ускорений (м.ц.у.)

Мгновенный центр ускорений - точка Q плоской фигуры, ускорение ` которой в данный момент времени равна нулю( =0).

Используя подход, аналогичный примененному при рассмотрении мгновенного центра скоростей, можно так сформулировать основные результаты:

• Мгновенный центр ускорений находится на пересечении прямых, проведенных к векторам ускорений точек абсолютно твердого тела под углами μ в направление углового ускорения ε (рис.2.24) ( ).

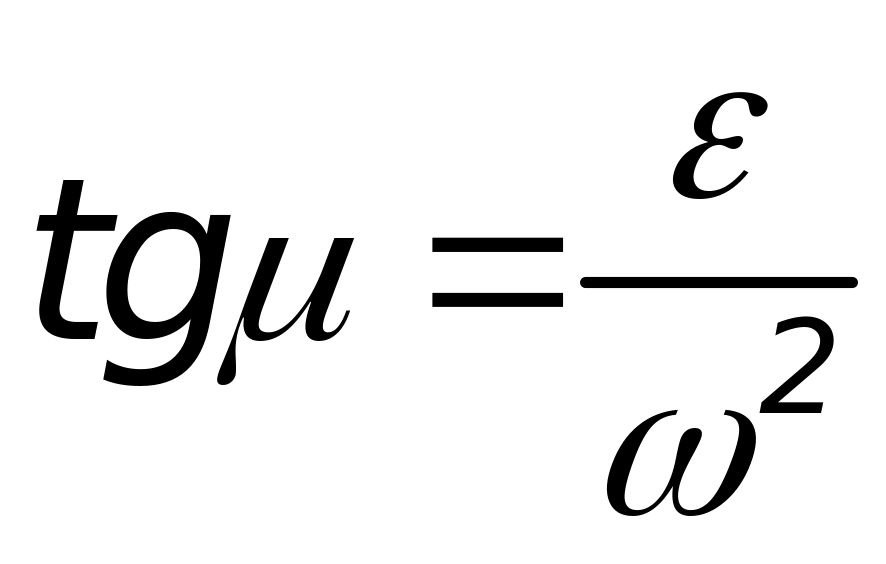• Ускорения точек тела определяются, как если бы оно вращалось вокруг оси, проходящей через мгновенный центр ускорений (т. Q, рис. 2.24). При этом ускорения точек тела и расстояния от них до м.ц.у. определяется следующими соотношениями:

.

(2.60)

Рис.2.24

Замечание

Мгновенный центр ускорений (м.ц.у.) и мгновенный центр скоростей (м.ц.с.) – вообще говоря, разные точки. Они могут совпадать в отдельных случаях, например, при вращательном движении вокруг неподвижной оси.

Так, в случае равномерного качении колеса без проскальзывания мгновенный центр скоростей (м.ц.с.) - это точка касания колеса опорной поверхности. Мгновенный же центр ускорений (м.ц.у.) – точка, совпадающая с движущимся центром колеса.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Что такое мгновенный центр ускорений? Как найти его местоположение?

2. Сформулируйте методы определения ускорений точек тела при плоскопараллельном движении.

3. Подумайте, как найти местоположение мгновенного центра ускорений в случае, если точки А, В и Q (рис.2.24) лежат на одной прямой?