Изучение движения тела переменной массы (ракета)

Принадлежности : 1) установка, 2) секундомер.

Теория. Цель задачи - изучение движения тела, движущегося подобно ракете.

Установка, применяющаяся при этом, изображена схематически на рис.1. Она состоит из двух полых цилиндров А и В равного веса и объема, которые висят на нити, перекинутой через блок С .

Цилиндр В имеет одно отверстие в середине дна. Цилиндр А имеет два одинаковых отверстия в боковой поверхности. Оба цилиндра могут наполняться водой. Отверстия в цилиндрах подобраны так, что масса воды, вытекающей в единицу времени, одинакова для обоих цилиндров.

С начала истечения воды к цилиндру В будет приложена реактивная сила, направленная вверх, которая и приведет систему в движение.

Величина реактивной силы Ф определяется относительной скоростью истечения воды и и скоростью изменения массы цилиндра (воды)

:

Ф = . (1)

Уравнение движения для цилиндра В (считаем нить нерастяжимой, пренебрегаем ее массой и силой трения) может быть написано в виде

m mg , (2)

где m - масса цилиндра ( с водой) в любой момент времени после начала движения, Т- натяжение нити, g - ускорение силы тяжести.

Уравнение движения для цилиндра А ( при тех же условиях) имеет вид

- m mg. (3)

Из уравнений (2) и (3) получаем

2m или 2 .

Интегрирование при u= const дает

2 .

Определяя константу интегрирования из условия, что при t = 0 v =0, m = m_{0 ,}

получаем

. (4)

Это уравнение отличается от “ уравнения Циолковского” только наличием дополнительного множителя 2 в показателе степени.

Движение цилиндра В , следовательно, аналогично движению ракеты вне поля тяготения. Упростим это уравнение. Если v<u, то

. ¹⁾ (5)

Правую часть уравнения (4) можно написать в виде ,

где m₀ - масса цилиндра ( с водой) при t = 0 , m - то же в момент времени t , m₁ - масса воды, вытекшая за время t.

Если m₁ << m₀ масса m₁ = - m₀

. ²⁾ (6)

Из уравнений (4), (5) и (6) получим

. (7)

При m₁ << m₀ масса m₁ = ( = const). Это дает

V = .

Для расстояния s, проходимого цилиндром В за время t , получаем (по модулю)

S = . (8)

Эта формула может быть экспериментально проверена измерением s и t.

Описание установки. Цилиндры А и В (рис.2) равного веса и объема из стекла висят на нити, перекинутой через легкий блок С, который укреплен на стене. Для отсчета уровня воды в цилиндрах на каждом из них ( в верхней части) нанесена шкала. Над цилиндрами имеются диски D ( назначение их будет ясно из дальнейшего).

Ниже блока С к вертикальной доске прикреплен прозрачный короб Е с открытым верхом. Дно короба может откидываться рычагом Р . Когда цилиндры висят примерно на одном уровне, то они находятся внутри короба. Ниже первого короба на доске прикреплен второй короб G с прозрачной передней стенкой и открытым верхом ( подвижное дно первого короба движется в верхней части второго короба.

Цилиндры наполняются водой сверху через две трубки К , соединенные гибким резиновым шлангом с краном водопровода. Трубки могут передвигаться в горизонтальном направлении. Передвижение их осуществляется с помощью рычагов (неуказанных на рисунке) тем же рычагом Р . Когда дно короба не откинуто ( находится в горизонтальном положении), концы трубок, подающих воду, находятся над цилиндрами и струи воды наполняют их. Излишек воды сливается через края цилиндров в нижний короб.

Поворотом рычага Р трубки отодвигаются, т.е. прекращается поступление воды в цилиндры ( вода из трубок сливается в нижний короб) и одновременно открывается дно короба. При этом освобождается цилиндр А и начинается движение цилиндров.

Расстояние, проходимое цилиндром В , определяется по шкале L и может быть заранее задано благодаря платформе M , которая может перемещаться по стержню N и закрепляться на нем. При движении цилиндров платформа, сквозь которую проходит нить, не пропускает диска D - движение прекращается. Стопор S - плоская металлическая пластинка, конец которой подводится под диск D цилиндра А , - не позволяет системе двигаться.

Для удаления воды из нижнего короба служит трубка, соединенная со стоком раковины водопровода. Трубка эта расположена несколько выше дна короба, поэтому в коробе всегда имеется вода, играющая роль амортизатора : цилиндр А , двигаясь вниз, останавливается, погружаясь в воду.

При выполнении работы следует быть осторожным, не закрывать дна короба до тех пор, пока оба цилидра не будут подняты выше плоскости дна, не пускать сильных струй воды резким поворотом крана водопровода. При передвижении цилиндров руками это необходимо делать осторожно, чтобы не выдернуть нити из углубления блока.

Следует следить за тем, как бьют струи из отверстий цилиндров, и в случае их засорения сообщить об этом лаборанту.

Измерения. Для измерений необходимы два человека. Прежде всего определяют величину . Для этого закрепляют стопором S цилиндры и после наполнения их водой отодвигают рычагом Р дно сосуда, пуская одновременно в ход секундомер. Через 4, 5, 10, 13, 15 сек отсчитывают положение опускающегося уровня воды в цилиндре В ( один работающий делает отсчет по секундомеру, другой по шкале на цилиндре В).

Строят график, по горизонтальной оси которого отложено время, а по вертикальной - количество вытекающей воды ( диаметры цилиндров известны, плотность воды принимается равной единице).

Через точки, нанесенные на миллиметровой бумаге, проводится линия, проходящая через начало координат. При малых значениях времени истечения эта линия будет прямой, тангенс угла наклона ее к оси времени и дает величину .

Необходимо убедиться, что имеет одно и то же численное значение для обоих цилиндров. Только в этом случае возможно дальнейшее проведение работы.

Убедившись в этом, закрывают дно короба ( цилиндры должны быть

при этом выше плоскости дна) и осторожно опускают цилиндр А на дно короба. Цилиндр А должен опираться о дно короба и находиться в вертикальном положении, цилиндр В должен быть при этом выше цилиндра А на 1-2 см.

Осторожно открывают кран водопровода и следят за наполнением цилиндров. Вода из цилиндров будет вытекать через отверстия, необходимо чтобы струи воды были в состоянии наполнить оба цилиндра, несмотря на утечку. Струи воды не должны быть, однако, очень сильными - это приведет к раскачиванию цилиндров, что совершенно недопустимо. Убедившись, что оба цилиндра наполнены водой и она переливается через края ( должны быть видны выпуклые мениски у обоих цилиндров), поворотом рычага Р откидывают дно короба и одновременно с этим пускают в ход секундомер. В момент удара диска о кольцо секундомер останавливают.

Измерения производят, располагая платформу так, чтобы проходимые расстояния составляли 75-100 см. Для каждого расстояния время движения определяют три раза и находят его среднее значение. Отношение пройденного расстояния ( определяемого по шкале) к квадрату среднего значения времени должно быть постоянной величиной для всех расстояний, т.е. должно выполняться соотношение

. (9)

Определяют величину среднего значения этих отношений К. Удвоенное значение этой величины является ускорением движения цилиндров.

a = 2К = . (10)

Величина скорости истечения воды определяется по формуле

u = (11)

где h - средняя (арифметическая) высота уровня воды в цилиндре за время движения, g - ускорение силы тяжести, - коэффициент скорости. Для определения величины h поступают так. Зная время движения цилиндров, определяют по графику высоту столба вытекшей воды за это время. Разность между полной высотой цилиндра ( она известна) и половиной высоты столба вытекшей воды дает величину h . Коэффициент скорости для случая отверстия в тонкой пластинке может быть принят ( по гидравлическим данным) равным 0,97 ;

g = 981 см/сек² .

Зная величины u и , вычисляют величину реактивной силы по формуле Ф = u . Зная m₀ , определяют величину этой силы по формуле

Ф = 4Km₀ .

Численные значения реактивной силы, полученные двумя способами, должны ( в пределах погрешности измерений) совпадать. Так как при движении цилиндров соблюдаются условия а << g и v << u , это позволяет :

1) величину , измеренную для неподвижных цилиндров, использовать при их движении, 2) скорость, определенную по формуле (11) , считать за относительную скорость истечения воды.

О коэффициенте полезного действия ракеты

Давайте начнем с рассмотрения задачи: за какое время электрический утюг потребляет столько энергии, сколько необходимо для его запуска на орбиту спутника Земли? ( Мощность утюга Р­ = 1 кВт, масса m = 1 кг )

Кинетическая энергия спутника, движущегося по круговой орбите, mv²/2 = mgR/2, где v - первая космическая скорость, R - радиус Земли. По определению первой космической скорости, высота h полета спутника равна нулю и поэтому потенциальной энергией mgh для не слишком высоких орбит можно пренебречь по сравнению с кинетической. Приравния энергию утюга-спутника к Pt, найдём, что t = mgR/(2P) = 3,2.10⁴ c » 9 ч.

Всего 9 часов! 9 киловатт-часов, 0,72 USD необходимы для выведения на орбиту спутника Земли каждого килограмма массы. Почему же для осуществления космических полетов требуются затраты, соизмеримые с национальными бюджетами небольших стран?

Потому, что эта энергия, 9 кВт-ч, необходима, но недостаточна. Дело в том, что ракета как тепловая машина имеет очень низкий коэффициент полезного действия. Попробуем его найти.

Сначала выведем формулу, связывающую массу и скорость ракеты, то есть решим «задачу Циолковского». Сложность здесь состоит в том, что масса ракеты при разгоне все время непрерывно уменьшается, поскольку выгорает топливо. Такие процессы изучают, решая дифференциальные уравнения.

Попытаемся обойтись без этого. Для простоты представим себе, что сгорание топлива происходит не непрерывно, а некими малыми порциями. Скажем, каждый раз ракета выбрасывает 1/N-ю часть своей массы, как бы выстреливает снарядом, масса которого в N раз меньше массы ракеты в этот момент ( рис. 1 ).

Скорость такого «снаряда» относительно ракеты будем считать постоянной и называть скоростью истечения V . При каждом таком «выстреле» выполняется закон сохранения количества движения. Пусть в начале масса ракеты была M₀, а скорость равна нулю. Тогда M₀V/N - количество движения (импульс) массы, выброшенной после первого толчка и (1–1/N)M₀v₁ - равный ему импульс ракеты. Итак, M₁ = M₀ (1 – 1/N), v₁ = V/N – 1.

После второго «выстрела» масса ракеты станет M₂ = M₁(1 – 1/N) = M₀(1 – 1/N)². Закон сохранения импульса, записанный в системе отсчета, связанной с ракетой, летящей со скоростью v₁, дает M₁V/N = M₂(v₂ – v₁) , и, таким образом, v₂ = v₁ + V(M₁/NM²) = 2V/(N -1).

После k-го «выстрела», как нетрудно видеть, скорость ракеты станет u_k = kV/N-1, а оставшееся масса M_k = M₀ (1 – 1/N)^k. Если нам нужно достичь скорости v, то необходимо сделать k = v/V(N – 1) «выстрелов», и оставшееся (полезная) масса будет равна m = M_k = M₀ í(1-1/N)^N-1ý ^v,V.

Реальный процесс истечения, как указывалось, происходит непрерывно. Это значит, что для того, чтобы рассмотренное нами движение хорошо описывало происходящее на самом деле, нам нужно брать как можно большие числа N , тогда движение ракеты будет состоять из большого числа маленьких по величине толчков, то есть будет почти непрерывным. Оказывается, что при увеличении N величина (1-1/N)^N стремится к конечному пределу. Этот предел равен 0,36788…. и обозначается в математике через е^-1, где е = 2,71828 - основание натуральных логарифмов.

Таким образом, масса ракеты, достигшей скорости v равна

m = M₀e^-v/V,

т.е. уменьшается с увеличением v по экспоненте.

Эта формула была получена К.Э. Циолковским в 1903 году и носит его имя. Из неё видно, что ракета может достичь скорости v, большей скорости истечения топлива V, но при этом её оставшаяся масса будет много меньше начальной, т.к. экспонента очень быстро убывает при возрастании v/V.

Если, например, скорость истечения равна 2 км/с, то при достижении первой космической скорости 7,9 км/с конечная масса будет в е^3,9 = 52 раза меньше начальной, а при достижении второй космической скорости 11,2 км/с – в е^5,6 = 270 раз меньше той же начальной массы. При этом надо иметь в виду, что значительная часть оставшейся массы приходится на конструкцию ракеты, так что доля действительно полезного груза становится ещё меньше. Чтобы уменьшить бесполезную массу, разгоняемую до конечной скорости, ракеты делают многоступенчатыми. При этом корпуса низших ступеней сбрасываются, когда в них кончается горючее. К.Э.Циолковский предлагал их сжигать.

Формулу Циолковского можно записать по-другому: v = V ln M₀ /m.

Отсюда следует, что для получения больших скоростей движения ракеты при заданных m и М₀ нужно максимально увеличить скорость истечения V. Однако для ракет, использующих энергию, выделяющуюся в результате химической реакции, то есть химических ракет, невозможно сделать скорость истечения больше некоторой величины, предельной для каждой реакции. И в этом нетрудно убедиться.

Пусть q – теплотворная способность данного топлива, то есть энергия, выделяющаяся при сгорании 1 кг его. Эта энергия расходуется на нагревание отходящих газов и на сообщение им кинетической энергии.

Рассмотрим ракетный двигатель, закреплённый неподвижно, так называемый стендовый двигатель. При сгорании массы m (мы считаем вместе и горючее, и окислитель) выделяется энергия qm, но только часть превращается в кинетическую энергию продуктов реакции mV²/2 .

Поэтому V²/2 < q. Если ввести коэффициент полезного действия стендового двигателя n₀ - отношение полезной *) энергии к затраченной, - то получим:

mV²/2 = η₀qm, V = 2 η ₀q,

то есть скорость истечения для данной химической реакции не может превысить её предельной скорости истечения V₀ = 2q (так как η ₀< 1 ).

*)Заметим, что энергия mV²/2 не является по-настоящему полезной. Ведь основная задача – разогнать до нужной скорости полезную массу, а не отходяшие газы.

Рассмотрим несколько химических реакций и вычислим для них предельные скорости истечения.

1. Горение ацетилена:

2С₂Н₂ + 5О = 4СО₂ + 2Н₂О + 611 ккал.

Число килокалорий в правой части уравнения реакции показывает, какая энергия выделяется при сгорании массы, равной сумме молей горючего и окислителя. В данном случае – при сгорании двух молей С₂Н₂ и пяти молей О₂, то есть всего 2 . 26 = 5 . 32 = 212 г. Таким образом, теплотворная способность этого топлива

q = 611 ккал/212 г = 2880 ккал/кг = 1,2 . 10⁷ м²/с²

а предельная скорость истечения V₀ = (2q)^1/2 = 4,9 км/с

2. 2H₂O + O₂ = 2H₂O_(газ) + 115,6 ккал

Вычисляем аналогично

q = 3220 ккал/кг; V₀ = 5,2 км/с

3. 2Al + 3/2O₂ = Al₂O₃ = 394 ккал; q = 3860 ккал/кг V₀ = 5,6 км/с

4. Наибольшая из всех возможных предельная скорость истечения достигается в реакции горения металлического бериллия:

Be + 1/2 O₂ = BeO + 146 ккал; q = 5840 ккал/кг; V₀ = 7 км/с

Практическому использованию этой реакции, однако, мешает то обстоятельство, что металлический бериллий и его соединения очень ядовиты.

5. Запишем для примера реакцию горения этилового спирта.

6. Для реакции горения керосина в кислороде имеем:

Рассмотрим теперь коэффициент полезного действия ракеты в целом, который определим как отношение кинетической энергии полезного груза, равной mv²/2, к затраченной. Последнюю, с небольшой ошибкой, можно считать равной qМ₀ , поскольку подавляющая часть начальной массы приходится на топливо. Таким образом,

η = mv²/2M₀q = v²/2q . e^-v/V

Или, подставляем вместо q его выражение из формулы V² = 2 η₀q, получаем η = η₀(v/V)² . e^-v/V

График зависимости n от v/V дан на рисунке 2.

Итак, только часть затраченной энергии, равная η qM₀ , превращается в кинетическую энергию ракеты.

Возникает вопрос, куда девается остальная часть затраченной энергии, поскольку в тепло при сгорании топлива переходит лишь (1 – η₀)qM₀ ответ состоит в том, что остальная энергия, а именно

(1 – η ₀)qM₀ - (1 – η ₀)qM₀ = (η ₀ – η)qM₀ = η ₀[1 – (v/V)²e^-v/V] qM₀

является кинетической энергией отходящих газов ракеты (в системе отсчёта Земли), которая в конечном счёте также переходит в тепло, нагревая атмосферу.

Таким образом, мы видим, что при достижении ракетой скорости, заметно большей скорости истечения, реальный коэффициент полезного действия становиться весьма малым. Например, если ракета со скоростью истечения v = 2 км/с достигает второй космической скорости v = 11,2 км/с, то η = 0,116 η₀ и, соответственно, 0,884 η₀ полной энергии ракеты уносят отходящие газы.

Создание мощных двигателей с большими скоростями истечения, использующих энергию ядерной реакции или разгон ионов в электрическом поле, существенно повысит к.п.д. ракет. Уже созданы плазменные двигатели, применяющиеся для маневрирования в космосе.

§

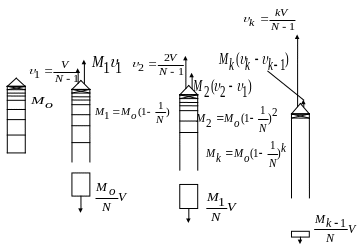
Параметры одноступенчатой тяжелой ракеты Blue Streak (Лазурная полоса)

Масса жидкого кислорода	61 500 кг
Масса керосина	26 500 кг
Масса конструкции	6 200 кг
Масса полезного груза	10 500 кг
Полная масса	104 700 кг
Удельный импульс	254 с
Тяга каждого из двух двигателей	621 400 Н
Время горения топлива	180 с
Скорость истечения газов	2,49 км/с
Теплотворная способность керосина	10 ккал/г
КПД сжигания топлива	0,3
Мощность двигателей суммарная	2 500 000 л.с.*
Температура горения	3 460 К
Средняя молярная масса отбрасываемых газов	31
Высота, до которой расходуется половина топлива	16 км

*1 л.с. = 0,735 кВт

Ракеты известны достаточно давно, само же слово «ракета» происходит от итальянского «веретенце».

Для осады крепостей в Китае и Индии (10 - 12 в.в.) уже применялись стрелы с бумажной гильзой, наполненной составом близким к пороху. В 1232 г. во время осады монголами китайского города Пиенг-Кинг осажденный гарнизон применил «огненные стрелы», вызвавшие пожары на больших территориях. В конце 18 в. ракеты с железными гильзами массой 3 – 6 кг с дальностью действия 1,5 – 2,5 км применялись индийскими войсками против англичан при осаде Серингапала. После англо-индийской войны ракетами заинтересовались в Европе. В 1807 г. в результате обстрела Копенгагнена англичанами сгорела большая часть этого города после выпуска 25 тыс. ракет массой от 6 до 20 кг и дальностью действия около 3 км (У. Конгрев). В начале 19 в. наблюдается расцвет ракетного оружия, но к концу 19 в. прогресс в нарезной артиллерии вытеснил ракеты. Возрождение ракетной техники в 20 – 30-ые годы 20 в. обусловлено применением малогабаритных жидкостных двигателей и их охлаждения самим топливом.

Реакция горения этилового спирта

С₂ Н₅ ОН + 3О₂ = 2СО₂ + 3Н₂ О + 328 ккал (137, 104 кДж)

Теоретическая скорость истечения газов – 4,4 км/с; реальная скорость истечения – 2,5 км/с, поскольку только часть химической энергии топлива преобразуется в кинетическую энергию газов.

Задача состоит в том, чтобы как можно больше энергии топлива переходило в механическую энергию. Этот максимум достигается, если процесс горения протекает адиабатически. Уравнение адиабаты имеет вид

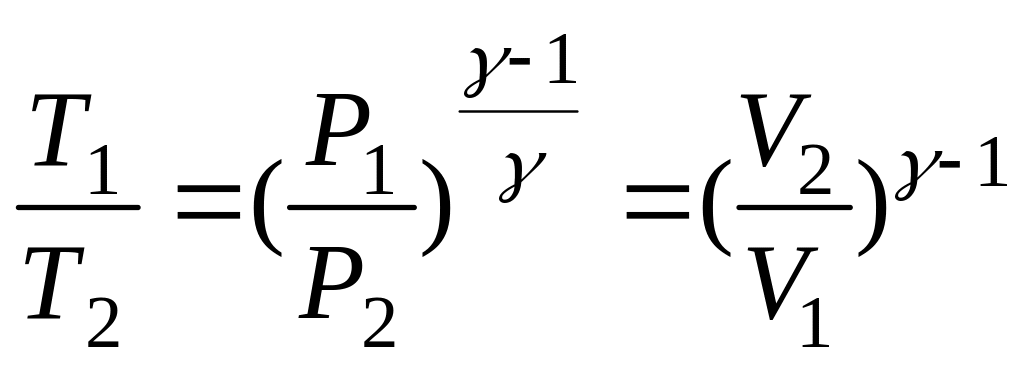
Определим механическую работу, совершаемую расширяющимися газами в сопле.

Сила, действующая на элемент газа в сопле F = S dp. Здесь S - площадь сечения сопла, ρ - плотность газа, dp – изменение давления по длине сопла.

Масса газа равна m = ρS dl. Здесь dl. – элемент длины сопла. Если скорость течения газа v, то dl = v dt, dt – время прохождения этого элемента длины частицами газа.

Ускорение α элемента газа будет равно , а сила F = ma. Из этих равенств имеем

S dp = ρS v dt , или dp = ρ v dv.

Интегрируя по всей длине сопла, имеем ∫dр/ ρ = (v₂² – v₀⁰)/2.

Здесь v₀ – скорость газа в камере сгорания, которая много меньше скорости v₂ в выходном сечении сопла.

Из уравнения адиабаты pv^γ = c имеем ρ₀ = ρ (р₀/р)^1/γ.

После интегрирования имеем

v₂ = =

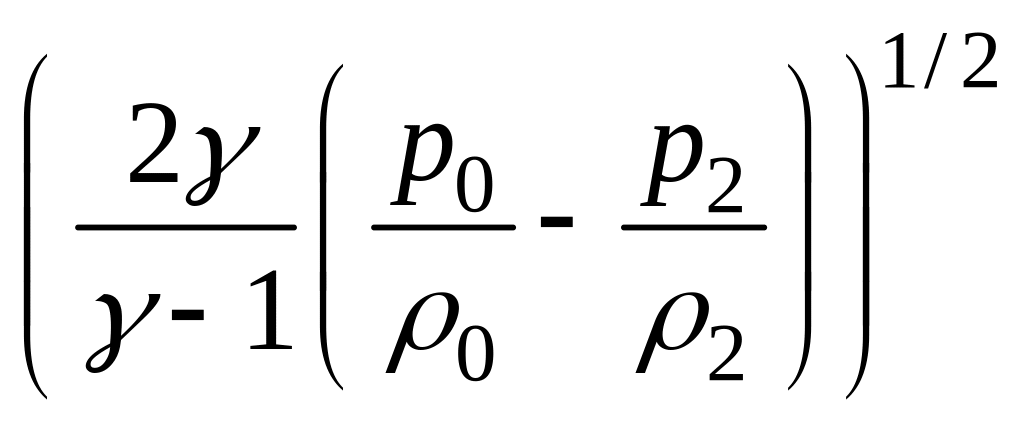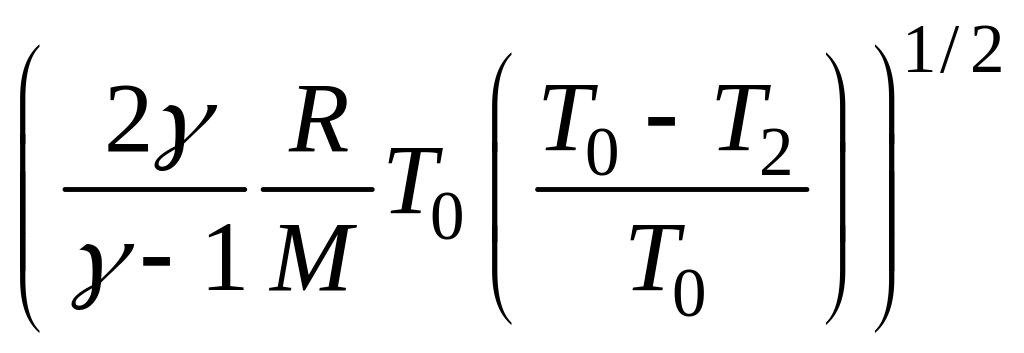
Здесь отношение η = (Т₀ – Т₂) / Т₀ – тепловой кпд идеальной тепловой машины.

Фактические значения кпд η₁ приведены в таблице

Отношение давлений р2/р1	η1	Отношение давлений р2/р1	η1	Отношение давлений р2/р	η1
1	0,091	0,1	0,380	0,02	0,525
0,5	0,190	0,05	0,448	0,01	0,577
0,2	0,304

Реальные кпд могут быть еще меньше в силу ряда причин:

- газ в ракетном двигателе не является идеальным;

- не учтены тепловые потери через стенки сопла во время расширения газа, на самом деле они равны примерно 3 %

- происходит трение газа о стенки сопла, а само сгорание не является полным; по этим причинам скорость истечения уменьшается на 5 % от теоретического значения;

- форма сопла не точно следует закону расширения газа, поток газа отрывается от стенок сопла и действительная степень расширения оказывается меньше расчетной;

- тягу создает только поток газа, отбрасываемого строго назад; при истечении из сопла скорость частиц составляет небольшой угол с осью расширяющегося сопла;

- продукты сгорания вследствие высокой температуры диссоциируют, что сопровождается поглощением энергии, например, при нормальном давлении и температуре 2000 ⁰С диссоциирует 1,5% СО₂ на СО и О₂, а при температуре 3000 ⁰С – 44 %;

- как видно из таблицы, кпд существенно зависит от внешнего давления, но двигатель рассчитывается для определенного давления и сопло работает в расчетном режиме всего лишь на небольшом участке подъема.

Для выведения массы m на орбиту высотой h над поверхностью Земли необходимо совершить работу А₁ по преодолению гравитационного поля и работу А₂ по приданию скорости v этой массе. Имеем

А = А₁ + А₂ = GM₃ m 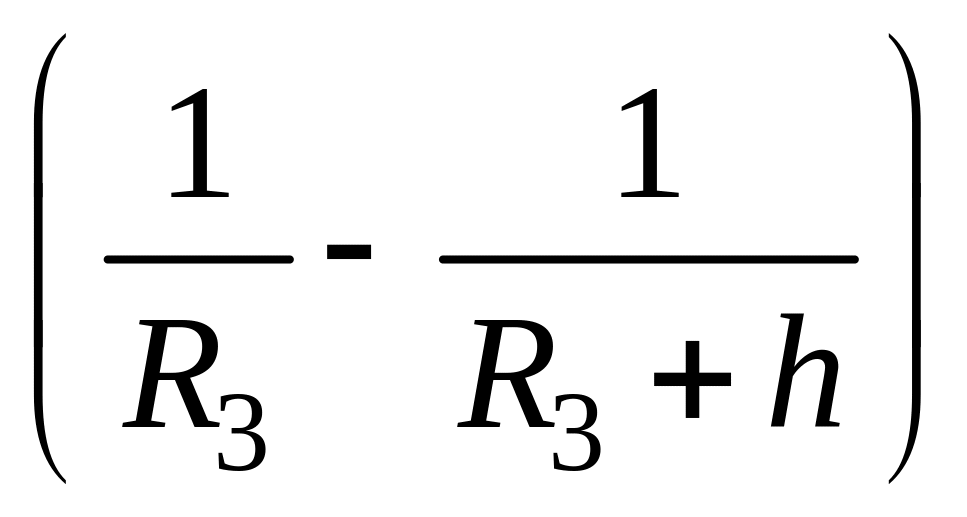+ mv²/2.

Здесь G – гравитационная постоянная, M₃ – масса Земли, R₃ – радиус Земли. Используем уравнение движения тела по круговой орбите

;

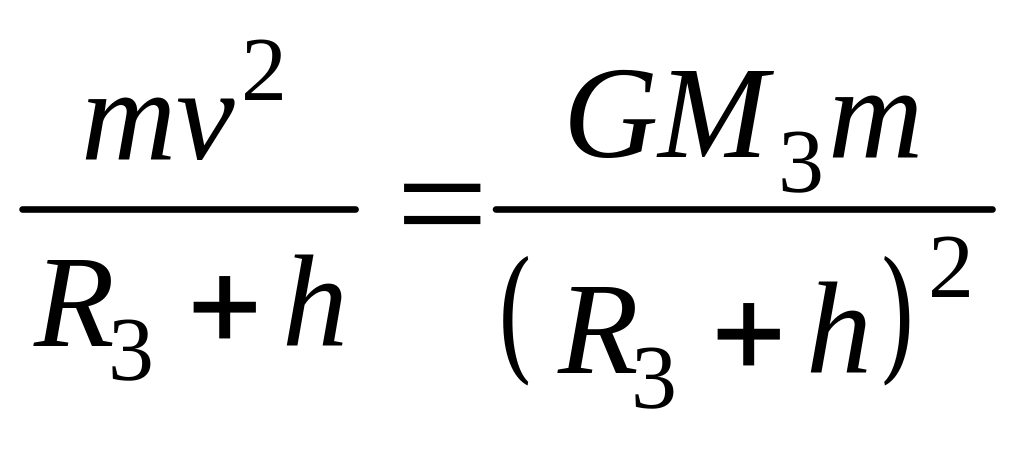с другой стороны на поверхности Земли сила тяжести mg равна силе гравитационного взаимодействия

; т.е. GM₃ = gR₃².

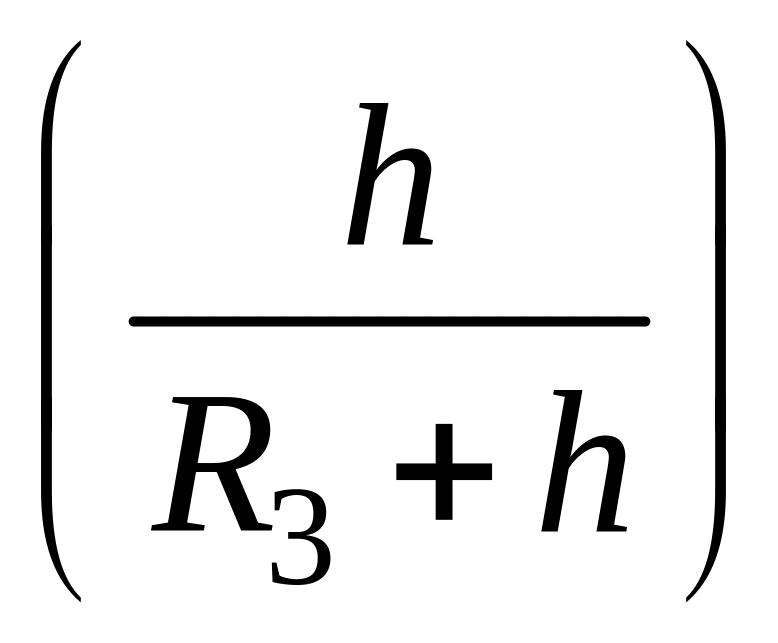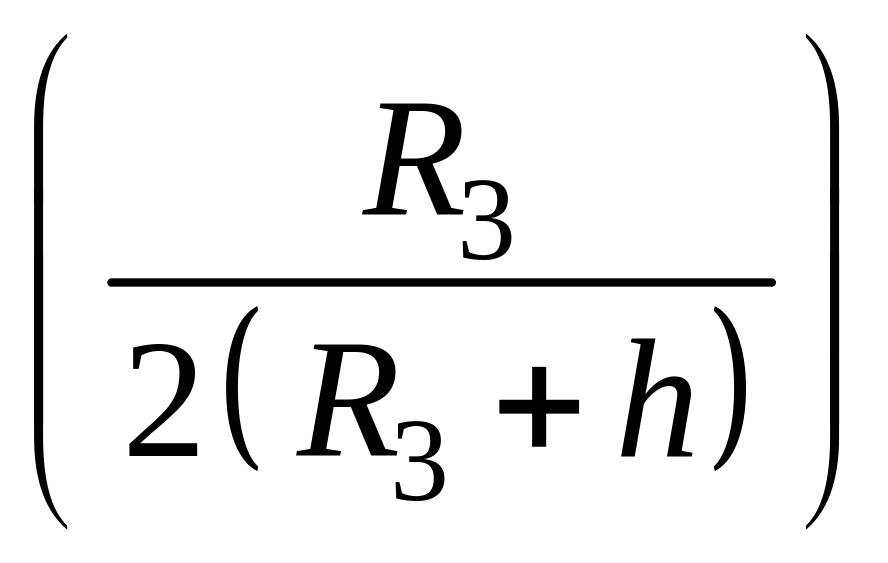Отсюда А₁ – работа в гравитационном поле равна gR₃m , а кинетическая энергия А₂ = gR₃m . Как видно, для малых высот h << R₃ имеем А₁ << А₂ . Полная работа по выводу спутника на круговую орбиту

А = gR₃m .

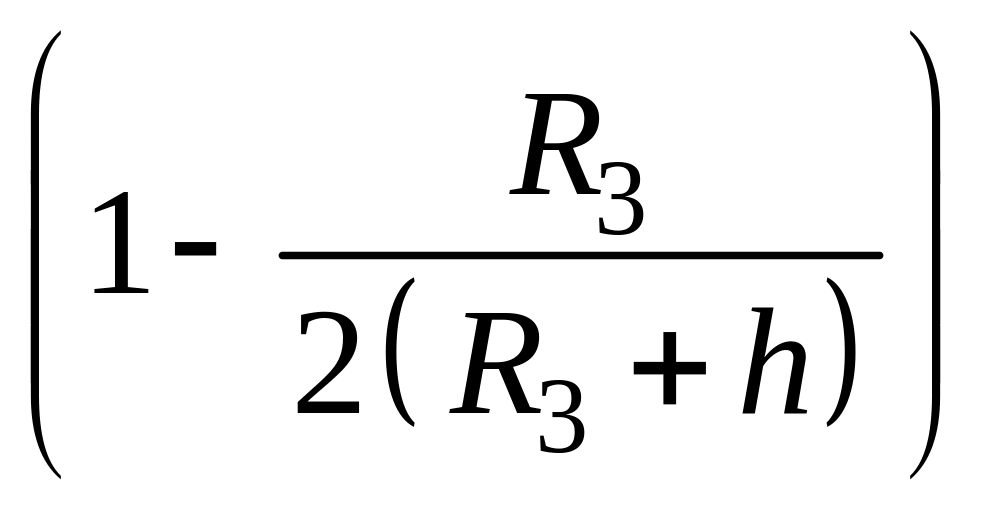Подставляя в эти соотношения массу m = 1 кг, получим, что для вывода ее на орбиту необходимо 33,44.10³ кДж = 8000 ккал. Но 1 кг топлива (горючее + окислитель) дает 10,241.10³ кДж = 2450 ккал, следовательно, для вывода необходимо только 3,25 кг горючего. Однако реально требуется не менее 88 кг горючего.

Идеальным топливом мог бы быть водород, но не сжигаемый стандартным способом. Если бы удалось накапливать атомарный водород, то при рекомбинации двух атомов в молекулу выделялась бы огромная энергия – 51,7 ккал на 1 г водорода. Поскольку молярная масса М = 2 г/моль, то при этом скорость истечения составила бы 18 км/с. Температура этого процесса около 12 000 К.

Много усилий прилагалось для создания ракеты на реакции деления ядер урана. В простейшем варианте жидкий водород впрыскивается в активную зону реактора, где нагревается до 3300 К и в дальнейшем истекает через сопло. При расходе водорода 257 кг/с и скорости истечения 8,9 км/с при нормальном внешнем давлении обеспечивается сила тяги 2 280 кН. Ракета смогла бы выводить массу в 18 т на орбиту спутника при полной массе 114 т.

В 1954 г Эрнст Штулингер предложил новый тип ракетного двигателя – ионного. Ионы цезия или рубидия образуются при испарении и нагревании металла на платиновых электродах, затем они ускоряются электрическим полем и отбрасываются. Нагрев может производиться солнечной энергией. Ракета такого типа может работать только в вакууме. Ее параметры следующие. Скорость истечения ионов 150 км/с, напряжение на электродах 10 кВ, ионный ток 660 А, тяга двигателя 90 Н, ускорение 3,5.10^-5 g , расход топлива 0,59 г/с. Зеркала площадью 76 000 м² позволяют получить тепловую мощность 7 600 кВт. Конечно, атомный реактор также может быть использован для ионизации атомов, но при этом из-за необходимости иметь биологическую защиту кпд ракеты падает.

Марк Рейман из НАСА реализовал ионный двигатель, который разгоняет космический аппарат от нуля до 100 км/ч (ускорение порядка 8.10^-7g). Этот двигатель уже работает 2 года (август, 2003). С таким двигателем Солнечную систему можно пересечь за несколько месяцев (среднее расстояние от Солнца до Плутона 39,4 х 1,49 .10¹¹ м)

Специалисты считают, что имеется реальная возможность использовать давление света для перемещения в пределах солнечной системы. На орбите Земли эта величина крайне мала, порядка 9.10^-9 Па (при нормальном падении света на идеальный зеркальный отражатель). Поэтому траектории солнечных парусников будут пролегать вблизи Солнца, чтобы набрать как можно большее ускорение. Полагают, что с солнечными парусами можно достичь скоростей порядка 200 км/с.

Применение многоступенчатых ракет эффективно повышает кпд, но имеются технологические трудности при создании ракет с числом ступеней 5 – 6. Кроме того, многоступенчатая ракета не становится автоматически более эффективной. Например, советская трехступенчатая ракета-носитель «Протон» (1965 г) выводила на орбиту массу полезного груза 20 т, а двухступенчатая ракета-носитель «Энергия» (1987 г) – 100 т.

Приведем параметры трехступенчатой ракеты «Сатурн - V» (полезный груз – 100 т, характеристическая скорость – 9,88 км/с достаточна для круговой орбиты высотой 480 км)

Сту пень	Масса топлива, т	Масса конструкции, т	Тяга, кН	Время горения, с	Топливо
1-я	100	10	900	480	Н2/О2
2-я	420	35	4500	390	Н2/О2
3-я	2160	140	34 000	150	керосин/О2
	Скорость истечения, км/с	Расход топлива, т/с	Масса ступени, т	Характеристическая скорость, км/с
1-я	4,25	0,208	210	2,75
2-я	4,1	1,076	665	4,1
3-я	2,32	14,4	2965	3,03

Удельный импульс – отношение скорости истечения к ускорению свободного падения

Окислитель	Горючее	Температура в камере сгорания, К	Пустотный удельный импульс, с
Жидкий кислород	Жидкий водород	3250	428
	Керосин (~ С10Н20)	3755	335
	Диметилгидразин несимметричный	3670	344
	Гидразин (N2Н4)	3446	346
	Жидкий аммиак (NН3)	3070	323
Четырехокись азота	Керосин	3516	309
	Диметилгидразин несим метричный ((СН3)2 N2Н2) (гептил)	3469	318
	Гидразин	3287	322
Жидкий фтор	Жидкий водород	4707	449
	Гидразин	4775	402

Первым белорусским ракетчиком считается Казимир Семенович, выходец, возможно, из Быхова, который в 1650 г. в Амстердаме опубликовал авторитетную книгу «Великое искусство артиллерии», в которой он, по словам профессора А.А. Космодемьянского, «впервые в мире дал чертеж многоступенчатой ракеты».

Борис Кит, родившийся в Новогрудке, был школьным учителем в Вильно, но после войны попал в Германию, а затем в США, где стал ведущим разработчиком и конструктором «North American Aviation», фирмы создавшей первые космические системы. Затем он становится экспертом и советником правительства США в области развития астронавтики.

Эти мена вписаны в историю ракетной техники наряду с именами англичанина У. Конгрева, француза Р.Эно-Пельтри, американца Х. Годарда, немцев Г. Оберта и В. фон Брауна, русских К.Э. Циолковского и С.П. Королева. Еще один наш земляк – Павел Осипович Сухой (1895 - 1975) из Глубокого, что на Витебщине, по праву считается создателем лучших в мире реактивных самолетов – тех же ракет, но с крыльями, на которых установлены мировые рекорды высоты (1959 и 1962 г.г.) и скорости (1960 и 1962 г.г.).