
- •Методические указания по выполнению контрольной работы №2.
- •Пояснительная записка
- •Общие методические указания по выполнению домашних контрольных работ
- •Методические указания по изучению разделов и тем дисциплины « Техническая механика»
- •Раздел 1. Теоретическая механика
- •Введение
- •Тема 1. 2.1 Основные понятия кинематики.
- •Тема 1. 2.2 Простейшие движения твердого тела.
- •Тема 1. 2.3 Сложное движение твердого тела.
- •Тема 2.5. Изгиб.
- •Тема 2.6. Изгиб с кручением.
- •Тема 2.7. Устойчивость сжатых стержней.
- •Раздел 3. Детали машин
- •Задания для контрольной работы №1
- •Методические указания по выполнению контрольной работы
- •5.1 Задания 1и 2 по теме «Система сходящихся сил»
- •5.1.1. Рекомендуемая последовательность решения задания 1 и 2.
- •5.1. 2. Пример 1. Определение усилий в стержнях
- •5.2 Задания 3 и 4по теме «Плоская систем произвольных сил»
- •5.2.1. Рекомендуемая последовательность решения задания 3и 4.
- •5.2.2. Пример 2. Определение опорных реакций заделки
- •5.3. Задание 5 по теме «Центр параллельных сил и центр тяжести»
- •5.3.1. Рекомендуемая последовательность решения задания 5
- •5.4 Задание 6 по теме «Движение материальной точки. Метод кинетостатики»
- •5.4.1. Рекомендуемая последовательность решения задания 6
- •5.7 Задание 9 по теме «Кручение»
- •5.7.1. Последовательность решения задачи 5
- •5.8. Задание 10 по теме «Изгиб»
- •5.8.1 Рекомендуемая последовательность решения задания 6
- •5.8.2. Пример 5.
- •1 Участок:
- •2 Участок :
- •Экзаменационные вопросы Введение
- •Раздел 1. Теоретическая механика
- •Тема 1.1 Основные понятия и аксиомы статики
- •Тема 1.2. Плоская система сходящихся сил
- •Тема 1.3. Пара сил и момент силы относительно точки
- •Тема 1.4. Плоская система произвольно расположенных сил
- •Тема 1.5. Центр тяжести
- •Темы 1.6 - 1.9. Кинематика. Динамика
- •Раздел 2. Сопротивление материалов
- •Тема 2.1. Основные положение. Растяжение и сжатие
- •Тема 2.2. Практические расчеты на срез и смятие
- •Тема 2.3. Геометрические характеристики плоских сечений
- •Тема 2.4. Кручение
- •Тема 2.5. Изгиб
- •Тема 2.6. Гипотезы прочности и их применение
- •Методические рекомендации по изучению раздела 3 « Детали машин».
- •Задания для контрольной работы №2
- •7.2 Рекомендуемая последовательность решения задания 1
- •Экзаменационные вопросы Раздел 3. Детали машин
- •Тема 3.1. Основные положения
- •Тема 3.2. Соединения деталей
- •Тема 3.3. Общие сведения о передачах. Расчет основных
- •Тема 3.4. Фрикционные и ременные передачи
- •Тема 3.5. Зубчатые и цепные передачи. Редукторы
- •Тема 3.6. Валы и оси. Шпоночные и шлицевые соединения.
- •Тема 3.7. Подшипники
5.2 Задания 3 и 4по теме «Плоская систем произвольных сил»
5.2.1. Рекомендуемая последовательность решения задания 3и 4.
1. Балку освободить от связей (связи) и их (его) действие заменить силами реакций.
2. Выбрать координатные оси.
3. Составить и решить уравнения равновесия.
Реакции опор можно определить, исходя из трех форм уравнений равновесия:
а) Fкх = 0; б) Fкх = 0; в) МА = 0;
Fку = 0 МА = 0; МВ = 0;
МА = 0; МВ = 0; МС = 0.
4. Проверить правильность решения задачи. Проверку необходимо производить по тому уравнению равновесия, которое не было использовано при решении данной задачи. (задача решена правильно лишь в том случае, если после постановки значений активных и реактивных сил в уравнение равновесия выполняется условие равновесия).
5. Сделать анализ решенной задачи (если при решении задачи реакции опор или реактивный момент получается отрицательным, то их действительное направление противоположно принятому).
5.2.2. Пример 2. Определение опорных реакций заделки
Горизонтальная
балка, поддерживающая балкон, подвергается
действию равномерно распределенной
нагрузки интенсивностью q
= 2 кН/м в соответствии с рисунком 14. На
балку в точке С передается нагрузка от
колонны P
= 2 кН;
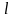 = 1,5 м. Определить реакции заделки А.
= 1,5 м. Определить реакции заделки А.
Решение
1. Освобождаем балку от опоры, заменив ее опорными реакциями.
2. Выбираем расположение координатных осей (рисунок 12).
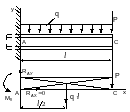
Рисунок 12
3. Применим условие равновесия плоской системы параллельных сил и составим два уравнения равновесия
Fку
= RАу–
q
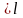 - Р = 0;
- Р = 0;
RАу = q + Р ;
RАу
= 2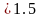 + 2 = 5 кН;
+ 2 = 5 кН;
МА
= - МR+
q
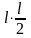 + P
= 0;
+ P
= 0;
МR = q + P ;
МR
= 2
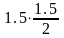 + 2
= 5,25 кНм.
+ 2
= 5,25 кНм.
Горизонтальная составляющая RАх = 0, так как горизонтальные активные силы отсутствуют.
4. Проверяем правильность найденных результатов.
М
С = -
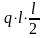 - MR
+
- MR
+
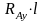 = 0: -
= 0: -
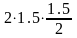 - 5,25 +
- 5,25 +
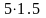 = 0
= 0
5. Условие равновесия М С = 0 выполняется, следовательно, реакции опоры найдены верно.
5.3. Задание 5 по теме «Центр параллельных сил и центр тяжести»
5.3.1. Рекомендуемая последовательность решения задания 5
В задаче требуется определить координаты центра тяжести однородной пластинки, разбив ее на простые геометрические фигуры. Задачу решить рациональным способом, т.е. простых фигур должно быть минимальное количество. Последовательность решения задач следующая:
проводим оси координат таким образом, чтобы они охватывали всю пластинку;
разбиваем пластинку сложной формы на простые геометрические фигуры;
определяем координаты центров тяжести простых фигур и их площади;
определяем координаты центра тяжести пластинки по формулам:
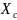 =
=
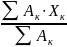 ,
,
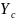 =
=
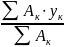 .
.
5.4 Задание 6 по теме «Движение материальной точки. Метод кинетостатики»
