Министерство образования и науки Украины

Одесский национальный морской Университет

Кафедра теории корабля им. проф. Ю.Л. Воробьева

Теория корабля (качка)

Методические указания по проведению лабораторных работ

Исследование бортовой качки модели судна

Одесса – 2016

Методические указания подготовлены кандидатом технических наук Демидюком Александром Владимировичем – доцентом «Кафедры теории и проектирование корабля им. проф. Ю.Л. Воробьева» Одесского национального морского унивекситета и Дригой Мариной Витальевной - старшим преподавателем этой же кафедры

Методические указания одобрены кафедрой ТиПК ОНМУ 23 апреля 2016 года (протокол № )

Содержание

Цель работы	4
Лабораторная работа № 1. Определение веса модели и перемещение ее центра тяжести на одну вертикаль с центром величины	4
Лабораторная работа № 2. Определение периода колебаний модели в воздухе.	5
Лабораторная работа № 3. Определение собственного момента инерции модели.	6
Лабораторная работа № 4. Определение присоединенного момента инерции масс модели	9
Лабораторная работа № 5. Определение коэффициента сопротивления при бортовой качке и пересчет характеристик качки на натурное судно	10
Оформление работы	11
Список использованной литературы	11
Пример оформления протокола работ	12
Кривые элементов теоретического чертежа	19

Цель работы

В процессе выполнения лабораторной работы определяются водоизмещение судна , положение его центра тяжести и , присоединенный момент инерции масс воды , период свободных колебаний , коэффициент сопротивления при бортовой качке .

Для проведения работы изготовлена модель транспортного судна со следующими главными размерениями:

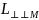=1,53 м

=0,274 м

=0,077 м

=0,81

=26,3 кг

=0,015м

Модель изготовлена в масштабе

Лабораторные работы представляют собой ряд самостоятельных задач и проводятся на лабораторных занятиях во время изучения курса «Теория корабля (Качка)».

Лабораторная работа № 1. Определение веса модели и перемещение ее центра тяжести на одну вертикаль с центром величины

1.1 Модель устанавливается на весы и догружается гирями до веса =26,3 кг. Гири произвольным образом размещаются на носовой и кормовой вертикальных стойках (рис. 1). Расстояние от каждой стойки до миделя 0,65 м.

1.2 Для определения положения центра тяжести по длине модель помещается на опоры А и В (рис. 1), где АВ= =1,68 м. Если показание весов , то расстояние от центра тяжести модели до миделя с учетом направления продольной оси х определяется по формуле

(1)

где

(2)

d – расстояние между центром тяжести модели и опорой В, м;

=-0,605 м – абсцисса точки В.

1.3 Для того, чтобы модель плавала на воде в положении «на ровный киль» необходимо выполнить условие миделя

(3)

После определения текущего значения 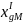может оказаться, что . Тогда вычисляется разность

(4)

и определяется вес груза , который необходимо перенести с одной вертикальной стойки на другую (из условия равенства моментов весов):

(5)

Если 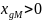, то груз переносится с кормовой стойки на носовую, если – наоборот.

1.4 После переноса груза абсцисса центра тяжести модели определяется во втором приближении способом, описанным в пункте 1.2, с последующей проверкой условия (3). Если условие (3) выполняется ( ), то процесс вычисления абсциссы центра тяжести заканчивается. В противном случае снова определяется вес груза , подлежащего переносу и т.д.

Условие (3) должно выполняться с точностью до =0,001 м. Результаты измерений и вычислений записываются в таблицу 1.

Лабораторная работа № 2. Определение периода колебаний модели в воздухе.

Период колебаний модели в воздухе необходим нам, чтобы в дальнейшем определить момент инерции масс модели относительно продольной оси, проходящей через ее центр тяжести ( ).

Для определения упомянутых величин модель подвешивают в воздухе на специальной установке (рис. 2). Для этого на модели имеется соответствующее приспособление.

Подвешенная модель может колебаться вокруг оси О, т.е. представляет собой физический маятник, период колебаний которого связан с моментом инерции масс модели относительно оси колебаний О. Колебания модели, как физического маятника, будут затухающими поскольку энергия будет расходоваться на преодоление сопротивления воздуха и на трение в месте подвеса.

Поэтому амплитуда колебаний будет постоянно уменьшаться, а период – оставаться постоянным.

Период свободных колебаний определяется следующим образом. С помощью секундомера измеряется продолжительность ( ) большого числа колебаний ( ) и период колебаний ( ) вычисляется по формуле.

(6)

Опыт по определению повторяется несколько раз. Причем отсчет времени следует начинать после того, как модель совершит несколько полных колебаний и движение будет установившимся.

Результаты измерений и вычислений заносятся в таблицу 2. Учитывать следует только те результаты, которые незначительно отличаются между собой. Значения периода, которые резко отличаются от остальных, следует исключить из рассмотрения, поскольку они свидетельствуют о неточности проведения данного опыта.

Лабораторная работа № 3. Определение собственного момента инерции модели.

3.1 Собственный момент инерции масс модели. - это момент инерции относительно оси проходящей через центр тяжести масс модели.

Момент инерции относительно любой оси, параллельной оси, относительно которой определен собственный момент инерции, будет больше по величине, чем на величину так называемого переносного момента инерции, который равен произведению массы тела на квадрат расстояния между вышеупомянутыми осями.

Момент инерции модели относительно любой оси, не проходящей через центр тяжести модели, связан с периодом колебаний. Рассмотрим момент инерции относительно упомянутой выше оси О – горизонтальной оси подвеса модели.

(7)

где

– момент инерции масс модели относительно оси О колебаний , кгмс²;

– расстояние от оси до центра тяжести модели, м.

(8)

Cобственный момент инерции масс модели

(9)

В формуле (8) Н – расстояние от основной плоскости до оси подвеса, его следует измерить линейкой.

Аппликата центра тяжести модели будет определена в опыте кренования.

3.2 Опыт кренования. Модель устанавливается на воду и проверяется правильность ее посадки по конструктивную ватерлинию, нанесенную на борт модели. Крен модели судна на малый угол создается кренящим моментом ( ), как показано на рис. 3.

Если – вес каждого из грузов, установленного на штырь (4) и подвешенного к тросику (3), а – расстояние между штырями, то

.

(9)

где – угол крена в градусах.

Угол в (9) определяется при помощи кренометра, установленного на модели.

Кренометр представляет собой металлический сосуд, заполненный вязкой жидкостью. В жидкость опущена гибкая пластиковая полоска, к которой прикреплен тензодатчик.

При накренении модели полоска меняет свою форму, тензодатчик растягивается либо сжимается, вследствие чего меняется его сопротивление.

С тензодатчика сигнал через аналогово-цифровой преобразователь подается на компьютер, где при помощи специального программного обеспечения записывается в виде графика. На этом графике по горизонтальной оси изображается время, а по вертикальной – так называемые условные коды, связанные с напряжением на тензодатчике.

3.3 Тарировка кренометра

Для того, чтобы с помощью кренометра можно было получать значения угла крена модели в градусах, необходимо предварительно произвести тарировку прибора. То есть сопоставить показания прибора в условных кодах с его положением в пространстве.

Для этого используется специальный лимб в форме кольца, на котором закреплен стакан, в который можно поместить кренометр. На лимбе находится шкала, проградуированная в градусах. Стакан может вращаться вокруг оси, перпендикулярной плоскости лимба.

Следует поместить кренометр в стакан. Затем стакан отклонять от вертикали последовательно на 2, 4, 6, 8, 10 градусов, причем сначала вправо, а потом влево. При этом записывается сигнал в условных кодах, поступающий с кренометра. Таким образом, мы можем построить зависимость между показаниями кренометра в условных кодах и углом между осью симметрии кренометра и вертикалью. Этот график называется тарировочной кривой. Мы берем абсолютные значения углов в градусах и условных кодах, и строим зависимости для наклонения влево и вправо в одной системе координат, а затем в качестве тарировочной кривой принять линию, равноудаленную от указанных кривых. Примерный вид тарировочной кривой показан на рис. 4.

Опыт кренования повторяется несколько раз для разных значений веса грузов , и, соответственно каждый раз вычисляется значение метацентрической высоты.

После вычисления среднего значения метацентрической высоты (см. табл. 4), следует определить аппликату центра тяжести модели

(10)

– аппликата центра величины модели,

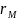– поперечный метацентрический радиус модели.

Эти величины находятся с помощью кривых элементов теоретического чертежа (см. рис.5)

Лабораторная работа № 4. Определение присоединенного момента инерции масс модели