МЕТОДИЧЕСКАЯ РАЗРАБОТКА

Материалы для самоподготовки

к ЕГЭ и ГИА

по планиметрии

Часть 2

(окружности)

Автор-составитель :

СМИРНОВА

ГАЛИНА ВАСИЛЬЕВНА

АННОТАЦИЯ

Учебно-методические материалы, представленные в данном пособии, предназначаются для самоподготовки школьников и абитуриентов к ЕГЭ и ГИА по математике.

По каждой теме в пособии содержится практически весь необходимый для решения задач теоретический материал, формулы и методические рекомендации. Представлено подробное решение основных видов задач по теме , а также приведено большое количество заданий для самостоятельного решения.

Надеемся, что данное пособие поможет учащимся быстро систематизировать знания и овладеть методами решения задач по планиметрии

СОДЕРЖАНИЕ:

Занятие 8

Окружность и круг . Основные понятия и свойства.

Длина окружности и площадь круга

Углы, связанные с окружностью.

Касательная к окружности, хорды, секущие. Их свойства.

Занятие 9

Теорема синусов. Теорема косинусов.

Теорема о биссектрисе внутреннего угла треугольника

Занятие 10

Вписанные и описанные около треугольника окружности. Вневписанная окружность.

Занятие 11

Вписанные и описанные около четырехугольника окружности.

Занятие 12

Правильные многоугольники и соотношения в них.

Занятие 8

Окружность и круг . Основные понятия и свойства.

Длина окружности и площадь круга

Углы, связанные с окружностью.

Касательная к окружности, хорды, секущие. Их свойства.

Окружность и круг. Основные понятия и свойства. Длина окружности и площадь круга

Окружность — замкнутая кривая, все точки которой одинаково удалены от данной точки (центра).

Круг — часть плоскости, ограниченная окружностью.

Радиус— отрезок прямой, соединяющий центр окружности с какой-либо её точкой/

Отрезок, соединяющий две точки окружности, называется хордой.

Хорда, проходящая через центр окружности называется диаметром. Диаметр окружности равен двум радиусам.

Отношение длины окружности к её диаметру одинаково для всех окружностей. Это отношение есть трансцендентное число, обозначаемое греческой буквой пи: π=3,14159...

Длина окружности: С = 2πR

Площадь круга

Сектором круга называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Сегментом называется  часть круга, ограниченная дугой и стягивающей её хордой.

Площадь сектора равна , где α — угловая величина дуги в радианах, R — радиус. Длина дуги такого сектора вычисляется по формуле . Если угол , то

Свойства хорд и касательных

ТЕОРЕМА Диаметр, перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам.

ТЕОРЕМА Диаметр, проведенный через середину хорды (дуги) , перпендикулярен этой хорде.

ТЕОРЕМА Дуги, заключенные между параллельными хордами, равны.

ТЕОРЕМА В одном круге ( или в равных кругах) если дуги равны, то равны и стягиваемые ими хорды и наоборот.

ТЕОРЕМА В одном круге ( или в разных кругах) равные хорды равноудалены от центра, и наоборот, если хорды равноудалены от центра , то они равны.

Прямая, имеющая с окружностью ровно одну общую точку называется касательной к окружности.

ТЕОРЕМА Если прямая касательная к окружности, то она перпендикулярна к радиусу, проведенному и точку касания.

ТЕОРЕМА Если прямая перпендикулярна радиусу, проведенному через общую точку прямой и окружности, то прямая касательная к окружности.

ТЕОРЕМА Две касательные, проведенные к окружности из одной точки, равны и образуют равные углы с прямой, соединяющей эту точку с центром окружности.

ТЕОРЕМА Если две окружности имеют общую точку, расположенную вне линии центров, то они имеют и другую общую точку, симметричную с данной относительно линии центров.

ТЕОРЕМА Общая хорда двух пересекающихся окружностей перпендикулярна к линии центров и делится ею пополам.

ТЕОРЕМА Если две окружности касаются, то точка касания лежит на линии их центров.

ТЕОРЕМА Если через точку, взятую внутри круга, проведены хорда и диаметр, то произведение отрезков хорды равно произведению отрезков диаметра.

Следствие: если через точку внутри круга проведены хорды, то произведение отрезков этих хорд есть величина постоянная.

ТЕОРЕМА Если из точки вне круга проведены к нему касательная и секущая, то квадрат касательной равен произведению секущей на ее внешнюю часть.

Следствие: если из точки вне круга проведены к нему секущие, то произведение секущей на ее внешнюю часть есть величина постоянная.

Углы, связанные с окружностью

Угол, образованный двумя хордами, проведенными из одной точки, называется вписанным.

ТЕОРЕМА Вписанный угол измеряется половиной дуги, на которую он опирается.

Следствия:

все вписанные углы, опирающиеся на одну и ту же дугу, равны ;

вписанный угол, опирающийся на диаметр, прямой.

ТЕОРЕМА Угол, вершина которого лежит внутри круга, измеряется полусуммой двух дуг, заключенных между его сторонами

ТЕОРЕМА Угол, вершина которого лежит вне круга, а стороны пересекаются с окружностью, измеряется полуразностью двух дуг, заключенных между его сторонами.

ТЕОРЕМА Угол, составленный касательной и хордой, измеряется половиной дуги, заключенной внутри угла.

Задания с решением

1. Найдите величину угла АВС. Ответ дайте в градусах.

Решение.

Построим квадрат со стороной АС.

Тогда видно, что угол АВС опирается на окружности, то есть на дугу 90º. Вписанный угол равен половине дуги, на которую он опирается, значит

Ответ 45º

2. Хорда АВ делит окружность на две части, градусные величины которых относятся как 6:12. Под каким углом видна эта хорда из точки С, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.

Решение.

Из точки C хорда АВ видна под углом АCВ. Пусть большая часть окружности равна 12х, тогда меньшая равна 6х. Вся окружность составляет 360º.

Получаем уравнение 12х+6х=360º.Откуда х=20º.

Угол АСВ опирается на большую дугу окружности, которая равна 12·20º=240º.

Вписанный угол равен половине дуги, на которую он опирается, значит, опирающийся на большую дугу угол АCВ равен

Ответ 120º

3. Хорда АВ стягивает дугу окружности в 84º. Найдите угол АВС между этой хордой и касательной к окружности, проведенной через точку В. Ответ дайте в градусах.

Решение.

Угол АВС – это угол между касательной и хордой. Он измеряется половиной дуги, заключенной внутри угла. Дуга внутри угла равна 84º.Значит

Ответ 42º

4. К окружности радиуса 36 проведена касательная из точки, удаленной от центра на расстояние, равное 85. Найдите длину касательной.

Решение

Пусть ОА=36, ОС=85.Радиус, проведённый в точку касания, перпендикулярен касательной. Из прямоугольного треугольника АОС по теореме Пифагора получаем

Ответ 77

5. К окружности из точки С вне ее проведены касательная АС и секущая СD, пересекающая окружность в точке В. Сумма длин касательной и секущей равна 30см , а внутренний отрезок секущей на 2см короче касательной. Найти длины касательной и секущей.

Решение

Пусть АС=х, а СD=у. Тогда х+у=30, а DB=AC-2=x-2 , BC=AC-DB=y-DB=y-(x-2)=y-x+2. По теореме, если из точки вне круга проведены к нему касательная и секущая, то квадрат касательной равен произведению секущей на ее внешнюю часть, то есть . Тогда

Получаем систему

. х=80 не подходит так как у>0 Поэтому получаем

Касательная АС=12, секущая CD=18.

Ответ 12 и 18

6. Найти площадь S закрашенного сектора. В ответе укажите S/π.

Решение

Построим на данном чертеже квадрат

Тогда становится очевидно, что сектор составляет одну четверть круга.

Радиус равен половине диагонали квадрата, сторона которого равна 4.

Тогда площадь сектора вычислим по формуле

Тогда искомая величина равна

Ответ 2

Чему равен вписанный угол, опирающийся на диаметр окружности? Ответ дайте в градусах.	Найдите хорду, на которую опирается угол 90º, вписанный в окружность радиуса 1.
Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.	Найдите хорду, на которую опирается угол 30º, вписанный в окружность радиуса 3.
Чему равен тупой вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.	Радиус окружности равен 1. Найдите величину острого вписанного угла, опирающегося на хорду, равную . Ответ дайте в градусах.
Радиус окружности равен 1. Найдите величину тупого вписанного угла, опирающегося на хорду, равную . Ответ дайте в градусах.	Найдите хорду, на которую опирается угол 120º, вписанный в окружность радиуса .
Центральный угол на 34º больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.	Найдите величину угла ABC. Ответ дайте в градусах.
Найдите величину угла ABC. Ответ дайте в градусах.	Найдите градусную величину дуги AC окружности, на которую опирается угол ABC. Ответ дайте в градусах.
Найдите градусную величину дуги BC окружности, на которую опирается угол BAC. Ответ дайте в градусах.	Угол ACO равен 25º, где O  — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.
Найдите угол ACO, если его сторона CA касается окружности, O— центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 110º. Ответ дайте в градусах.	Найдите угол ACB, если вписанные углы ADB и DAE опираются на дуги окружности, градусные величины которых равны соответственно 116º и 36º . Ответ дайте в градусах.
Угол ACB равен 50º. Градусная величина дуги AB окружности, не содержащей точек D и E, равна 130º. Найдите угол DAE. Ответ дайте в градусах.	Хорда AB стягивает дугу окружности в 86º. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.
Угол между хордой AB и касательной BC к окружности равен 28º. Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.	Через концы A, B дуги окружности в 72º проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.
Касательные CA и CB к окружности образуют угол ACB, равный 112º. Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.	Найдите угол ACO, если его сторона CA касается окружности, O  — центр окружности, а дуга меньшая дуга окружности AB, заключенная внутри этого угла, равна 62º. Ответ дайте в градусах.

1. Найдите площадь круга, длина окружности которого равна .

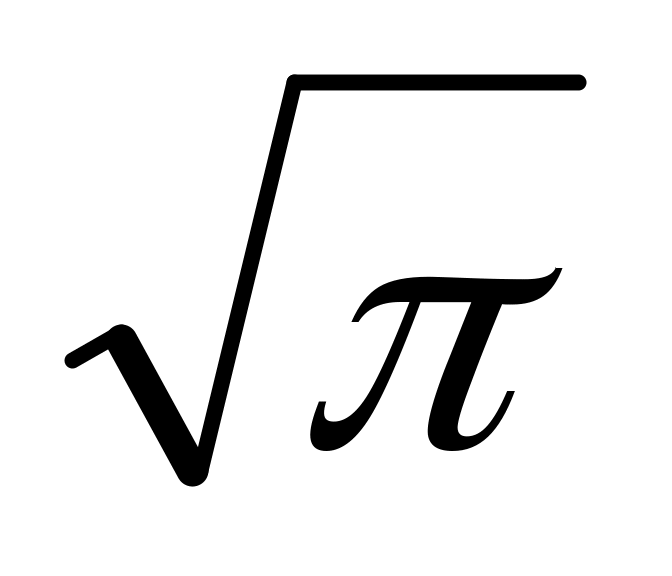2. Площадь круга равна . Найдите длину его окружности.

3. Найдите площадь сектора круга радиуса , центральный угол которого равен 90º .Найдите площадь сектора круга радиуса 1, длина дуги которого равна 2.

4. Хорда делит окружность в отношении 5 : 13. Найти величины вписанных углов, опирающихся на эту хорду.

5. Хорда делит окружность в отношении 11 : 7. Найти угол между касательными, проведенными из концов хорды.

6. Окружность разделена в отношении 5 : 9 : 10, и через точки деления проведены касательные, найти больший угол в полученном треугольнике.

7. На боковой стороне равнобедренного треугольника как на диаметре построена полуокружность. Стороны треугольника делят полуокружность на три дуги. Найти угловые величины этих дуг, если угол при вершине треугольника равен 40º.

8. Окружность разделена точками A, B, C, D на дуги, угловые величины которых относятся как . Найти величины углов между прямыми АВ и CD, АС и BD...

9. Центральный угол на 35º больше вписанного угла, опирающегося на ту же дугу. Найдите каждый из этих углов.

10. Найдите вписанный угол, опирающийся на дугу, которая составляет 10 % окружности.

11. Сколько спиц в колесе, если угол между соседними спицами равен 18º?

12. Какой угол (в градусах) образуют минутная и часовая стрелки часов в 5 ч?

13. Какой угол (в градусах) описывает минутная стрелка за 10 мин?

14. Какой угол (в градусах) описывает часовая стрелка за 20 мин?

15. На какой угол (в градусах) поворачивается минутная стрелка пока часовая проходит 2º?

16. Из точки вне круга проведены две секущие.Внутренний отрезок первой равен 47, а внешний 9.Внутренний отрезок второй секущей на 72 больше ее внешнего отрезка. Найти длину второй секущей.

17. Радиус круга равен 5. Найти длину дуги сектора с углом в 36º.

18. Длина общей хорды двух кругов радиуса равна 2.Найти площадь общей части этих кругов.

19. Найти площадь сегмента , если радиус равен 6, а дуга 90º.

20. Прямая делит окружность на две дуги, длины которых относятся как 1:3.В каком отношении эта прямая делит площадь круга.

21. Расстояние от центра окружности до хорды равно и вдвое меньше радиуса. Найти длину хорды.

22. Радиус окружности равен 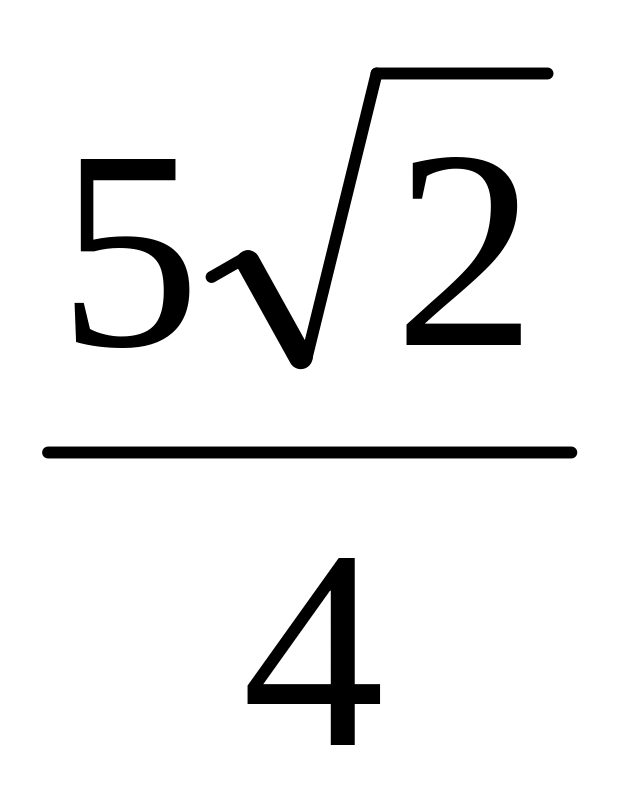.Найти расстояние от центра окружности до хорды, если она стягивает угол 90º.

23. Длина хорды равна . Найти расстояние от центра окружности до хорды, если она стягивает дугу 120º.

24. Из точки вне окружности проведены к ней две касательные. Длина каждой касательной равна 13, а расстояние между точками касания равно 24.Найти длину радиуса окружности.