2.3 Вклад г. Ламэ
Следующую после Дж. Шведлера попытку расчета ферм мы встречаем в 1852 г. в книге Г. Ламэ. Вопреки легенде, пущенной кем-то из авторов исторических обзоров, Г. Ламэ не рассматривал статически неопределимые фермы, а ограничился статически определимыми, причем применил к их расчету принцип возможных перемещений. Г. Ламе составил на основе известного «принципа Клапейрона» формулу для вычисления перемещений фермы под грузом и искал формы сооружений, дающих минимальный прогиб при условии равнопрочности [1].
2.4 Работы Августиновича
Мысль о применении принципа возможных перемещений к расчету ферм использовал русский инженер Августинович [5], распространивший ее на статически неопределимые фермы (1857 г.). Это была первая после Д. И. Журавского попытка расчета таких ферм, на этот раз теоретически правильная, в основе которой лежала идея Д. И. Журавского. Таким образом первый правильный метод расчета статических неопределимых ферм принадлежит Августиновичу. Это определяет первенство русских ученых в данной области.
В работах Августиновича, в отличие от Д. И. Журавского четко прослеживаются разграничения между статически определимыми фермами и статически неопределимыми.
Для расчета статически определимой фермы с n узлами Августинович составляет 2n уравнений проекции возможных перемещений, задавая их следующим правилом: «если линия наклонна, то пишется ее коэффициент, помноженный на проекцию; а если линия горизонтальна или вертикальна, то пишется коэффициент, наблюдая в отношении знаков, следующее правило: для отдаленных от осей концов линии член пишется с плюсом; для ближайших к осям - с минусом». Под «коэффициентом» понимается усилие в стержне или величина, ему пропорциональная. В приведенных Августиновичем примерах эти «коэффициенты» равны усилиям в стержнях, деленым на их длины.
Рис. 5 - Обозначения Августиновича
По этому правилу уравнения перемещений для узла l (рис. 5) примут вид:
-
(2)
Если подставить вместо M, N, L усилия в стрежнях, деленные на длины, мы получим обычные уравнения равновесия.
Разумеется, составление и решение системы из 2n уравнений для фермы с n узлами очень трудоемко (как и метод вырезания узлов в общем случае). Августинович это осознает и заявляет, что на данном этапе развития науки отсутствует метод, который мог бы прийти на помощь в данной ситуации.
Рис. 6 - Первая статически неопределимая ферма, рассчитанная Агустиновичем.
Конечно,
способ введенный Августиновичем не
облегчал внедрения расчета ферм в
проектную практику; с точки зрения
трудоемкости он даже представлял
некоторый шаг назад. При этом чрезвычайно
оригинальным можно считать способ,
предложенный Августиновичем для расчета
статически неопределимых ферм, поясненный
им на примере фермы (рис. 6). Эта распорная
ферма имеет при симметричном загружении
два лишних неизвестных
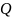и
.
Для их определения необходимо составить
два условия деформации, выражающие
постоянство длин проекции на горизонтальную
ось обоих поясов. При постоянной длине
панели и равенстве сечений элементов
пояса (допущения Августиновича) можно
составить условия равенства нулю суммы
проекций удлинений поясов в виде:
-
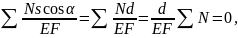
(3)
Откуда
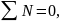т. е. алгебраическая сумма усилий в
элементах каждого пояса должна быть
равна нулю.
Здесь
s
– длина элемента пояса;
– длина
панели; N
–
усилие в элементе пояса.
Вместо
этого Августинович вспоминает «задачу
Жуковского» о действии осевых сил на
стержень и обобщает ее, полагая, что к
стержню приложены на равных расстояниях
продольные силы
.
Применяя закон приложения нагрузок, Августинович вычисляет реакции по концам стрежня:
-
(4)
Затем
он доказывает, что решение остается
справедливым, если стержень имеет
ломаную форму: проекции удлинения
системы abcde
таковы, как если бы прямой стержень af
был натянут силой P.
Отсюда Августинович заключает, что
вышенаписанные уравнения останутся
справедливыми, если вместо сил P
подставить горизонтальные составляющие
узловых поясных сил, как это делал Д. И.
Журавский. При этом реакции, вычисленные
по этим уравнениям, будут равны искомым
реакциям фермы
в зависимости от того, для какого узла
пояса взяты узлы.
Рис. 7 - Лемма Августиновича
Этот способ является довольно оригинальным. Но большого практического распространения, так как расчет является крайне трудоемким. Так или иначе, это первый правильный расчет статически неопределимой фермы.