Первые методы расчетов

2.1 Работы д. И. Журавского

Краткая оценка работ Дмитрия Ивановича Журавского в области расчета ферм приведена в «Курсе строительной механики стержневых систем» проф. И. М. Рабиновича (ч. 1, 1950, стр. 279-280) [3]. Он разработал метод расчета фермы Гау на нагрузку, занимающую произвольное положение в, а также сделал попытку расчета многопролетной неразрезной фермы такой схемы. Результаты опубликованы в журнале Главного управления путей сообщения в виде трех статей в 1850, 1852, 1855 гг., а затем изданы отдельной книгой в 1855 г. На основе данных результатов расчета Д. И. Журавский впервые обнаружил ряд особенностей в работе ферм, до этого неизвестных, в частности явление убывания усилий в стойках раскосной фермы от опор к середине пролета при сплошной нагрузке. Для доказательства открытия был поставлен публичный опыт.

Д. И. Журавский указывал, что, владея расчетом он доказывал неправильность конструкции стефенсоновских трубчатых мостов, ошибочность мнения Лонга о влиянии предварительного натяжения болтов и ошибочность американских воззрений на сопротивление поясов.

Указание на ошибку Лонга интересно тем, что в той задаче Д. И. Журавский сделал существенное открытие. Речь идет о работе болтовой стяжки, имеющей начальное натяжение. В то время было принято считать, основываясь на мнении Лонга, что усилие в болте от продольной растягивающей нагрузки складывается с усилием от начального натяжения. Д. И. Журавский доказал, наоборот, что «напряжение болтов при нагрузке не состоит из суммы предварительного напряжения от завинчивания болтов и напряжения, производимого собственной нагрузкой, как это могло бы показаться с первого взгляда». Это высказывание Д. И. Журавского является верным: если к головке болта приложить растягивающую силу, то усилие в болте начнет возрастать лишь после того, как стянутые начальным натяжением болта элементы восстановят свои первоначальные размеры. Очевидно, это произойдет, когда внешняя сила станет равна начальному натяжению.

Для расчета фермы Гау Д. И. Журавский берет расчетную схему в виде простой раскосной решетки с восходящими раскосами и шарнирными узлами [3]. Таким образом, распространенное мнение, приписывающее Дж. Шведлеру заслугу введения шарнирной схемы фермы, является ошибочным: эта заслуга всецело принадлежит Д. И. Журавскому, как и идея пренебречь встречными растянутыми раскосами.

Рис. 2 - Расчет фермы Гау методом Жуковского

Д. И. Журавский обосновал это пренебрежение тем, что узловые соединения деревянных раскосов не способны воспринимать растягивающие усилия.

Д. И. Журавский не начинает с определения опорных реакций фермы, как мы это делаем теперь, а прослеживает судьбу каждого груза от точки его приложения до опор. Возьмем простейший случай: груз Р стоит в среднем узле верхнего пояса. Вырежем узел и найдем из условий равновесия и симметрии сжимающие усилия в раскосах . Эти усилия передаются на нижние узлы, из равновесия которых находим растягивающие усилия в стойках 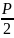и горизонтальную силу , действующую вдоль нижнего пояса. В действительности, эта сила равна разности усилий в двух смежных панелях нижнего пояса, но Д. И. Журавский этим пренебрегает и продолжает процесс вырезания узлов по зигзагу решетки. В результате, он находит усилия во всех раскосах и стойках, и горизонтальные силы, приложенные в узлах и имеющие обратные направления, в отличие от ранее найденных сил [3].

Силы выражали действие стержней на узел, а горизонтальные силы - действие узлов на пояса. Очевидно, усилие в любой панели пояса численно равно сумме горизонтальных сил, приложенных к узлам по одну сторону от панели, и решение получается совершенно точным, несмотря на то, что реакции предварительно не были определены [3].

Этот метод расчета интересен с двух точек зрения. Во-первых, он основан на идее вырезания узлов и составлений условий равновесия, и, таким образом, открытие и первое применение метода вырезания узлов безусловно принадлежит Д. И. Жуковскому.

Во-вторых, (в этом он отличается от современной формы метода вырезания узлов, идущей от К. Кульмана и Дж. Шведлера), Д. И. Журавский не ищет при вырезании узлов усилий в элементах пояса, а находит разность (равнодействующую усилий в двух смежных панелях, это освобождает от необходимости решения совместных уравнений, хотя в каждом следующем узле встречаются три неизвестных усилия. Идея Д. И. Журавского незаслуженно подверглась впоследствии забвению и могла найти и теперь удачное применение при расчете сложных ферм.

В том случае, когла сила Р стоит не в среднем узле, Д. И. Журавский разбирает силу на две части yP и (1-y)P, где y – неопределенный множитель, далее ведет разложение каждой составляющей по узлам в свою сторону. Затем он составляет уравнение равновесия горизонтальных узловых сил и находит из него значение y. Легко заметить, что yP и (1-y)P будут равны опорным реакциям.

Расчет раскосной фермы, данный Д. И. Журавским, вполне точен при любом положении нагрузки. В частности, при равномерном загружении всех узлов наибольшее усилие в поясе оказывает равным где P – узловая нагрузка, l – пролет, n – число узлов, h – высота фермы. Разумеется, расчет является условным для фермы с перекрестными раскосами, так как выбор однораскосной схемы должен предшествовать расчету, а до его выполнения нельзя установить какой раскос в каждой панели окажется сжатым. Если в результате какой-либо раскос окажется растянутым, то не представит труда заменить его на встречный. При условии такой поправки расчет фермы с перекрестными раскосами будет довольно точным, поскольку раскосы не способны работать на растяжение.

Далее Д. И. Журавский проводит расчет многопролетной неразрезной фермы. Эта задача статически неопределима

Рис. 3 - Задача Д. И. Журавского

Д. И. Журавский принимает за неизвестную величину перемещение λ точки приложения силы P и находит его из условия равновесия , устанавливая отсюда, что сила P распределяется между участками стержня обратно пропорционально их длинам. Если положение «сечений раздела грузов» в пролетах известно, то предыдущее решение позволяет распределить узловые горизонтальные составляющие между обоими такими сечениями и найти отсюда усилия в поясах. Слабым местом в методе Д. И. Журавского является порядок нахождения этих сечений, для которого он предлагает способ проб, недостаточно обоснованный теоретически. Для неразрезной балочной схемы такими сечениями будут те, в которых касательные к линии прогиба взаимно параллельны. Действительно, условие постоянства длины продольного волокна, отстоящего на y от нейтральной линии, на участке от до выразится:

(1)

Откуда углы наклона касательной в точках и равны между собой. Очевидно, таких пар сечений может быть бесконечное множество, и поэтому одним из них в каждом пролете можно задаться.