
- •Аналитические решения задач динамики и прочности стержневых конструкций
- •Введение
- •История развития методов расчета стержневых систем
- •1.1 Предпосылки
- •Первые методы расчетов
- •2.1 Работы д. И. Журавского
- •2.2 Работы Дж. Шведлера
- •2.3 Вклад г. Ламэ
- •2.4 Работы Августиновича
- •Появление классических методов расчета ферм
- •3.1 Работы у. Дж. Ренкина
- •3.2 Вклад а. Риттера
- •3.3 Работы Дж. К. Максвелла и его «дублеров»
- •Новые методы расчета
- •Работы в области строительной механики за последние годы
- •Основная часть проведенной работы Постановка задачи
- •1 Простая балочная ферма
- •1.1 Расчет простой балочной фермы
- •1.2 Графики прогиба простой балочной фермы
- •Формула прогиба при полностью загруженном поясе
- •Перераспределение жесткостей
- •1.3 Числовой пример простой балочной фермы
- •1.4 Частота колебаний плоской балочной фермы
- •Графики
- •2 Балочная ферма с параллельными поясами и восходящими раскосами
- •2.1 Расчет балочной фермы с параллельными поясами и восходящими раскосами
- •2.2 Графики прогиба балочной фермы с параллельными поясами и восходящими раскосами
- •Формула прогиба при полностью загруженном поясе
- •3 Перераспределение жесткостей балочной фермы с параллельными поясами и восходящими раскосами
- •Числовой пример балочной фермы с параллельными поясами и восходящими раскосами
- •4 Плоская арочная ферма треугольного очертания
- •Графики прогиба арочной фермы
- •5 Пространственная ферма балочного типа
- •5.1 Схема конструкции
- •5.2 Расчет пространственной балочной фермы
- •5.3 Анализ полученного решения
- •Заключение
- •Список использованной литературы
1.2 Графики прогиба простой балочной фермы
На
рисунке 12 представлен график зависимости
прогиба от числа панелей для различных
узлов фермы ( ).
Здесь
).
Здесь
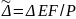 .
.

Рис. 12 - Прогиб фермы в зависимости от числа панелей
На рис. 13 представлен график зависимости прогиба от расстояния между опорами при различных высотах фермы (b = 2 м, b = 3 м, b = 4 м). Здесь .

Рис. 13 - Прогиб фермы в зависимости от пролета
На рис. 14 представлен график зависимости прогиба от высоты фермы при различных расстояниях между опорами (L = 10 м, L = 20 м, L = 30 м). Здесь .

Рис. 14 - Прогиб фермы в зависимости от высоты фермы
Формула прогиба при полностью загруженном поясе

Рис.
15 - Прогиб центрального узла фермы при
равномерно распределенной нагрузке по
нижнему поясу
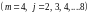
По аналогии с методом, описанным ранее, получена зависимость прогиба центрального узла простой балочной фермы (рис. 15) от числа панелей при нагрузке равномерно распределенной по узлам нижнего пояса:
-

(19)
Перераспределение жесткостей
Уменьшить
прогиб фермы можно, перераспределяя
материал по стержням конструкции.
Предположим, что весь объем материала
равен
 ,
где
,
где
 суммарная
длина всех стержней. Прогиб находим с
помощью формулы Максвелла-Мора [11]:
суммарная
длина всех стержней. Прогиб находим с
помощью формулы Максвелла-Мора [11]:
-
 ,
,
где, –
усилия в i-ом
стержне фермы от приложенной нагрузки
и от единичной вертикальной силы,
приложенной к центральному узлу нижнего
пояса; E
– модуль упругости материала, одинаковый
для всех стержней. Суммирование ведется
по всем стержням фермы, опорные стержни
приняты жесткими и в эту сумму не входят.
Сумма разбита на три части. Первая сумма
относится к группе стержней нижнего и
верхнего поясов, вторая – к вертикальным
стержням решетки, третья – к наклонным
стержням;
–
усилия в i-ом
стержне фермы от приложенной нагрузки
и от единичной вертикальной силы,
приложенной к центральному узлу нижнего
пояса; E
– модуль упругости материала, одинаковый
для всех стержней. Суммирование ведется
по всем стержням фермы, опорные стержни
приняты жесткими и в эту сумму не входят.
Сумма разбита на три части. Первая сумма
относится к группе стержней нижнего и
верхнего поясов, вторая – к вертикальным
стержням решетки, третья – к наклонным
стержням;
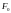 –
усредненная площадь сечения стержня,
–
усредненная площадь сечения стержня,
 коэффициент изменения площади сечения
стержней соответствующих групп. Методом,
описанным ранее, можно также получить
аналитические выражения для прогиба.
Заранее стоит отметить, что
коэффициент изменения площади сечения
стержней соответствующих групп. Методом,
описанным ранее, можно также получить
аналитические выражения для прогиба.
Заранее стоит отметить, что
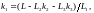 где
где
 суммарная
длина стержней соответствующих групп.
Окончательная формула прогиба принимает
вид:
суммарная
длина стержней соответствующих групп.
Окончательная формула прогиба принимает
вид:
|
(20) |
1.3 Числовой пример простой балочной фермы
Рассмотрим
расчет фермы с
 .
Остальные параметры подобраны с целью
достижения минимального прогиба. В
качестве стержней используются
двутавровые балки из горячекатаной
стали с уклоном внутренних граней полок
(ГОСТ 8239-89) , площадь сечения
.
Остальные параметры подобраны с целью
достижения минимального прогиба. В
качестве стержней используются
двутавровые балки из горячекатаной
стали с уклоном внутренних граней полок
(ГОСТ 8239-89) , площадь сечения ,
масса
,
масса
 .
.
При
нагрузке величиной
 ,
примем
,
примем .
Прогиб центрального узла получается
равным
.
Прогиб центрального узла получается
равным
 ,
а масса конструкции
,
а масса конструкции
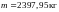 .
.
Уменьшение
прогиба методом перераспределения
жесткостей в этой ферме возможно, при
этом прогиб уменьшается на
 м. В соответствии со СНиП 2.01.07-85 балки,
фермы, ригели, прогоны, плиты и т. д.
должны иметь прогиб порядка
м. В соответствии со СНиП 2.01.07-85 балки,
фермы, ригели, прогоны, плиты и т. д.
должны иметь прогиб порядка
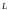 /300
при длине конструкции
=36
м. Таким образом, данная конструкция
отвечает требованиям строительных норм
и правил.
/300
при длине конструкции
=36
м. Таким образом, данная конструкция
отвечает требованиям строительных норм
и правил.
На
рис. 16 показана оптимизация прогиба
простой балочной фермы с помощью
изменения площадей сечений стержней.
Синим цветом показана зависимость
прогиба при изменяющихся значениях
коэффициентов
 ,
,
 ,
,
 .
Красным цветом представлена зависимость
прогиба при постоянных значениях
коэффициентов. Таким образом, наглядно
можно увидеть, что изменение жесткости
системы позволяет уменьшить прогиб
конструкции.
.
Красным цветом представлена зависимость
прогиба при постоянных значениях
коэффициентов. Таким образом, наглядно
можно увидеть, что изменение жесткости
системы позволяет уменьшить прогиб
конструкции.

Рис. 16 - Зависимость прогиба от коэффициентов изменения площади сечений соответствующих групп стержней. ( – при вертикальных стрежнях, – раскосы).

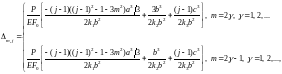 где
где
