6. Сложное сопротивление.
6.1. Расчет внецентренно сжатой колонны.
Задача 10.
Колонна заданного поперечного сечения сжимается расчетной силой F, направленной параллельно продольной оси и приложенной к точке, показанной на сечении.
Расчетные сопротивления для материала колонны:
на растяжение R=1,4 МПа;- на сжатие Rcж=22 МПа.
Требуется:
1) найти положение нейтральной (нулевой) линии;
2) вычислить наибольшие сжимающие и растягивающие напряжения, построить эпюру напряжений, дать заключение о прочности колонны;
3) построить ядро сечения.
Таблица 10.
№ п/п |
Нагрузка F, кH |
Размеры сечения, см |
Точка приложения силы |
|
а |
b |
|||
1 |
100 |
20 |
14 |
3 |
2 |
280 |
26 |
12 |
1 |
3 |
440 |
36 |
22 |
2 |
4 |
120 |
22 |
18 |
2 |
5 |
300 |
30 |
24 |
3 |
6 |
460 |
30 |
28 |
1 |
7 |
140 |
26 |
24 |
3 |
8 |
320 |
24 |
28 |
1 |
9 |
480 |
42 |
28 |
2 |
10 |
220 |
24 |
18 |
3 |
6.1.1. Пример решения задачи 10.
Колонна заданного поперечного сечения сжимается расчетной силой F, направленной параллельно продольной оси и приложенной к точке, показанной на сечении.
Расчетные сопротивления для материала колонны:
на растяжение R=1,4 МПа;- на сжатие Rcж=22 МПа.
Требуется:
1) найти положение нейтральной (нулевой) линии;
2) вычислить наибольшие сжимающие и растягивающие напряжения, построить эпюру напряжений, дать заключение о прочности колонны;
3) построить
ядро сечения.
F=80 кН;
a=20 см;
b=12 см. Рис. 6.1. Схема поперечного сечения колонны
Рис. 6.2. Положение центра тяжести и нулевой линии. Эпюра напряжений.
Решение.
Определим координаты
тяжести сечения. Поперечное сечение
колонны имеет ось симметрии
,
следовательно, центр тяжести лежит на
этой оси и для отыскания координаты
относительно вспомогательной оси ОХ
, сложное
сечение разбиваем на три прямоугольника.
где
,
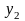и
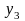- координаты центров тяжести прямоугольников
относительно вспомогательной оси ОХ,
а
,
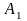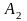и
- площади их поперечных сечений.
Определим геометрические характеристики сечения. Для вычисления главных центральных моментов инерции воспользуемся зависимостью между моментами инерции при параллельном переносе осей.
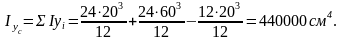
Определим квадраты радиусов инерции:
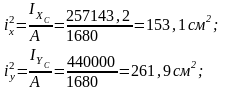
Координаты точки приложения силы F:
xF = -10 см, yF = - 7,7 см.
Положение нулевой линии:
По найденным отрезкам, отсекаемых на осях координат, проводим нулевую линию (рис 6.2).
Определим наибольшие сжимающие и растягивающие напряжения. Наиболее удаленными от нулевой линии точками являются точки А и В. Их координаты:
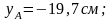
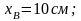
Напряжения в этих точках определяются по формуле:
Знак минус перед формулой показывает, что сила, приложенная к колонне, является сжимающей.
Нулевая линия делит сечение на зоны сжатия (область приложения силы F) и растяжения.
Растягивающее напряжение:
Сжимающие напряжение:
Прочность колонны
обеспечена.
По результатам
расчета напряжений
и
строим эпюру
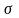(рис. 6.2). Построим ядро сечения (рис.
6.3).
Чтобы получить очертание ядра сечения, необходимо рассмотреть все возможные положения касательных к контуру сечения и, предполагая, что эти касательные являются нулевыми линиями, вычислить координаты граничных точек ядра относительно главных центральных осей сечения. Соединяя затем эти точки, получим очертание ядра сечения.
Касательная 1-1:
;
;
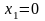Рис. 6.3. Ядро сечения.
Касательная 2-2:
;
.
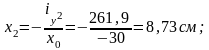
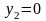Касательная 3-3:
Определим координаты точек пересечения касательной 3-3:
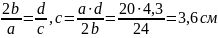
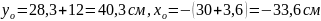
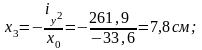
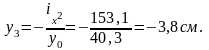
Касательная 4-4:
;
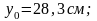
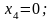
Поскольку сечение имеет ось симметрии , то все определенные координаты переносим симметрично этой оси (рис. 6.3).