5.1.1. Примеры решения задачи 8.

Пример 1.

Неразрезная балка нагружена расчетной нагрузкой. Материал балки - сталь с расчетными сопротивлениями R=210 МПа; R_c=130 МПа и модулем продольной упругости E=200 ГПa, F=4 кН, q= 3 кН/м, а=2 м.

Требуется:

1. построить эпюру поперечных сил и изгибающих моментов;

2. подобрать сечение из прокатного двутавра;

3. определить прогибы на концах и посередине каждого пролета балки и показать очертание ее изогнутой оси (использовать любой из известных методов определения прогибов).

Рис. 5.1. Схема балки, основная система, грузовая и единичная эпюры

Решение.

Данная схема имеет одну избыточную связь, т. е. балка один раз статически неопределима. Для образования основной системы отбросим шарнирную опору В и приложим в этом сечении неизвестную силу Х₁ = Y_В (рис. 5.1,б).

Построим эпюру изгибающих моментов (М_F ) в основной системе (рис. 5.1,в), определив опорные реакции:

∑ М_А = 0; F8a -Y_с 7а+ q4a2a=0;

416-Y_с 14+384=0; Y_с = 11,43 кН;

∑ М_с = 0; Y_А 7а- q4a5a+ Fa =0;

Y_А 72-34252+42=0; Y_А = 16,57 кН;

∑Y = 0; Y_А + Y_с - F - q4a = 0; 16,57+11,43-4-38 = 0;

М_А = 0; М_В = Y_А 4а - q4a2a = 16,578-384=36,56 кНм;

М_с = Y_А 7а - q4a5a = 16,5714-3810= -8 кНм.

Приложим в точке В вместо отброшенной связи силу Х₁ = 1 и построим единичную эпюру (М₁) (рис. 5.1,г).

Определим повторно опорные реакции от единичной нагрузки:

∑ М_А = 0; -Y_с 7а-14a=0; -Y_с 14-8=0; Y_с = 0,57 кН;

∑ М_с = 0; Y_А 7а+13a=0; Y_А 14+6=0; Y_А = 0,43кН;

∑Y = 0; -0,57-0,43+1 = 0;

М_А = 0 кНм; М_В =-0,438=-3,44 кНм; М_с = 0 кНм;

Запишем каноническое уравнение метода сил:

₁₁х₁ + _1F =0.

Для определения коэффициента и грузовой составляющей уравнения перемножаем грузовую (М_F) и единичную (М₁) эпюры с использованием правила Верещагина. Предварительно разделим грузовую эпюру на простые фрагменты (рис. 5.1,в).

Рассчитаем глубину параболы:

f= = = 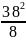24 кНм;

₁₁ = = ( ) = = ;

_1F = = =

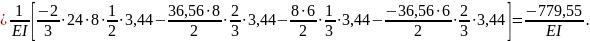
Решаем каноническое уравнение и определяем величину момента Х₁ :

=0; Х₁ = 14,11 кНм;

Производим расчет основной системы с учетом нагрузки и найденной силы Х₁ (рис. 5.2).

Определим опорные реакции:

∑ М_А = 0; F8a -Y_с 7а+ q4a2a-Y_B4a=0;

416-Y_с 14+384-14,118=0; Y_с = 3,37 кН;

∑ М_с = 0; Y_А 7а- q4a5a+ Y_B3a+Fa =0;

Y_А 72-34252+14,116+42=0; Y_А = 10,52 кН;

∑Y = 0; Y_А + Y_с + Y_B - F - q4a = 0; = 0; 10,52+3,37+14,11-38-4=0

Построим эпюры поперечных сил и изгибающих моментов (рис. 5.2,б и 5.2,в):

Q_A=10,52 кН; Q_В(л)= 10,52-38=-13,48 кН;

Q_В(п)= -13,48+14,11=0,63 кН; Q_С(л)=0,63 кН;

Q_С(п)=0,63+3,37=4 кН;

М_A= 0 кНм; М_В= 10,528-384=11,48 кНм;

М_С=10,5214-3810+14,116=-8 кНм; М_D= 0 кНм;

Z_k = 3,5 м; М_к=10,523,5-33,5 =18,45 кНм.

Рис.5.2. Эпюра поперечных сил и изгибающих моментов

в исходной схеме балки

Произведем кинематическую проверку правильности решения. Для этого перемножаем конечную эпюру М на единичную М₁ .

v_B = =

;

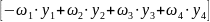Ошибка: , что допустимо.

Прогиб в сечении В равен нулю, что соответствует условию ее деформации. Подберем сечение балки из условия:

_max = R; W_x =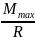 = =87,9 см³;

Из таблицы (Приложение 1) выбираем двутавр №16 с W_x =109 см³, I_x=873 см⁴.

Определим прогибы в сечениях балки и построим упругую линию. Приложим единичные силы посреди пролетов и на конце балки, построим единичные эпюры изгибающих моментов на каждом из участков, рассматривая их отдельно (рис. 5.3).

Участок АВ (рис.5.3,а):

Предварительно разделим грузовую эпюру на простые фрагменты. Определим значения изгибающего момента посредине пролета (z=4м): М_(z=4)= Y_А 2а- q2aa=10,524-342=-18,08 кНм;

Рассчитаем глубину параболы:

f= = = 6 кНм;

Перемножим грузовую и единичную эпюры:

v_N = =

.

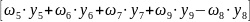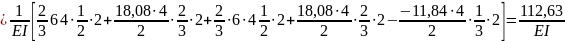Участок ВС (рис.5.3,б):

Определим изгибающий момент посредине пролета:

М_(z=3)= кНм

( на участке АВ эпюра изгибающих моментов линейная).

Рис. 5.3. Грузовые и единичные эпюры на участках АВ, ВС и ВD.

Эпюра прогибов балки.

Перемножим грузовую и единичную эпюры:

v_L = =

.

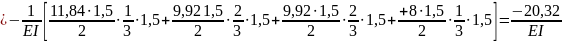Знак «минус» показывает, что направление прогиба обратно действию единичной силы.

Участок СD (рис.5.3,в):

Приложим единичную силу в точке D и построим единичный момент. Перемножим грузовую и единичную эпюры:

V_D = =

;

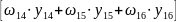Построим эпюру прогибов балки (рис. 5.3,г):

V_N = 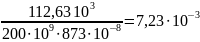м=7,23 мм.

V_L = 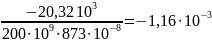м= -1,16 мм.

V_D = м=3,8 мм.

Пример 2.

Балка нагружена расчетной нагрузкой. Материал балки – сталь с расчетным сопротивлением R=210 МПа, R_с=130 МПа, и модулем продольной упругости Е=200 ГПа, q= 12 кН/м, m=6 кНм, а=1 м.

Требуется: