ИДЗ Вариант 7

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА АВТОМАТИЗИРОВАННЫХ СИСТЕМ УПРАВЛЕНИЯ

ИДЗ

«Доказательство принадлежности к NP классу»

по дисциплине

«Математическая логика»

Студент

Ельшаева Н.

подпись, дата

фамилия, инициалы

Группа

АС-09

Принял

Гаев Л.В.

ученая степень, звание

подпись, дата

фамилия, инициалы

Липецк 2010

1.Задание

Доказать принадлежность к NP класcу выбранной задачи.

ВАРИАНТ 7. НАИМЕНЬШИЙ ПО МОЩНОСТИ КЛЮЧ

УСЛОВИЕ. Заданы множество "имен атрибутов" А, семейство F упорядоченных пар подмножеств из А (называемых "функ­циональными зависимостями" на А) и положительное целое число М.

ВОПРОС. Существует ли для реляционной системы <A, F> ключ мощности не более М? Иначе говоря, существует ли такое под­множество К  А, что |K| ≤ M и упорядоченная пара (К, А) принадлежит "замыканию" F* семейства F? (Замыкание F* се­мейства F определяется следующим образом:

(1) F  F*,

(2) из того что В  С  A, следует, что (С, В)  F*,

(3) из того что (B, С), (В, D)  F*, следует, что (C, D)  F*, и

(4) из того, что (В, С), (В, D)  F*, следует, что (В, C U D)  F*.)

2.Доказательство принадлежности к NP классу

Представим условие данной задачи в виде входной цепочки для недетерминированной машины Тьюринга:

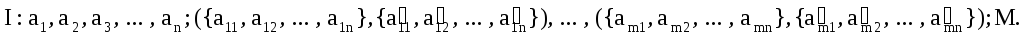
Цепочку для проверки можно представить в виде:

S : ȧ1, ȧ2, ȧ3, ... ȧn.

Алгоритм проверки цепочки S:

1. Проверить, что КА (n^2)

2. Посчитать |K| и проверить |K| ≤ M (n+1)

3. Проверить , что F  F* (4*n^2)

4. Проверить , что В  С  A (2*n^2)

5. Проверить , что (С, В)  F* (4*n^2)

6. Проверить , что (B, С), (В, D)  F* (8*n^2)

7. Проверить , что (C, D)  F* (4*n^2)

8. Проверить , что (В, С), (В, D)  F* (8*n^2)

9. Проверить , что (В, C U D)  F* (4*n^2)

10. Проверить, что (К, А) принадлежит "замыканию" F* (4*n^2)

Общее время проверки (41*(n^2)+ n+1)

Время полиноминально, следовательно задача принадлежит к NP-классу.