Основные правила обращения с кванторами

Имеется два квантора: квантор существования - , квантор общности -

Если Р(х) - некоторая высказывательная форма с единственной свободной переменной x, то возможно построение высказываний с ограниченными кванторами и неограниченными. Неограниченный квантор имеет вид:х Р(х),х Р(х). Ограниченные кванторы предполагают наличие ограничений на свободную переменную:хSР(х),хSР(х).

При работе с кванторами также выполняются законы Де моргана:

 (_x Р(х)) = _x Р(х)

 (_x Р(х)) = _x Р(х)

ПРИМЕР:

Записать не используя знаков отрицания, то что функция f(x) разрывна в точке Х₀

(_{ 0} _{ 0} хх-х₀f(x)-f(x₀))

применяется закон Де Моргана:

_{ 0} _{ 0} х(х-х₀f(x)-f(x₀))

(аb)=(аVb)=а(b)

_{ 0} _{ 0} хх-х₀f(x)-f(x₀)

Техника доказательств:

f:RRf(x)=2x

ПРИМЕР 1:

доказать, что _х,уRf(x+y)=f(x)+f(y)

доказательство: возьмем любые два вещественных числа х и у, тогда

f(x+y)=f(x)+f(y)

ПРИМЕР 2:

доказать единственность нейтрального элемента в группе А по умножению (А*х). Предположим, что имеется два различных нейтральных элемента, левосторонний eи правостороннийe’, т.е. :

х ех=х (1)

х е’х=х (2)

Поскольку формула (1) справедлива для любого х, то возьмём в качестве х значение е’ (х=е’), получим ее’=е’. Поскольку формула (2) справедлива для любого х, то возьмём х равный е, получим ее’=е

теорема: существуют два иррациональных числа а и b, такие что а^bявляется рациональным числом.

Доказательство: а=b=с=- может быть либо рациональным, либо иррациональным. Если с – рационально то теорема доказана. Если с – иррационально, о возьмём в качестве а=,b=, огда а^b=. Теорема доказана.

АЛГЕБРА ЛОГИКИ. ЛОГИЧЕСКИЕ ОПЕРАЦИИ И ОПЕРАЦИИ НА МНОЖЕСТВАХ

Одноместным предикатом на множестве А называется функция, отображающая множество А{0,1}. ПустьX- некоторое подмножество А, определяем_х: А{0,1}

_х(а)=

_хназывается характеристической функцией подмножестваX.

Операции над множествами и одноместными предикатами:

Пусть f,gотображают А{0,1}. Определим операции над функциямиfиg: А{0,1}.

(fvg)(a)=f(a)Vg(a). Аналогично fg и g

Две постоянные функции: 0: А{0,1}

1: А{0,1}

0(а)=0, 1(а)=1

Теорема: Пусть X,Y, тогда:

_х V _Y = _xy

_х  _Y = _xy

 _x = _x

0=_Ø, 1=_A

доказательство: пусть аА

(_хV_Y)(a)= _х(a)V _Y(a)=

То есть первое тождество доказано, а второе аналогично. Теперь рассмотрим третье тождество:

(_х)(a)=(_х)(a)=

_x (a)=

Четвёртое аналогично.

Следствие:Пусть имеется логическое тождество в которое входят только операции,V,. Тогда если вместо переменных подставить имена подмножеств множества А и заменить логические операции операциями над множеством:,,, а константы 0,1 на пустое множество и множество А, то получится верное тождество для множеств.

Лекция 13

Операции над подмножествами и одноместными предикатами

Пусть отображение fиg- одноместные предикаты; определим следующие операции над ними:

1.

2.

3. ;

4. - тождественно равно 0 на А;

5. - тождественно равно 1 на А;

Теорема:

Пусть X и Y – два произвольных подмножества множества А, тогда:

1. ;

2. ;

3. , где;

4. ;

5. ;

Доказательство:

Рассмотрим произвольное :

===

2. Рассмотрим произвольное :

===

3.

Следствие:

Пусть имеется булево тождество, в которое входят только связки ,,

, тогда, если вместо переменных подставить произвольные подмножества множества А и заменитьна, а 0 и 1 наи А, то получится верное равенство.

Операция - исключающее или.

Для множеств XиYопределяется операция “симметрическая разность”. На самом деле операциянад предикатами соответствует операциинад множествами.

Булевы функции

Определение:

БФ от nпеременных– это отображение.

Теорема:

Каждую БФ можно выразить через операцию ,,.

Доказательство:

Пусть f:{0,1}ⁿ {0,1} – БФ отnпеременных

1) Если (x₁,x₂,…,x_n){0,1}ⁿ f(x₁…x_n)=0,тоf(x₁…x_n)=x₁(x₁)

2) Пусть функция fтождественно

Рассмотрим ,x{0,1}. Обозначимx^=

Для любого набора (₁,₂,…,_n), для которого функцияfпринимает значение 1, мы рассмотрим выражение вида:

x₁^1x₂^2…x_n^n

Дизъюнкция всех этих выражений даёт булеву функцию f

Докажем это: S={(₁…_n){0,1}ⁿ|f(₁…_n)=1 }

Тогда g(x₁…x_n) = (x₁^1x₂^2…x_n^n)

g(x₁…x_n)=f(x₁…x_n)

Определим, при каких значениях x₁…x_n функцияg=1(₁…_n)S,такой чтоX₁^1Х₂^2…Х_n^n=1

X₁^1Х₂^2…Х_n^n=1_i Х_i=_i.

Т.е. g(x₁…x_n)=1 для тех наборов, которые входят в множестваS.

С другой стороны, f(x₁…x_n)=1 только для тех, которые входят в множествоS.

Т.е. функции fиgпринимают значения 1 и 0 на одних и тех же наборахf=g.

Следствие:

Каждую БФ можно выразить, используя только 2 операции: или

Замечание:

Представленная в теореме функция gназывается совершенной дизъюнктивной нормальной формой (СДНФ). Исходя из тождества=xстроится совершенная конъюнктивная нормальная форма. Возьмём СДНФ:

Тогда ¬=(¬)=

=

Пусть ρ(x₁…x_n)=f(x₁…x_n), тогда ρ(x₁…x_n)=

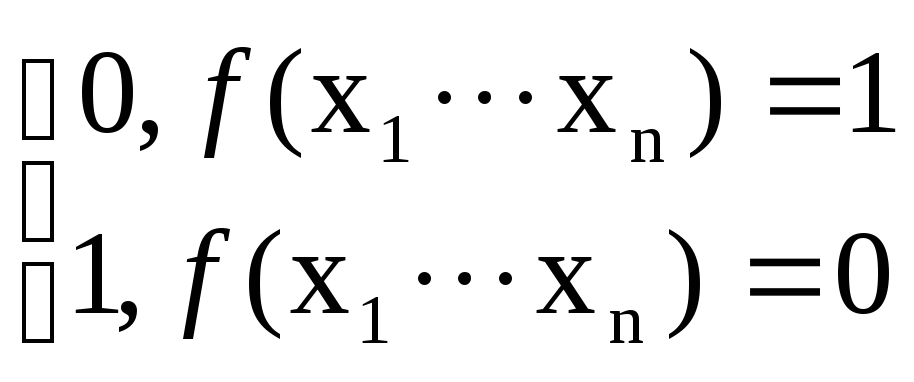
ρ(x₁…x_n)=

f=-(ρ(x₁…x_n))=()=