5.1.4. Решение игр в смешанных стратегиях

Если игра не имеет седловой точки, то применение чистых стратегий не дает оптимального решения игры. Так, в задаче №1 ,седловая точка отсутствует. В таком случае можно полу­чить оптимальное решение, случайным образом чередуя чистые стратегии.

Смешанной стратегией S_A игрокаАназывается применение чистых стратегийА₁, А₂,…, А_i,…, А_mс вероятностямиp₁, р₂,…,p_i, ..., p_т, причем сумма вероятностей равна 1:. Смешанные стратегии игрокаАзаписываются в виде матрицы

или в виде строки S_A = (p₁, р₂,…,p_i, ..., p_т).Аналогично смешан­ные стратегии игрокаВобозначаются:

где сумма вероятностей появления стратегий равна 1:

Чистые стратегии можно считать частным случаем смешанных и задавать строкой, в которой 1соответствует чистой стратегии. На основании принципа минимакса определяетсяоптимальное решение(илирешение)игры: это пара оптимальных стратегийS^*_A, S^*_Bв общем случае смешанных, обладающих следующим свойством: если один из игроков придерживается своей опти­мальной стратегии, то другому не может быть выгодно отступать от своей. Выигрыш, соответствующий оптимальному решению, называется ценой игры v.Цена игры удовлетворяет неравенству:

(5.1.4.1)

где и —нижняя и верхняя цены игры.

Справедлива следующая основная теорема теории игр — тео­рема Неймана.Каждая конечная игра имеет по крайней мере одно оптимальное решение, возможно, среди смешанных стратегий.

Пусть S^*_A = (p^*₁, р^*₂,…, p_т) иS^*_B = (q^*₁, q^*₂,…,q^*_n) — пара опти­мальных стратегий. Если чистая стратегия входит в оптимальную смешанную стратегию с отличной от нуля вероятностью, то она называетсяактивной.

Справедлива теорема об активных стратегиях:если один из игро­ков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равным цене игры v,если второй игрок не выходит за пределы своих активных стратегий.

Эта теорема имеет большое практическое значение —она дает конкретные модели нахождения оптимальных стратегий при от­сутствии седловой точки.

Рассмотрим игру размера 2 х 2,которая является простейшим случаем конечной игры. Если такая игра имеет седловую точку, то оптимальное решение —это пара чистых стратегий, соответст­вующих этой точке.

Игра, в которой отсутствует седловая точка, в соответствии с основной теоремой теории игр оптимальное решение существует и определяется парой смешанных стратегий S^*_A = (p^*₁, р^*₂) и S^*_B = (q^*₁, q^*₂).

Для того чтобы их найти, воспользуемся теоремой об активных стратегиях. Если игрок Апридерживается своей оптимальной стратегииS^*_A,то его средний выигрыш будет равен цене игры v, какой бы активной стратегией ни пользовался игрокВ.Для игры 2х2любая чистая стратегия противника является активной, если отсутствует седловая точка. Выигрыш игрокаА(проигрыш игрокаВ) —случайная величина, математическое ожидание (среднее значение) которой является ценой игры. Поэтому средний выиг­рыш игрокаА(оптимальная стратегия) будет равенvи для 1-й, и для 2-й стратегии противника.

Пусть игра задана платежной матрицей

Средний выигрыш игрока А, если он использует оптимальную смешанную стратегию 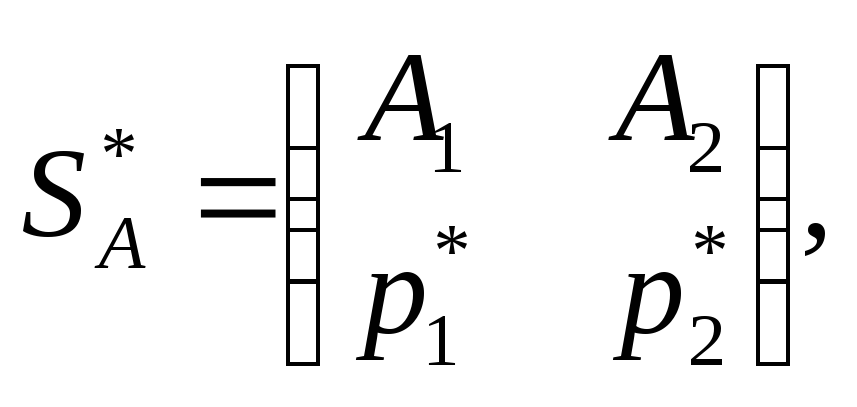а игрок В — чистую стратегию B₁ (это соответствует 1-му столбцу платежной матрицы Р), равен цене игры v:

Тот же средний выигрыш получает игрок А, если 2-й игрок применяет стратегиюВ₂, т.е.а₁₂р^*₁ +а₂₂р^*₂ =v. Учитывая, чтор^*₁ +р^*₂ =1, получаем систему уравнений для определения опти­мальной стратегииS^*_Aи цены игры v:

(5.1.4.2)

Решая эту систему, получим оптимальную стратегию

(5.1.4.3)

и цену игры

(5.1.4.4)

Применяя теорему об активных стратегиях при отыскании S^*_B —оптимальной стратегии игрокаВ,получаем, что при любой чистой стратегии игрокаА (А₁илиА₂)средний проигрыш игрокаВравен цене игры v,т.е.

(5.1.4.5)

Тогда оптимальная стратегия S^*_B = (q^*₁, q^*₂) определяется формулами:

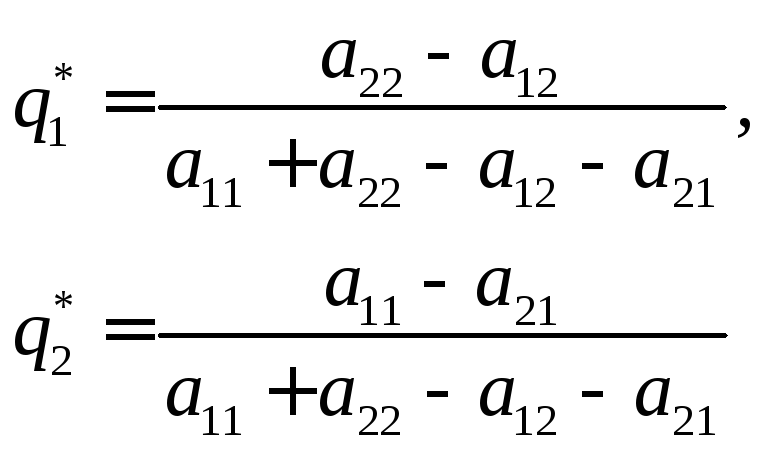(5.1.4.6)

Применим полученные результаты для отыскания оптималь­ных стратегий для игры, рассмотренной в примере 5.1.3.1.

Пример 5.1.4.1. Найти оптимальные стратегии игры, приведенной в примере 5.1.3.1.

Решение.Игра "поиск" задана платежной матрицей без седловой точки:

Поэтому ищем решение в смешанных стратегиях; для игрока А средний выигрыш равен цене игры v(приВ₁иВ₂); для игрокаВ средний проигрыш равен цене игры v(приА₁иА₂). Системы уравнений (6)и (9)в данном случае имеют вид:

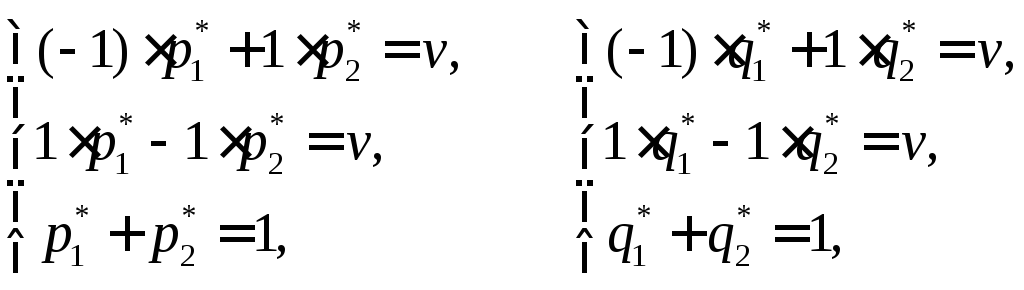
Решая эти системы, получаем p^*₁=p^*₂= q^*₁= q^*₂= 1 / 2,v = 0.

Это означает, что оптимальная стратегия каждого игрока со­стоит в том, чтобы чередовать свои чистые стратегии случайным образом, выбирая каждое из убежищ с вероятностью 1/2,при этом средний выигрыш равен 0.