
- •Симплекс-метод.
- •2.1. Основные операции и теоремы линейного программирования
- •Понятие о симплекс-методе
- •Алгоритм симплекс-метода
- •2.4. Вырожденность в задачах линейного программирования. Проблема зацикливания
- •2.4.1.Симплекс метод (метод последовательного улучшения плана)
- •2.4.2.Алгоритм симплекс метода
- •2.4.3.Построение оптимального плана.
- •2.4.4.Построение опорного плана.
- •2.4.5Правила выбора разрешающего элемента при поиске опорного плана.
- •2.4.6.Вырожденность в задачах линейного программирования
- •2.5. Анализ линейных моделей на чувствительность. Двойственный симплекс-метод.
- •2.6. Использование искусственной переменной в программировании симплекс-методом.
- •2.7. Модифицированный симплекс - метод
- •2.7.1. Теоретические сведения
- •2.7.2. Мультипликативное представление обратной матрицы
- •2.7.3.Алгоритм модифицированного симплекс-метода.
- •2.7.4.Выводы
- •2.8. Целочисленное линейное программирование (зцлп)
- •Методы решения зцлп
- •Метод ветвей и границ
2.4.4.Построение опорного плана.
Пусть необходимо решить задачу:
![]() (2.10)
(2.10)
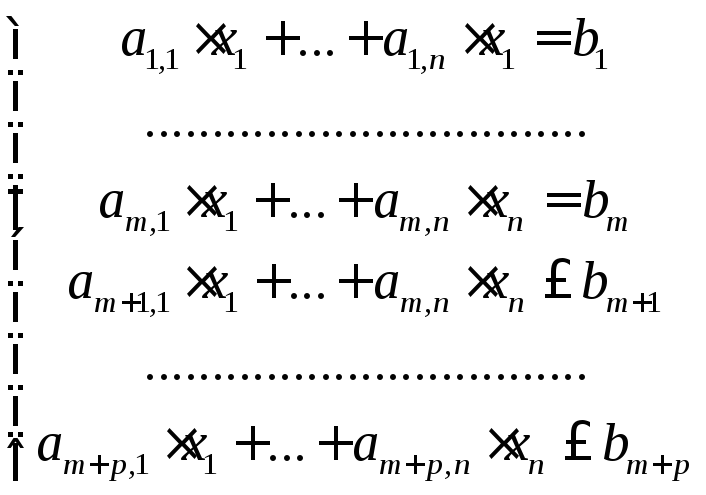 .
(2.11)
.
(2.11)
Введем дополнительные переменные, чтобы преобразовать ограничения-неравенства к равенствам. В ограничениях-равенствах дополнительные переменные должны быть нулевыми. Тогда система ограничений принимает вид:
 ,
(2.12)
,
(2.12)
где xn + i≥ 0,i= 1, ...,p.
В качестве базисных переменных будем брать систему дополнительно введенных переменных. Тогда симплексная таблица для преобразованной задачи будет иметь следующий вид:
Таблица 2.14
|
|
-x1 |
-x2 |
…. |
-xs |
.… |
-xn |
1 |
|
0 |
a1,1 |
a1,2 |
…. |
a1,s |
…. |
a1,n |
b1 |
|
…. |
…. |
…. |
…. |
…. |
…. |
…. |
…. |
|
0 |
am,1 |
am,2 |
…. |
am,s |
…. |
am,n |
bm |
|
xm+1 |
am+1,1 |
am+1,2 |
…. |
am+1,s |
…. |
am+1,n |
bm+1 |
|
…. |
…. |
…. |
…. |
…. |
…. |
…. |
…. |
|
xm+p |
am+p,1 |
am+p,2 |
…. |
am+p,s |
…. |
am+p,n |
bm+p |
|
|
-c1 |
-c2 |
…. |
-cs |
…. |
-cn |
0 |
2.4.5Правила выбора разрешающего элемента при поиске опорного плана.
При условии отсутствия "0-строк" (ограничений-равенств) и "свободных" переменных (т.е. переменных, на которые не наложено требование неотрицательности).
Если в столбце свободных членов симплексной таблицы нет отрицательных элементов, то опорный план найден.
Есть отрицательные элементы в столбце свободных членов, например bi< 0. В такой строке ищем отрицательный коэффициентail, и этим самым определяем разрешающий столбецl. Если не найдем отрицательныйail,то система ограничений несовместна(противоречива).
В качестве разрешающей выбираем строку, которой соответствует минимальное отношение:
 ,
(2.13)
,
(2.13)
где r- номер разрешающей строки. Таким образом,arl- разрешающий элемент.
После того, как разрешающий элемент найден, делаем шаг модифицированного жорданова исключения с направляющим элементом arlи переходим к следующей симплексной таблице.
В случае присутствия ограничений-равенств и "свободных" переменных поступают следующим образом.
Выбирают разрешающий элемент в "0-строке" и делают шаг модифицированного жорданова исключения, после чего вычеркивают этот разрешающий столбец. Данную последовательность действий продолжают до тех пор, пока в симплексной таблице остается хотя бы одна "0-строка" (при этом таблица сокращается).
Если же присутствуют и свободные переменные, то необходимо данные переменные сделать базисными. И после того, как свободная переменная станет базисной, в процессе определения разрешающего элемента при поиске опорного и оптимального планов данная строка не учитывается (но преобразуется).
2.4.6.Вырожденность в задачах линейного программирования
Рассматривая симплекс-метод, мы
предполагали, что задача линейного
программирования является невырожденной,
т.е. каждый опорный план содержит ровно
mположительных компонент, гдеm– число ограничений в задаче. В вырожденном
опорном плане число положительных
компонент оказывается меньше числа
ограничений: некоторые базисные
переменные, соответствующие данному
опорному плану, принимают нулевые
значения. Используя геометрическую
интерпретацию для простейшего случая,
к огдаn - m= 2 (число небазисных переменных
равно 2), легко отличить вырожденную
задачу от невырожденной. В вырожденной
задаче в одной вершине многогранника
условий пересекается более двух прямых,
описываемых уравнениями видаxi= 0. Это значит, что одна или несколько
сторон многоугольника условий стягиваются
в точку.
огдаn - m= 2 (число небазисных переменных
равно 2), легко отличить вырожденную
задачу от невырожденной. В вырожденной
задаче в одной вершине многогранника
условий пересекается более двух прямых,
описываемых уравнениями видаxi= 0. Это значит, что одна или несколько
сторон многоугольника условий стягиваются
в точку.
Рис. 2.3
Аналогично при n - m= 3 в вырожденной задаче в одной вершине пересекается более 3-х плоскостейxi= 0.
В предположении о невырожденности задачи находилось только одно значение
 ,
(2.14)
,
(2.14)
по которому определялся индекс выводимого из базиса вектора условий (выводимой из числа базисных переменной). В вырожденной задаче
 (2.15)
(2.15)
может достигаться на нескольких индексах сразу (для нескольких строк). В этом случае в находимом опорном плане несколько базисных переменных будут нулевыми.
Если задача линейного программирования оказывается вырожденной, то при плохом выборе вектора условий, выводимого из базиса, может возникнуть бесконечное движение по базисам одного и того же опорного плана. Так называемое, явление зацикливания. Хотя в практических задачах линейного программирования зацикливание явление крайне редкое, возможность его не исключена.
Задача называется невырожденной задачей, если ранг матрицы А равен m и любой опорный план является невырожденным планом. Если хотя бы один опорный план является вырожденным в задаче, то задача называется вырожденной. Поясним понятие вырожденности на примерах.
Пример 2.9:
. -5х1+ х2+ х3 -2x4- х5 -> min
|
2x1 +6х3 +4х4- Зх5 =2, |
|
-х1+3х2+7х3 -2X5=1, |
|
Х1+ х2+ 2х3 +х4+ 2х5 =1,xi >= 0, i=l,..,5; |
Пример 2.10:
. -x1-3x2-2 х3 -4х4- х5->min
|
-x1 +4х3 +3х4 =2, |
|
2х1+3х2+ Зх3 +5х4 -х5=1, |
|
x1+3x2+ х3 +2x4+ х5 =2, хi>0, 1=1,..,5; i=l,..,5; |
Для задачи примера 2.9 опорным
является, например, план х=(1/5, 2/5, О, 2/5,
0), поскольку столбцы  матрицы ограничений соответствующие
положительным координатам вектора х,
линейно независимы. Этот опорный план
невырожден, так как число положительных
координат вектора х равно 3 – числу
строк матрицы ограничений.
матрицы ограничений соответствующие
положительным координатам вектора х,
линейно независимы. Этот опорный план
невырожден, так как число положительных
координат вектора х равно 3 – числу
строк матрицы ограничений.
Для задачи примера 4.3 вектор х=(3/4, 0, 11/16, 0, 9/16) является невырожденным опорным планом, а план х=(0, 1/2, 1/2, 0, 0) вырожден.
Один из приемов борьбы с вырожденностью состоит в преобразовании задачи путем "незначительного" изменения вектора правых частей системы ограничений на величины εi, таким образом, чтобы задача стала невырожденной, и, в то же время, чтобы это изменение не повлияло реально на оптимальный план задачи.
Чаще реализуемые алгоритмы включают в себя некоторые простые правила, снижающие вероятность возникновения зацикливания или его преодоления.
Пусть переменную xjнеобходимо сделать базисной. Рассмотрим множество индексовE0, состоящее из техi, для которых достигается
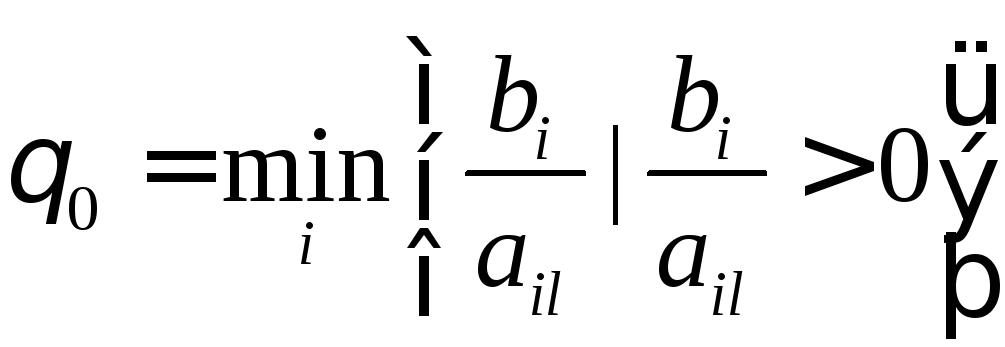 .
(2.16)
.
(2.16)
Множество индексов i, для которых
выполняется данное условие обозначим
черезE0. ЕслиE0состоит из одного элемента, то из базиса
исключается вектор условийAi(переменнаяxiделается
небазисной). ЕслиE0состоит
более чем из одного элемента, то
составляется множествоE1,
которое состоит из![]() ,
на которых достигается
,
на которых достигается
 .
(2.17)
.
(2.17)
Если E1состоит из одного индексаk, то из базиса выводится переменнаяxk. В противном случае составляется множествоE2и т.д.
Практически правилом надо пользоваться, если зацикливание уже обнаружено.
